10. Краткий кугс лекций1 семестр 1 лекция 1. Множества. Операции над множествами

Множество в математике является основным, неопределяемым понятием, т.е. таким поня­тием, которое не может быть определено через другие понятия. Так как определения понятия «множество» не существует, то смысл его поясняется на примерах. Примерами множеств могут служить множество столов в кабинете, множество деревьев в парке, множество студентов в университете, множество окон в доме, множество букв в слове.

Из приведенных примеров становится ясно, что под множеством понимается совокупность объектов какой-либо природы. Множества обозначают прописными буквами латин­ского алфавита: А, В, С,..., X, Y, Z. За некоторыми множествами закреплены специальные обозначения: N, Z, Q, R (множества натуральных, целых, рациональных, действительных чисел соот­ветственно),  (пустое множество), I (универсальное множество) и т.д.

Элементами множества называются те объекты, из которых оно состоит. Элементы множества обозначаются строч­ными буквами латинского алфавита: а, b, с,..., х, у, z. Если объект а является элементом множества А, то говорят, что а принадле­жит множеству А, и пишут: а А. В противном случае говорят, что а не принадлежит множеству А, и пишут: а  А. Например, тот факт, что число 5 является натуральным, записывают так: 5N. А то, что число 0,5 не натуральное, запишется следующим образом: 0,5N.

Множества могут состоять из элементов, которые сами являются множествами. Например, множество факультетов вуза, множество рабочих бригад в организации и т.д.

Множества бывают конечные и бесконечные. К ко­нечным множествам относятся, например, множество дней неде­ли, множество карандашей в коробке и т.д. Примерами же бес­конечных множеств могут служить множества N, Z и некоторые другие.

Пустым множеством называется множество_, не со­держащее ни одного элемента. В качестве примеров пустых множеств можно привести множество согласных букв в слове «ау», множество ног у «колобка» и т.д.

Считают, что множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или нет.

Существует два способа задания множеств:

1. перечисление элементов,

2. указание характеристического свойства элементов.

Способом перечисления обычно задаются конечные множества, состоящие из небольшого числа элементов. Но ино­гда этим способом задают и бесконечные множества, перечислив некоторые из их элементов. Для задания множества способом перечисления их элементы (все, в случае конечных множеств, или часть их, в случае бесконечных множеств) записывают через запятые и заключают в фигурные скобки.

ПРИМЕР 1. Зададим некоторые множества спосо­бом перечисления:

А = {а, b, с}, В = {{а, b}, с}, С - {ива, береза, рябина}, D = {5,10}, N={1, 2, 3,...}, N₂ = {2, 4, 6,... }, Z = {0, ± 1, 2,...}.

Здесь множества А, В, С, D - конечные множества, а множества N, N2, Z - бесконечные.

Указанием характеристического свойства можно за­давать в равной мере как конечные, так и бесконечные множества.

Характеристическим свойством элементов данного множества называется свойство, которым обладают все элемен­ты данного множества и не обладает ни один объект, не принад­лежащий данному множеству.

Если произвольное характеристическое свойство обозна­чить Р(х), то множество, элементы которого обладают этим свойст­вом, обозначается так: {х |Р (х)}. Читается это обозначение следую­щим образом: множество всех х, таких, что х обладает свойством Р. Т.е. вертикальная черта в записи {х |Р(х)} заменяет слова «таких, что».

ПРИМЕР 2. Множество А = {1, 2, 3, 4, 5} можно задать вторым способом так. А = {х /х  N, х 5 }. Множество N₂ из примера 1 задается указанием характеристического свой­ства следующим образом: N2 = {х /х  N, х- четное}. Множе­ство квадратов можно задать так: К = {х /х - прямоугольник с равными сторонами}.

ОПРЕДЕЛЕНИЕ 1. Множество В называется подмножеством множества А, если каждый элемент множества В принадлежит и множеству А.

Если В является подмножеством множества А, то пишут: В  А (либо A  В). Запись В  А можно прочитать и так: В включается в А, В содержится в А и т.д.

Принято считать, что пустое множество является под­множеством любого множества. Кроме того, из определения 1 сле­дует, что любое множество является своим подмножеством. Пустое множество и само множество называют несобственными подмножест­вами данного множества. Остальные подмножества данного множест­ва, если они существуют, называют собственными.

ПРИМЕР 3. Подсчитаем число подмножеств сле­дующих множеств: , А ={5}, В = {a, b}.

Подмножеством пустого множества является только пустое множество, то есть число подмножеств пустого множест­ва N=1.

Подмножествами множества А являются множества  и {5},, то есть для множества А число подмножеств N = 2.

Подмножествами множества В являются множества , {a}, {b}, {a, b}. Видим, что в этом случае N = 4 = 2².

Из приведенного примера можно сделать следующий вывод.

Если множество А состоит из т элементов (записы­вается это так: п(А) = т, то число всех подмножеств N множест­ва А вычисляется по формуле:

N = 2^m. (1)

Отметим, что отношение включения множеств наря­ду со свойством А А, называемым рефлексивностью включе­ния, обладает еще и свойством транзитивности (определения по­нятий «отношение», «рефлексивность», «транзитивность» смот­рите в лекции «Соответствия. Отношения»).

Универсальным множеством называется множество, со­держащее в себе все множества, рассматриваемые в данной задаче. Не существует абсолютно универсального множества. Множество, являющееся универсальным в данной задаче, может в другой задаче оказаться подмножеством какого-либо множества. На­пример, в задаче, где рассматриваются множества треугольников, ту­поугольных треугольников, остроугольных треугольников, прямо­угольных треугольников, равнобедренных треугольников, равносторонних треугольников, естественно в качестве универсального множе­ства взять множество треугольников. Если же, кроме перечисленных множеств, рассматривать еще и множество многоугольников, то ясно, что универсальным будет последнее множество.

ОПРЕДЕЛЕНИЕ 2. Равными множествами назы­ваются множества, состоящие из одних и тех же элементов.

Если множества А и В равны, то пишут А = В.

Из определения 2 вытекает следующий критерий равенства множеств.

Два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.

Для наглядного изображения множеств чертят круги Эйлера - круги или близкие к ним фигуры, точки которых изо­бражают элементы множеств. Изображение различных множеств с учетом отношений между ними называют диаграммами Эйлера-Венна. На диаграммах Эйлера-Венна универсальное множество принято обозначать в виде прямоугольника:

ОПРЕДЕЛЕНИЕ 3. Пересечением множеств А и В называется множество, состоящее из всех элементов, при­надлежащих обоим множествам А и В.

Обозначение пересечения множеств А и В следующее: АВ. Таким образом, по определению, АВ ={х  х  А и х  В}. Если это пересечение не пусто, то говорят, что множест­ва А и В пересекаются. В противном случае, т.е. при АВ = , говорят, что А и В не пересекаются.

Операцию нахождения пересечения множеств на­зывают также пересечением. Операция пересечения множество обладает следующими свойствами:

1) A =,

2)АА=А,

3. коммутативность: АВ=ВА,

4. ассоциативность: А  (ВС) = (АВ)С,

5) АВ тогда и только тогда, когда АВ=А,

6)АI=А.

ОПРЕДЕЛЕНИЕ 4. Объединением множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В.

Объединение множеств А и В обозначают: АВ. Таким образом, по определению 4, АВ={х  х А или х В}.

ПРИМЕР 4. Найдем пересечение и объединение множеств А = {1,2,3,4,5} и В = {5,1, 3, 6, 8,10}.

АВ = {1,3, 5}, АВ = {1, 2, 3, 4, 5, 6, 8,10}.

Операцию нахождения объединения множеств на­зывают также объединением. Операция объединения множеств обладает следующими свойствами:

1)А =A,
2) А  А =А,
3) коммутативность: А  В =В  А,
4) ассоциативность:
А (ВС) = (АВ) С=АВС,
5) закон поглощения:
А В тогда и только тогда, когда АВ=В,
6) AI=I.

Свойства 3) - 5) операций пересечения и объединения распространяются и на произвольное конечное число множеств.

Свойства, связывающие операции пересече­ния и объединения:

7)А (ВА)=А,

8)А(ВА)=А,

9. дистрибутивность объединения относительно пересечения:

А(ВС) = (А  В)  (А  С),

9. дистрибутивность пересечения относительно объединения:

А  (В С) = (А  В)  (А  С).

Свойства 9), 10) доказываются с опорой на опреде­ления пересечения, объединения, подмножества и на теорему о равенстве множеств.

Докажем 10). В силу критерия равенства множеств достаточно доказать, что

a) A(ВС) (АВ)(АС),

б) (АВ)(АС A (ВС).

Докажем а). Пусть х A(ВС). Это, по опреде­лению пересечения, означает, что хА и хВС. Из хВС сле­дует, в силу определения объединения, что хВ или хС. Если х  В, то хАВ и, следовательно, х (АВ)(АС). Если же хС, то х А С, из чего следует, что х(АВ)(АС). Утверждение а) доказано.

Докажем б). Пусть х (АВ)(АС). Из этого следует, в сипу определения объединения, что х АВ или х  А С. Если х АВ, то, по определению пересечения хА и хВ, то есть, с учетом определения объединения, хА и хВС. Применяя опреде­ление пересечения, получаем, что х A(ВС). Если же х  А С, тo хА и х С, из чего следует, что хА и хВС. Из по­следнего получаем, что х A(ВС). Утверждение б) дока­зано. Из а) и б) следует 10).

Справедливость свойств 1) - 10) операций пересече­ния и объединения можно наглядно проиллюстрировать на диа­граммах Эйлера-Венна. Для этого надо построить диаграммы Эйлера-Венна отдельно для левой и правой частей равенств в 1) -10) и сравнить области, изображающие эти части. Они должны быть одинаковы.

Для примера проиллюстрируем 10):

На диаграмме слева область с двойной штриховкой изображает множество, находящееся в левой части равенства 10). На диаграмме справа область с двойной, горизонтальной и вертикальной штриховками изображает множество, находящееся в правой части равенства 10). Формы областей одинаковы, наглядно показывает справедливость равенства 10).

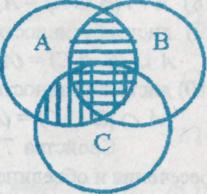
ОПРЕДЕЛЕНИЕ 5. Разностью множеств А и В называется множество, состоящее из всех элементов, принадле­жащих множеству А, но не принадлежащих множеству В.

Разность множеств А и В обозначается: А \ В. Таким образом, по определению, А \ В = {ххA и xB}.

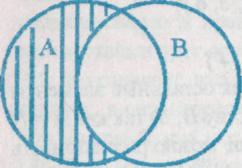
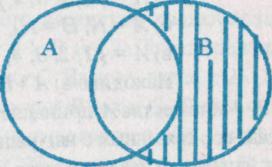
На диаграмме Эйлера-Венна слева заштрихованная область изображает разность А \ В, справа- разность В\ А.

ОПРЕДЕЛЕНИЕ 6. Дополнением множества А называется разность между универсальным множеством I и множеством А.

Дополнение множества А обозначается: А^/. Таким образом, по определению, А^/ = I \ А. Если множество, до ко­торого рассматривается дополнение данного множества, не является универсальным, то это обозначается так. А_В^/ (читается: до­полнение множества А до множества В).

ПРИМЕР 5. Найдем разность множеств А \ В в случаях:

а)А={1,2,3>4},В = {2,3,4,5,6},

б)A=N,B = N2

в) А = {1, 2, 3, 4, 5, 6}, В = {3, 4}

Находим: а) А \ В = {1}, так как остальные элементы 2, 3, 4 множества А принадлежат и множеству В.

б) Так как А = N в задачах, связанных с натуральными числами, можно рассматривать как универсальное множество, то здесь ищем N₂^’. N₂^’= {1, 3, 5, 7,...}.

в) Здесь ВА, поэтому А\В =B^/_A= {1, 2, 5, 6}.

Операции нахождения разности множеств и допол­нения называют вычитанием. Но чаще всего за ними оставляют названия «разность» и «дополнение».

Операции разности и дополнения, обладают следую­щими свойствами:

1)А\В=А, при АВ=,

2.  ^/=I,

3)I^/ = ,

4)А \ В =, при AB,

5) А \ =А,
6) А'А=1,
7) А'А=,
8) (А/)/=А,
9) А\(ВС) = (А\В)(А\С),
10)А \ (В С) = (А \B)(A\C) =(A\ B) \ С,
11)А\ (В\С) = (А \ В) С, если СА,
12) (АВ)/=А/В/,
13) (АВ)/= А/В/,
14) А \ В = А  В/,
15) (А \ В)  В =А, если В  А,
16) AB = (A\(A В))  В.

ОПРЕДЕЛЕНИЕ 7. Декартовым произведением множеств А и В называется множество всех упорядоченных пар, первая компонента которых принадлежит множеству А, а вторая - множеству В.

Декартово произведение множеств А и В обозначают: АВ. По определению АВ = {(х,у) | xА, xВ}.

Считается, что упорядоченные пары (х, у) и (z, t) равны, если х = z, у = t.

ПРИМЕР 6. Найдем декартово произведение множеств А = {1, 2, 3} и В = {а, b}:

АВ = {(1, а), (1, b), (2, а), (2,b),(3,а),(3,b)}.

Операцию нахождения декартова произведения множеств называют декартовым умножением, но чаще в литера­туре встречается название «декартово произведение».

Операция декартова произведения множеств не под­чиняется ни коммутативному, ни ассоциативному законам.

Операция декартова произведения обладает свойст­вом дистрибутивности (слева и справа) относительно операций объединения, пересечения и разности множеств.

ОПРЕДЕЛЕНИЕ 8. Декартовым произведением множеств А₁, А₂,…., А_n называется множество всех упорядочен­ных наборов вида (а₁, а₂,..., a_n), первая компонента которых при­надлежит множеству А₁, вторая - множеству А₂,..., п - я- множе­ству А_n.

Каждый такой набор называется кортежем. Номер последней компоненты называется длиной кортежа. Кор­тежи (а₁, а₂,..., a_n) и (b₁, b₂,..., b_m) считаются равными, если они имеют одинаковую длину, то есть п = т, и каждая компонента первого кортежа равна компоненте второго кортежа с тем же номером, то есть а₁ = b₁, а₂ = b₂,,..., a_n = b_m..

Декартово произведение множеств А₁, А₂,…., А_n обо­значается А₁ А₂….А_n .

Декартово произведение двух числовых множеств можно геометрически иллюстрировать, изображая его элементы точками на координатной плоскости.

Для того, чтобы изобразить декартово произведение числовых множеств А и В, нужно изобразить множество А на оси абсцисс, множество В - на оси ординат. Затем изобразить на координатной плоскости все точки, абсциссы которых принад­лежат множеству А, а ординаты - множеству В. Полученная фи­гура, состоящая из конечного либо бесконечного числа точек, и будет представлять наглядно декартово произведение множеств А и В.

Заметим, что вся координатная плоскость представ­ляет собой изображение декартова произведения RR, которое также называют декартовым квадратом R и обозначают R².