0. Численное решение с помощью Excel задачи построения оптимального портфеля (задача г.Марковица - общий случай)

В качестве численного примера рассмотрим решение задачи для случая трех ценных бумаг с параметрами своего варианта.

См. варианты_инв_курс_пр.xls, лист2

Портфель состоит из 3х независимых ценных бумаг, и описываться следующими уравнениями:

x₁+x₂+x₃=1 (уравнение баланса); (2.9)

m=m₁ x₁+ m₂ x₂+ m₃ x₃ (уравнение дохода) (2.10)

При этом риск портфеля будет равен:

(уравнение риска) (2.11),

где x_1, x₂, x₃ - доля средств, потраченных на приобретение 1, 2 и 3-ей ценной бумаги,

m_i - средняя доходность i-ой ценной бумаги (математическое ожидание эффективности i-ой ценной бумаги) i=1,2,3,

- риск i-ой ценной бумаги (дисперсия эффективности i-ой ценной бумаги) i=1,2,3,

Задача Г.Марковица в этом случае имеет вид. Найти структуру x_1, x₂, x₃ портфеля ценных бумаг, обеспечивающую минимальный риск (2.7), при выполнении линейных ограничений: уравнения баланса (2.9) и фиксации доходности (2.10). Определить риск оптимального портфеля инвестора.

Для своего варианта

• Численными методами произвести расчет оптимального портфеля инвестора с помощью программы оптимизации Excel «Поиск решения ». Рассмотреть несколько вариантов доходности портфеля. Определить риск оптимального портфеля инвестора

• Определить структуру x_1, x₂, x₃ и риск 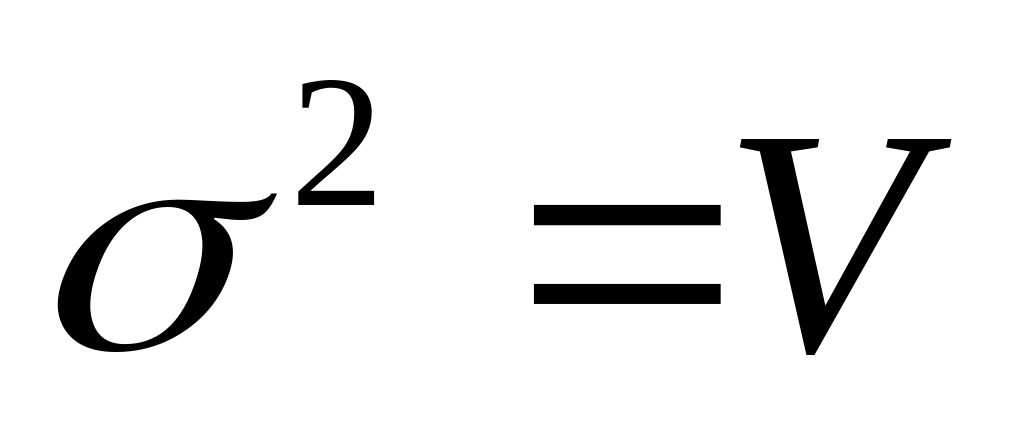оптимального портфеля инвестора для четырех - восьми значений доходности m портфеля из вашего варианта

• Построить графики зависимости структуры x_1, x₂, x₃ и риска портфеля от доходности m оптимального портфеля.

• Рассмотреть случай, когда дополнительно используются ограничения (2.4) в виде неравенств 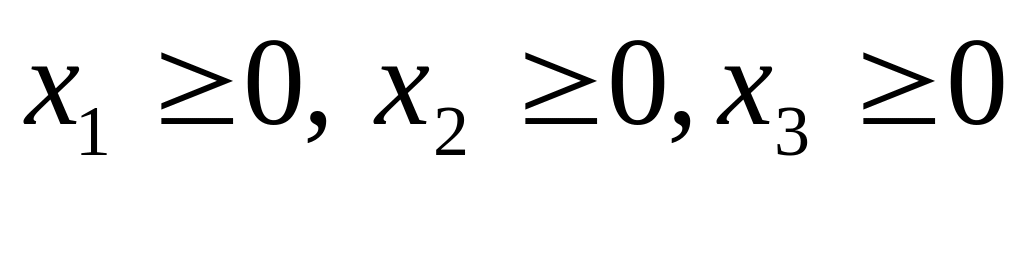. Определить риск и структуру оптимального портфеля.

• Построить графики зависимости структуры x_1, x₂, x₃ и риска портфеля от доходности m оптимального портфеля для случая когда .

• На основании полученных результатов сделать выводы о свойствах оптимального портфеля в задаче Г.Марковица.

См. инвестиции_курс_пр.xls, лист4

См. Optimal.exe

3. Построение оптимального портфеля ценных бумаг при рискованных и безрисковых вложениях. Задача д.Тобина (j.Tobin).

0. Постановка задачи.

Ценные бумаги, входящие в портфель инвестора, можно разделить условно на две группы. В первую группу войдут ценные бумаги, имеющие малый риск и умеренную доходность. Во вторую группу войдут ценные бумаги, имеющие большую доходность и соответственно больший риск. Бумаги, имеющие малую доходность и больший риск, очевидно, не следует включать в портфель.

К безрисковым ценным бумагам можно отнести государственные ценные бумаги. В частности, на рынке США это вексель казначейства (US Treasury Bill), расписки казначейства (US Treasury Notes), бона казначейства (US Treasury bonds).

Тобин Д. рассмотрел следующую предельную ситуацию, когда инвестор выделяет х₀ денег на приобретение государственных ценных бумаг с ожидаемой доходностью г₀ и нулевым риском. Остальные 1-х₀ денег инвестор тратит на рискованные ценные бумаги, например акции, с ожидаемой доходностью m_i большей, чем эффективность безрисковых бумаг г₀, т. е. m_i>r₀ (i=1,2,...,n).

Математическая постановка задачи следующая.

Требуется найти распределение средств инвестора х₀, x₁, х₂..., х_п между безрисковыми и рискованными бумагами 1, 2,..., п такое, что выполняются линейные ограничения:

х₀ + х_] + х₂ +... + х_п = 1 (уравнение баланса) (3.1)

m_ох_о + m₁х₁ + m₂х₂ +... + m_пх_п = m_s (3.2)

(фиксация ожидаемой суммарной доходности портфеля акций на уровне т_s)

и минимизируется риск, равный

V=v₁₁x₁²+v₂₂x₂²+...+v_nnx_n²+2(v₁₂x₁x₂+v₁₃x₁x₃+…+v_n-1,n x _n-1x_n), (3.3)

где - риск i-ой ценной бумаги (дисперсия эффективности i-ой ценной бумаги) i=1,2,…n.,

- ковариация i-ой и j–ой ценной бумаги, определяющая связь между эффективностями i-ой и j–ой ценной бумагой i=1,2,…n, j =1,2,…n.