Білет №19

1. Загальна характеристика кодерів загортальних кодів

2. Потенційна перешкодостійкість двійкового каналу зв’язку, критерій ідеального спостерігача

Відповіді

Кодери згортальних кодів.

Визначення. Лінійний постійний у часі деревоподібний ( , )- код, що має кінцеву довжину слова , називається згортальним ( , )- кодом. Згортальний ( , )- код, що задовольняє умові систематичності, називається систематичним згортальним ( , )- кодом.

Помітимо, що ми можемо називати той самий код деревоподібним ( , )- кодом або згортальним ( , )- кодом.

Рис. 2. Приклади згортальних кодерів.

На рис. 2 показані приклади кодерів для двох різних згортальних кодів для випадку і . Перший з них служить кодером для систематичного двійкового ( ) згортального (12, 6)- коду з довжиною кодового обмеження, рівного , другий є кодером для несистематичного двійкового згортального (6, 3)- коду з довжиною кодового обмеження .

В обох випадках вхідні символи перетворяться двома фільтрами (КІХ- фільтрами – з кінцевою імпульсною характеристикою), один із яких утвориться верхніми відводами, а іншої – нижніми. Символи з виходів цих двох фільтрів поперемінно в часі зчитуються і подаються в буфер по одному символі в одиницю часу з кожного виходу; їхнє зчитування з буфера виробляється вдвічі частіше, ніж надходять вхідні символи.

Відомо кілька способів опису роботи згортальних кодерів. Обговоримо їх більш докладно.

Згортальний кодер, як кінцевий автомат з пам'яттю, може бути описаний діаграмою станів. Можливі станів кодеру описуються при і символами (рис.2, б), тобто кодер може знаходитися в одному з 4-х можливих станів = 00, 01, 10, 11, причому стан характеризує останній інформаційний символ. Діаграма станів являє собою спрямованого графа, що містить усі стани і можливі переходи з одного стану в інше, описувані виходами кодеру (кодовими символами кадру). Діаграма станів приведена на рис. 3.

У кружках зазначені стани кодеру ( ), стрільцями – можливі переходи. Біля стрілок показані символи на виході кодеру ( ), що відповідають кожному переходові.

К одер працює в такий спосіб. Спочатку він знаходиться в стані «00» і при надходженні на вхід символу «0» на вихід кодеру видаються символи = 00. Наступний запис вхідного символу «0» у переводить його також у стан «00». На діаграмі цей перехід позначений петлею «00» біля стану «00». Далі, при надходженні на вхід символу «1» на виході кодеру формуються кадр кодових символів «11» з наступним переходом кодеру в стан «10». Цей перехід зі стану «00» у стан «10» позначається стрілкою, супроводжуваної кодом «11», і т.д.  Побудова діаграми закінчується, коли переглянуті всі можливі переходи з кожного стану в усі інші. Процес формування діаграми рис. 3 розглянемо на прикладі.

Задача 1. Побудувати діаграму функціонування згортального (6, 3)-коду.

Рішення.

Подамо на вхід згортального кодера рис. 2, б інформаційну послідовність (тут як і колись молодші розряди ліворуч). Процес формування діаграми функціонування згортального (6, 3)- коду наочно ілюструє табл.1.

Таблиця 1

Такт						Вхід кодера	Состояния кодера		Виходи кодера
	u0	u1	u2	u3	u4	S0	S1	S2	c1	c2
	1	1	1	0	1		0	0	0	0
1		1	1	1	0	1	0	0	1	1
2			1	1	1	0	1	0	1	0
3				1	1	1	0	1	0	0
4					1	1	1	0	0	1
5						1	1	1	1	0
6							1	1	0	1
7							0	1	1	1
8							0	0	0	0

Розгорнення станів у часі утворить, так звану, решітчасту діаграму (рис. 4) (звідси назва – решітчасті коди), на якій стани показані вузлами, а переходи – з'єднуючими їхніми лініями, супроводжуваними значеннями символів ( ) кодового слова.

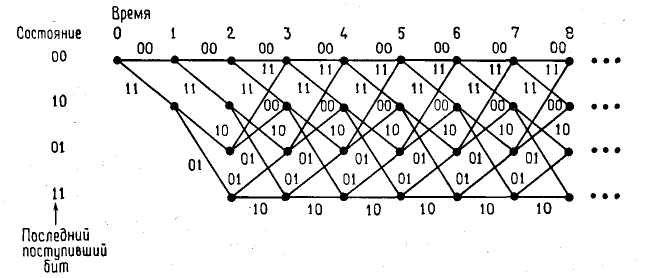
Рис. 4. Решітчаста діаграма згортального (6, 3)-коду.

Решітчаста діаграма – граф, вузли якого знаходяться в прямокутній координатній сітці, напівнескінченної праворуч; число вузлів у кожнім стовпці кінцево. Конфігурація ребер, що з'єднують вузли кожного стовпця з вузлами стовпця праворуч, однакова для всіх стовпців. Вузли, що не можуть бути досягнуті при русі вправо з верхнього лівого вузла, звичайно не вказуються.

Вузли в кожному стовпці решітки представляють станів, у яких може знаходитися регістр зсуву. Кожен наступний стовпець решітки являє собою набір станів у наступний момент часу.

Надходження на вхід нового інформаційного кадру приводить до зміни стану регістра зсуву, що відповідає ребру, що веде до наступного вузла. У розглянутому прикладі кожне ребро позначене двома двійковими символами, переданими в канал при переході в наступний стан регістра зсуву. Тут ведуча з довільного вузла верхня пряма відповідає нульовому вхідному двійковому символові, а нижня – одиничному. У загальному ж випадку кожне ребро позначається вихідними символами, що йому відповідають.

Маркірована решітка описує згортальний код у тім смислі, що всі шляхи від вузла до вузла ліворуч праворуч по решітці позначають кодові слова. Маркірування ребер однакове для кожного сегмента (часового кадру) і лінійна в тім смислі, що лінійна комбінація маркірувань будь-якої безлічі ребер є маркіруванням деякого ребра.

Помітимо, що решітка може бути маркірована і при інших обмеженнях (див. розглянуті вище властивості) або при їхній повній відсутності. Якщо маркірування не має властивість лінійності, то, як ми уже вказували, код називається ковзним блоковим кодом. Якщо маркірування міняється від кадру до кадру, то такий код відомий під загальною назвою решітчастого коду. Нарешті, якщо число станів у наступних друг за другом часових кадрах продовжує необмежено рости, те такий код називається загальним деревоподібним кодом.

Задача 2. Використовуючи решітчасту діаграму рис. 4, визначити кодову послідовність на виході згортального кодера рис. 2, б при подачі на його вхід інформаційної послідовності виду .

Рішення.

Решітчаста діаграма зображує всі дозволені шляхи, по яких може просуватися кодер при кодуванні. Жирною лінією на рис.5 показаний шлях по решітці 1110000110, що відповідають надходженню на вхід кодера інформаційної послідовності 1 0 1 1 1. Відповідно галузям решітчастої діаграми в міру просування одержуємо кодові посилки 11.10.00.01.10... і т.д.

Білет №20

1. Декодування загортальних кодів. Алгоритм Вітербі.

2. Характеристика послуг безпеки відповідно до стандарту.

Відповіді

1. Декодування згортальних кодів. Алгоритм Вітербі.

Для декодування згортальних кодів найбільше широко застосовується алгоритм декодування Вітербі (алгоритм максимальної правдоподібності).

Алгоритм декодування Вітербі є повним алгоритмом декодування згортальних кодів, у зв'язку з чим імовірність відмовлення від декодування дорівнює нулеві. Однак при фіксованому коді імовірність помилки декодування буде більше, ніж у неповного декодера. Цей алгоритм практично може бути використаний для двійкових кодів з малою довжиною кодового обмеження — у даний час межею є довжини кодового обмеження від 7 до 10. Нижче описується процедура, що являє собою процес декодування по мінімуму відстані від шляху, що генерує кодер.

3.1. Декодування в умовах відсутності помилок у каналі.

Алгоритм Вітербі має ряд переваг перед іншими, у зв'язку з чим його широко використовують для декодування коротких згортальних кодів. Розглянемо особливості алгоритму на прикладі декодування коду, породжуваного кодером рис. 2, б, зі швидкістю . З дискретного двійкового каналу у виді послідовності кадрів кодових символів (тут номер кадру ( ) і номер кроку декодування) на вхід декодера надходять кодові посилки – 00.00.11.01.10.01.11.00.00.11.10.00.01.01.11.00. Функціонування декодера (як і кодера) описується процесом «розвитку» решітчастої діаграми, що ілюструється на рис. 9. Тут кружками показані стани кодера (декодера), усередині яких поміщені значення так званих метрик станів , ліворуч приведені слова-стани кодера ( ), у дужках поруч – інформаційні символи (значення ), що відповідають вихідний (декодованої) послідовності, а під колонками станів зазначені кроки декодування.

«Розвиток» діаграми для кодерів зі швидкістю завжди відбувається за 3 кроки. У початковий момент часу (крок 0) декодер знаходиться в стані «00» і вихідна метрика станів – .

З рисунка видно, що з кожного стану декодера до кожного нового стану веде дві гілки (див. також діаграму станів рис. 3). У процесі «розвитку» решітчастої діаграми до нового стану вибирається тільки одна гілка.

Номер кроку: 0 1 2 3

Рис. 9. Процес «розвитку» решітчастій діаграми при декодуванні

Вихідні з вихідного стану «00» гілки (позначені на рисунку кодами і власне на лініях, що зображує гілки) ведуть відповідно до станів «00» і «10». Для кожної з цих гілок необхідно обчислити так називану метрику гілки (на рисунку позначається кодом над гілкою). Метрика гілки дорівнює відстані Хемминга між кадром символів на вході декодера (на рисунку позначені жирним шрифтом у верхній частині діаграми) і набором символів , що відповідають даній гілці на решітчастій діаграмі (рис. 9), тобто числу розрядів, значеннями яких вони відрізняються –

, .

Так, наприклад, при для гілки, що веде в стан «00», метрика дорівнює , а для гілки, що веде в стан «10», – .

На кожнім -м кроці декодування відповідно до алгоритму Вітербі в кожнім із станів решітчастої діаграми виробляються однотипні операції:

1) відшукання метрик вхідних шляхів додаванням метрик попередніх станів з метриками відповідних гілок;

2) порівняння метрик вхідних шляхів і вибір шляхів з найменшими метриками, величини яких використовують як метрики станів поточного кроку декодування;

3) визначення декодованого на даному -м кроці символу (у даному випадку дв. розряд) по стану кодера з мінімальною метрикою – .

У такий спосіб у загальному виді алгоритм Вітербі декодування згортальних кодів на довільному -му кроці описується наступними співвідношеннями:

, ; (3*а)

; (3*б)

по , . (3*в)

Розглянемо більш докладно зміст декількох перших кроків алгоритму Вітербі декодування приведеної вище тестової кодової послідовності.

Для перших двох кроків ( ) роботи алгоритму характерним є те, що на наступні стани замість пари гілок «спирається» тільки по одній гілці. У цих умовах метрика стану визначається як сума метрик вхідної гілки і попереднього стану .

Для 1-го кроку декодування метрики станів рівні:

;

.

Далі вибирається шлях до стану з мінімальною метрикою, у даному випадку – до стану , і отже декодований інформаційний розряд дорівнює .

На 2-м кроці декодування з урахуванням значення чергового кадру кодових символів обчислюються метрики гілок (їх уже 4) і метрики станів по співвідношенням

;

;

;

.

Як і на попередньому кроці мінімальна метрика в стану , а значить черговий відновлений інформаційний розряд дорівнює .

Зауваження. Уже на цьому кроці може скластися враження, що немає необхідності розраховувати метрики всіх можливих станів і досить обмежитися обчисленням метрик двох станів, у які ведуть шляхи зі стану з мінімальною метрикою, отриманої на попередньому кроці (у даному випадку в 1-м). Однак такий підхід виявляється можливим тільки в припущенні постійної відсутності помилок на приймаючій стороні, що в умовах наявності в каналі шумів і завад по суті є подією неможливим.

Наявність помилок породжує процес «розмноження шляхів, що вижили» і поява хоча б ще одного шляху, що «вижив», приводить до необхідності обліку метрик усіх станів, що буде показано нижче при розгляді роботи декодера Вітербі при перекручуванні в каналі кодової послідовності. Тому починаючи з 2-го кроку в алгоритмі декодування здійснюється розрахунок метрик усіх можливих станів.

Далі алгоритм складається в періодичному повторенні основного кроку, відмінною рисою якого є наявність двох шляхів до кожного наступного стану.

Роблячи попарне порівняння метрик шляхів, що входять у кожен стан, вибирають меншу метрику і неї вважають метрикою даного стану для наступного кроку декодування. Шлях, що входить у даний стан з меншою метрикою, вважають «вижившими» (на діаграмі рис. 9 шляхи, що «вижили», показані жирними лініями). Тонкою лінією показані шляхи, що відкидаються при попарному порівнянні. У результаті порівняння вибирають меншу метрику і неї вважають метрикою даного стану для наступного кроку декодування.

На 3-м (і кожнім наступному ) кроці реалізуються співвідношення (на кроці кадр кодових символів дорівнює )

;

;

;

.

На даному кроці мінімальна метрика в стану , а значить черговий відновлений інформаційний розряд дорівнює .

Далі алгоритм Вітербі повторює виконання основного кроку по співвідношеннях (3*).

Процес побудови решітчастої діаграми рис.4 для декодування послідовності виду 00.00.11.01.10.01.11.00.00.11.10.00.01.01.11.00 показаний на рис. 10.

Якщо метрики порівнюваних шляхів однакові, то вибір одного з двох шляхів роблять довільним образом. На кожнім кроці алгоритму при відсутності помилок у каналі в результаті порівняння половина можливих шляхів відкидається і надалі не використовується. Інша половина утворить продовження шляхів для наступного кроку декодування.

У такий спосіб декодер простежує по кодовій решітці шлях, що має мінімальну відстань від шляху, що генерує кодер. Недвійкові коди декодировать декодером Вітербі трудніше, і це можливо лише при дуже малих довжинах кодового обмеження.