Статистичні оцінки параметрів розподілу

Основні вимоги до статистичних оцінок.

У багатьох випадках треба дослідити кількісну ознаку X генеральної сукупності, використовуючи результати ви­бірки. Часто для цього достатньо знати наближені зна­чення математичного сподівання М(Х), дисперсію , середньоквадратичне відхилення початкові або центральні моменти випадкової величини X.

Іноді з деяких міркувань вдається встановити закон розподілу X. Тоді треба вміти оцінювати параметри цього закону розподілу.

Наприклад, відомо, що випадкова величина X розподілена рівномірно; треба по даних вибірки наближено знайти відрізок, в якому знаходяться значення випадкової величини X.

Якщо X розподілена у генеральній сукупності за нормальним законом, то її щільність імовірностей має вигляд

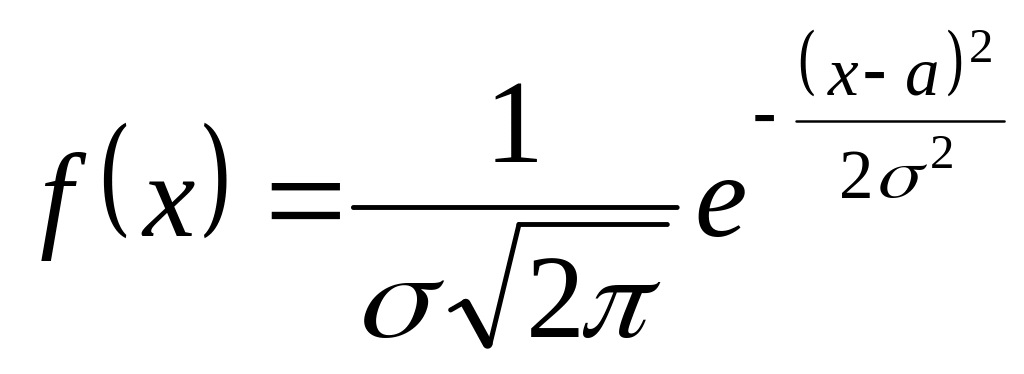
Необхідно оцінити (знайти наближені значення) параметра , який дорівнює М(Х), та . Ці параметри повністю визначають нормальний розподіл X.

Якщо X розподілена за законом Пуассона, то необхідно оцінювати лише один параметр к, яким цей розподіл визначається.

Дослідник має у своєму розпорядженні лише дані вибірки, одержані в результаті спостережень. Саме через ці дані і треба виразити потрібний параметр випадкової величини X генеральної сукупності.

Означення 1. Статистичною оцінкою невідомого параметра випадкової величини X генеральної сукупності (теоретичного розподілу X) називають функцію від випадкових величин (результатів вибірки), що спостерігаються.

Щоб статистичні оцінки давали найкращі наближення параметрів, вони повинні задовольняти певним вимогам. Розглянемо ці вимоги.

Нехай є статистична оцінка невідомого параметра в теоретичного розподілу.

Припустимо, що за вибіркою об'єму п знайдена оцінка . При інших вибірках того ж об'єму одержимо деякі інші оцінки , ..., Саме оцінку можна розглядати як випадкову величину, а числа , , ..., як її можливі значення.

Якщо числа ( =1,2,..., т) будуть більші значення , тоді оцінка дає наближене значення з надлишком. У цьому випадку математичне сподівання випадкової вели­чини буде більше , .

В іншому випадку дає оцінку з недостачею

Таким чином, використання статистичної оцінки, мате­матичне сподівання якої не дорівнює параметру в, приво­дить до систематичних (одного знака) похибок.

Вимога застерігає від систематичних похибок.

Означення 2. Статистичну оцінку параметра називають не зсунутою, якщо

Оцінку називають зсунутою, якщо ця рівність не. виконується,

Вимога про не зсунутість оцінки є недостатньою тому, що можливі значення можуть бути сильно розсіяні від свого середнього значення, дисперсія може бути великою. Тоді знайдена за даними однієї вибірки оцінка, наприклад, може набагато відрізнятись від середнього значення , отже і від параметра .

Якщо буде малою, тоді можливість допустити велику помилку буде виключена. Тому до статистичної оцінки виникає вимога про її ефективність.

Означення 3. Ефективною називають таку статистичну оцінку , яка при заданому об'єму п має найменшу можливу дисперсію.

При розгляданні вибірки великого об'єму ( ) до статистичних оцінок пред'являють вимогу їх обґрунтованості.

Означення 4. Обґрунтованою називають статистичну оцінку, яка при прямує за імовірністю до оцінюваного параметра.

Наприклад, якщо дисперсія незсунутої оцінки при прямує до нуля, то оцінка буде і обґрунтованою.

Числові характеристики вибіркової сукупності

Вибіркові характеристики

У доповнення до табличних та графічних методів представлення даних наступним найважливішим засобом обробки даних є обчислення їх числових характеристик. Най­більш важливі з них: середнє значення, дисперсія, середнє квадратичне відхилення (стандартне відхилення).

Ці характеристики можуть бути обчислені за даними, що знаходяться у вибірці або за даними, що входять у кінцеву генеральну сукупність.

Числові характеристики, обчислені по вибірці або ті, що використовуються для опису даних вибірки, називають статистиками.

Числові характеристики, обчислені по генеральній сукупності або ті, що використовуються для опису даних генеральної сукупності, називають параметрами.

Означення 1. Простою середньоарифметичною вибірки називають суму варіант вибірки, поділену на об'єм вибірки. Її позначають .

Означення 2. Вибірковою середньою або зваженою середньоарифметичною називають середню арифметичну варіант вибірки з врахуванням їх відносних частот

, .

Вибіркова середня е аналогом математичного сподівання і використовується дуже часто. Вона може приймати різні числові значення при різних вибірках однакового об'єму.