25. Циклдік кодтар. Циклдік кодтарға математикалық кіріспе.

Циклді кодтар. Кез келген екілік жүйедегі топталған кодтарды әр түрлі m жолдан тұратын n бағаналы матрицамен жазуға болады. Немесе оған керісінше кез келген п орынды кодтық қомбинациядан тұратын m жолдың жиынтығынан топталған кодтарды құрушы матрица деп қарауға болады.

Мұндай матрицаның барлык жолдарының ішінен қосымша циклдік қасиеті бар матрица құратын жолдарды бөліп шығаруға болады.

Мұндай матрицаның барлық жолдарын осы кодтың құрушы деп аталатын бір комбинациясын циклдік ығыстыру арқылы алуға болады. Осындай шартты қанағаттандыратын кодтарды циклдік кодтар деп атайды.

Ығыстыру, негізінен, оңнан солға қарай жүргізіледі. Мысалы: 0100101, 1001010,0010101, 0101010,1010100, т.е.с. Топталған әр түрлі кодтардың ішінде циклдіге жататындары көп болмайды. Сондықтан олармен берілетін мәліметтер көлемі жалпы топталған кодтармен берілетін мәліметтер көлемінен аз.

Циклді кодтарды жазғанда, оларды n дәрежесіндегі көпмүше түрінде жазу ыңғайлы.

Мысалы,

10101 -ді G(x) = 1 * х⁴ + 0 * х³ + 1 * х² + 0 * х¹ + 1 * х⁰ = х⁴ + х² + 1 деп жазуға болады.

Сөйтіп кодтық комбинациямен жасалатын жұмыс көпмүшемен жасалатын жұмысқа әкелінеді.

Кодтық комбинацияны құратын көпмүшені бір орынға ығыстырудың орнына оны х-ке көбейтеді.

Мысалы, 001101...0011010 орнына (х³ + х² + 1)х = х⁴ + х³ + х.

Осы екі комбинацияны "екілік модульмен" қосқанда алынатын комбинацияны х³ + х² + 1 көпмүшеcін (х + 1)-ге көбейтіп алуға болады.

(х³ + х² + 1) • (х + 1) = х⁴ + х² + х + 1.

Сонымен, кода құрушы көпмүшені белгілеп алғаннан кейін циклді коданың кез келген рұқсат етілген комбинациясын құрушы көпмүшені басқа бір көпмүшеге көбейту арқылы алуга болады.

Циклді кодтың кез келген көпмүшесі құрушы көпмүшеге қалдықсыз бөлінуі керек. Циклді кодтың осы қасиеті қатені табуға, ал егер қалдықсыз бөлінбесе, сол қалдықтың түріне қарап, қатенің орнын тауып түзетуге болады.

Көпмүшелерді көбейту мен бөлу кері байланысты ығыстырушы тіркегіштерде оңай орындалатын болғандықтан, циклді кодаларды қолдану өте кең тараған. Циклді код туғызушы немесе өндіруші деп аталатын мүшелерімен беріледі. Барлық мәліметті таратуға арналған көпмүшелер осы өндіруші немесе туғызушы көпмүшеге қалдықсыз бөлінуі керек.

МЫСАЛ

Циклдік кодтың тексеру матрицасы

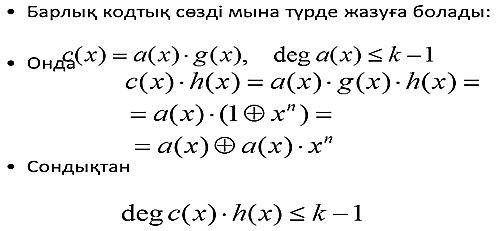
Есеп. Циклдік кодтың кодтық комбинациясын жазу керек, егер туынды полином P(x) = x³+x²+1

Ақпарат көзінен түскен кодтық комбинация – парольдің соңғы екі цифры.

шешімі:

N = 23;

23₁₀ = 10111₂

Бұл санды полином ретінде жазсақ:

A(x) = 1*x⁴+0*x³+1*x²+1*x¹+1*x⁰ = x⁴+x²+x+1

1) r=3 болсын, онда:

Екілік кодта:

A(x)*x³ = (x⁴+x²+x+1)*x³ = x⁷+x⁵+x⁴+x³

A(x) = 10111000

2) Бөлу операциясы

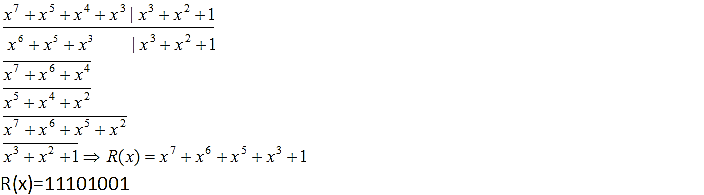
3) Кодерден өткеннен кейін сигнал мынаған тең:

26. Кедергіге төзімді кодтар және оларға қойылатын талаптар.

Байланыс арналарында қосымша элементтерді пайдалану арқылы берілетін ақпараттың дәлдігін жоғарылату үшін қолданылатын коданы kедергіге төзімді кодтар деп атайды.Кедергіге төзімді кодтар бірінші ретті кодтарға қосымша разрядтар косу арқылы жасалады. Қосымша разрядтар байланыс арналарындағы бөгеуілдердің пайда болу зандылығына байланысты қосылып, сол бөгеуілдердің әсерінен пайда болатын қателерді жою үшін пайдаланылады. Қосымша разрядтар кодтарды күрделендіреді. Дәлдікті жоғарылату дәрежесі кедергіге төзімді кодтар күрделілігіне байланысты. Дәлдікті неғұрлым жоғары дөрежеге көтеру үшін кедергіге төзімді кодтар соғұрлым күрделі болу керек. Сөйтіп акпаратты тарату дәлдігін жоғарылату әдістерінің әсері байланыс арналарындағы қателердің жалпы саны мен олардың таратылу заңдылығына байланысты болады.Егер байланыс арналарындағы қателер біріне-бірі байланыссыз, яғни корреляцияланбаған болса және бір элемент қатесінің ықтималдығы берілсе, онда қалған қателер мәліметтерін анықтау қиын емес. Тәжірибеде кездесетін байланыс арналарында кателер корреляцияланған болады. Қателердің бір түрі — қателердің топталып келуі. Мұндай топталып келетін қателерді "пакеттеліп келеді" деп те айтады. Қателер тобы немесе пакеті деп бірінші бұзылған элементтен бастап соңғы бұзылған элементке дейінгі элементтер тізбегін айтады. Осы элементтер санын пакет ұзындығы деп атайды. Екі пакет арасындағы бұзылмаған элементтер санынқорғаныс аралығы дейді. Қорғаныс аралығындағы элементтер саны пакет ұзындығынан бірнеше есе артық болу керек.Кедергіге төзімді кодтар қолданылуына жөне құрылуына байланысты бірнеше түрге бөлінеді.

• түзетуші кодалар

Екі топқа бөлінеді: Жүйеленген түзетуші кодалық топта кез келген екі кодалық комбинацияны "екілік модульмен" қосса, сол коданың үшіпші комбинациясы шығады. Жүйеленген топта ақпараттық орындарға ақпараттық символдар орналасады да, олардың белгілі бір комбинациясын "екілік модульмен" қоскан тексеруші символдар тексеруші орындарға орналасады.Жүйеленген кодалар циклденген жөне циклденбеген хэмминг кодаларына бөлінеді. Циклденген кодада символдарды белгілі бір циклмен ауыстыру арқылы келесі комбинация алынады.

Жүйеленбеген топта "екілік модульмен" қосқанда үшінші комбинация шығатын қасиет болмайды. Жүйеленбеген топта символдардың тексеру қосындылары пайдаланылады. Яғни, тексеруші символ белгілі бір ақпараттық символдардың қосындысы болады.

• жүйеленбегеп

• үзіліссіз тізбекті кодалар

Үзіліссіз немесе тізбекті кодалау кезінде кодалау және кодадан шығару үзіліссіз жүргізіледі. Мұнда түзетуші элементтер ақпараттық элементтерге тәуелді болып, сол ақпараттық элементтердің араларында орналасады.

• топталған немесе блокталған кодалар

Топталған немесе блокталған кодалау кезінде ақпараттық тізбек кодалык комбинацияларға (блоктарға немесе топтарға) бөлініп, сол топтар бөлек-бөлек кодаланып, кабылдау орнында бөлек-бөлек кодадан шығарылады.

Топталған кода екі түрде кездеседі:

• бөлінетін (ақпараттық және текесеруші символдардың әрқайсысының бөлек орындары болады)

• бөлінбейтін. (аралас орналасады)