
- •1. Жүйелер теориясы. Жүйенің қасиеттері.
- •2. Жүйе түсінігі. Жүйенің классификациясы. Жүйенің жүйелік белгілері.
- •3. Ақпараттық жүйе және құрылымы. Ақпараттық жүйелерге қойылатын талаптар.
- •4. Ақпараттық жүйелердің құрылымының жабдықтау бөлімі. Әр жабдықтауға сипаттама беру.
- •5. Классификациялау жүйесінің негізгі түсініктері. Классификациялау жүйесінің құрылымы
- •6. Ақпараттық жүйелердегі ақпаратты кодтау. Кодтау түрлері. Мысал келтіру.
- •7. Жоба туралы түсінік және жобаларды басқару. Жобалардың классификациясы. Ақпараттық жүйелерді жобалаудың негізгі әдістері.
- •8. Ақпараттық жүйелердің компоненттері. Ақпараттық жүйелердің функциялары.
- •9. Ақпараттық жүйенің өмірлік айналымы мен оның құрылымының негізгі үдерістері.
- •10. Ақпараттық жүйелердің өмірлік айналымының бірінші сатысы. Техникалық тапсырма және оның құрылымы.
- •12. Ақпараттар теориясы. Энтропия және оның қасиеттері. Хартли және Шеннон формулалары.
- •13. Ақпаратық жүйе және оның белгілері бойынша классификациясы.
- •14. Шартты энтропия және оның қасиеттері. Бірігу энтропиясы.
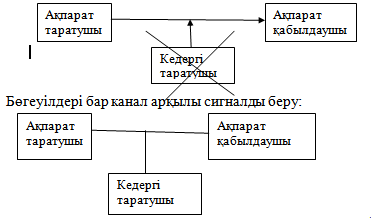
- •15. Хабарламалар және сигналдар туралы жалпы мәліметтер. Ақпараттық жүйелерде ақпаратты беру үдерісі.
- •16. Модуляция және демодуляция процедураларының қызметі мен мазмұны.
- •17. Модуляцияның әрбір түрлерінің салыстырмалы сипаттамалары.
- •18. Ақпараттық канал. Каналдың өткізу қабілеті. Канал сиымдылығының қажетті және жеткілікті шарты.
- •19. Дискретті каналдар. Котельников теоремасы.
- •20. Дискретті каналдар моделі. Дискретті каналмен ақпарат жіберу жылдамдығы.
- •21. Сигнал. Сигнал түрлері. Сигналдың көлемі.
- •22. Детерминделген сигналдардың математикалық модельдері. Ақпаратты берудің дискретті каналы.
- •1.Үзіліссіз аргументтің үзіліссіз функ 2. Үзіліссіз аргументтің дискретті функ
- •23. Хаффман ағашы. Хаффман коды. Сығу коэффициенті.
- •24. Сызықтық кодтарға математикалық кіріспе. Хэмминг шекаралары. Хэмминг коды.
- •25. Циклдік кодтар. Циклдік кодтарға математикалық кіріспе.
- •26. Кедергіге төзімді кодтар және оларға қойылатын талаптар.
- •27. Шеннон-Фано кодын құру қағидалары. Шеннон-Фано коды.
- •28. Ақпараттың құрылымдық өлшемдері: құрылымдық, геометриялық, аддитивті.
- •29. Кванттау. Уақыт бойынша дискреттеу.
- •30. Цифрлық ақпаратты сығу әдістері.
22. Детерминделген сигналдардың математикалық модельдері. Ақпаратты берудің дискретті каналы.
Сигналдар дискретті, үздіксіз және дискретті-үзіліссіз болып бөлінеді. Мұндай детерминделген сигналдардың математикалық модельдері мынадай түрлері бар:
1.Үзіліссіз аргументтің үзіліссіз функ 2. Үзіліссіз аргументтің дискретті функ
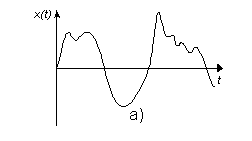
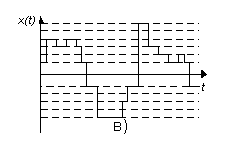
3.Дискретті аргументтің үзіліссіз функ 4. Дискретті аргументтің дискретті функ
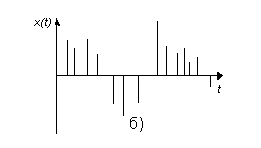
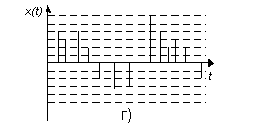
Ақпаратты берудің дискретті каналы – дискретті сигналдарды беру үшін арналған жабдықтар жиынтығы. Кедергісіз (бөгеуілсіз) каналда әрбір кіріс сигналына бір шығыс сигналы сәйкес келеді. Яғни кіріс және шығыс сигналдары бір мәнді функционалды тәуелділікпен байланысқан.
23. Хаффман ағашы. Хаффман коды. Сығу коэффициенті.
Сығу дәрежесін жақсарту үшін жиі қайталанатын символдарды қысқа кодпен, ал сирек кездесетіндерді ұзын кодпен алмастыру керек. Бүл әдіс идеясын ұсынған - Д. Хаффман (1952 жыл).
Хаффман алгоритмінің көмегімен деректерді сығу: кездесетін символдар жиілігі есептелінеді, содан кейін Хаффман кодтау ағашы тұрғызылады. Кодтау ағашы бойынша символар коды жасалынады.
Хаффман ағашын тұрғызу алгоритмі
Алғашқы символдар бос түйіндер тізімін құрайды. Әр түйіннің алғашқы хабарламадағы символдар санына тең салмағы бар.
Тізімнен ең кіші салмағы бар екі бос түйін таңдалады.
Олардың салмақтарының қосындысына тең салмағы бар «ата-ана» түйіні құрылады, ол «ұрпақтарымен» доға арқылы байланысады.
«Ата-анадан» шығатын бір доғаға 1, екіншісіне 0 қойылады.
«Ата-ана» бос түйінді тізімге қосылады, ал оның «ұрпақтары» тізімнен жойылады.
Тізімдегі қадам тек бір бос түйін қалғанша қайталана береді. Ол ағаштың басы (тамыры) болып есептелінеді.
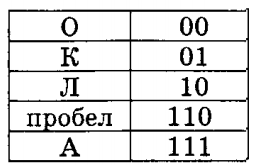
Мысалы. «КОЛ_ОКОЛО_КОЛОКОЛА» мәтіні үшін Хаффман ағашын тұрғызу және префикстік кодты алу:
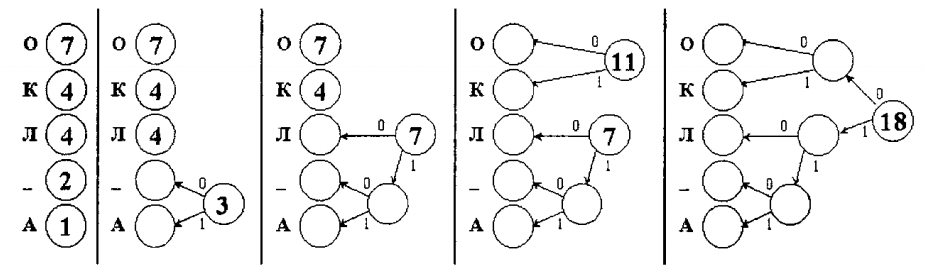
Төбелерін қоссақ, шығатыны:
3+7+11+18=39
Мәтін коды 39/бит немесе 5 байт.
Сығу коэффициенті
18/5 = 3,6.
Сығылған деректерді қалпына келтіру үшін Хаффман ағашын қолданамыз.
Хаффман коды префиксті болып табылады, себебі әр символ коды басқа символдың кодының басы болып саналмайды.
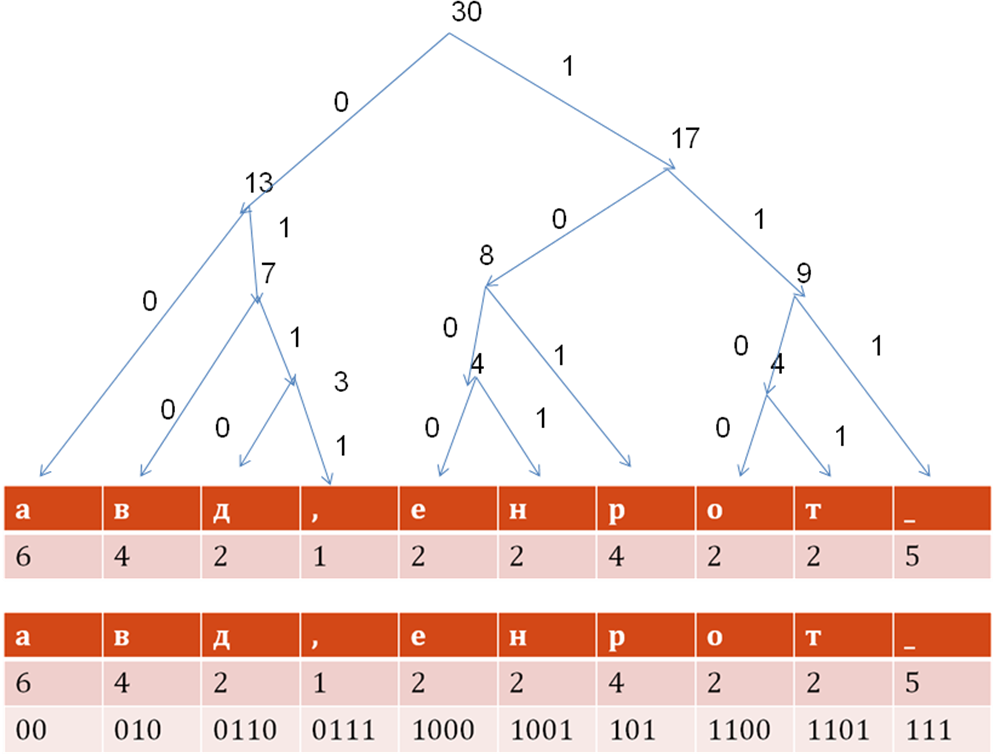
Хаффман ағашын тұрғызу: «на_дворе_трава,_на_ траве_дрова»
24. Сызықтық кодтарға математикалық кіріспе. Хэмминг шекаралары. Хэмминг коды.
Қателерді түзету кодтары 1)Блоктық 2)үзіліссіз
Блоктық кодтар

Хэмминг коды

|
Кодталған хабарламаны алайық: b28 b27 b26 b25 b24 b23 b22 B21 b20 b19 b18 b17 b16 b15 B14 b13 b12 b11 b10 b9 b8 b7 b6 b5 b4 b3 b2 b1 b1, b2, b4, b8, b16 ntrcthe тексеру разряды, ал қалғандары ақпара-қ р |
Ақпараттық разрядқа берілген кодты ретімен орналастырамыз:
b3 =1, b5 = 0, b6 = 0, b7=1,
b9=0, b10 =0, b11=0, b12=1,
b13= 1, b14=1, b15=0, b17=1,
b18=1, b19=1, b20=1, b21=0,
b22=0, b23=0, b24=0, b25=0,
b26=0, b27=0, b28=0.
Тексеру разрядының мәндері:
Ол үшін мына жиындарды енгіземіз:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… - бірінші разрядтары 1-ге тең
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… - екінші разрядтары 1-ге тең
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28… - үшінші разрядтары 1-ге тең
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28… - төртінші разрядтары 1-ге тең
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 … бесінші разрядтары 1-ге тең
b3 =1, b5 = 0, b6 = 0, b7=1,
b9=0, b10 =0, b11=0, b12=1,
b13= 1, b14=1, b15=0, b17=1,
b18=1, b19=1, b20=1, b21=0,
b22=0, b23=0, b24=0, b25=0,
b26=0, b27=0, b28=0.
Онда mod2 бойынша
b1 = b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
b2 = b3+b6+b7+b10+b11+b14+ b15+ b18+ b19+ b22+ b23+ b26+ b27 = 1
b4 = b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23+b28 = 1
b8 = b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27+b28 = 1
b16 = b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27+b28 = 0
Енді тексерк коды мен ақпараттық кодтарды біріктіреміз:
Жауабы: 1111 0011 0001 1100 1111 0000 0000.

