Метод наименьших квадратов

Пусть имеется n наблюдений (х_i, у_i), i=0, 1, 2,…, n и требуется приблизитьэти данные многочленом степени N < n:

Р_N(x)=a₀+a₁x+ a₂x²+…+ a_N x^N (5.3)

таким, который минимизирует функцию

(5.4)

Левая часть выражения (5.4) содержит независимые параметры ,

поэтому оно обозначено функцией . Согласно МНК надо найти те значения параметров (5.3), которые доставляют минимум функции

Необходимым условием минимума является равенство нулю в этой точке первых производных:

…………………. (5.5)

Для функции (5.4) эта система уравнений принимает вид:

, (5.6)

к=0, 1,…, N.

После несложных алгебраических преобразований получим систему линейных алгебраических уравнений:

…………………………………………………………… (5.7)

(5.7) является СЛАУ, определитель которой, как доказано в /5/, отличен от нуля. Значит СЛАУ (5.7) имеет единственное ненулевое решение. Из этого следует, что МНК в классе алгебраических полиномов порядка n дает единственное решение.

При N=1, т.е. при линейной аппроксимации МНК система (5.7) принимает вид:

(5.8)

Решать ее проще всего методом исключения неизвестных.

Пример. Таблично заданная функция имеет вид:

х	0 1 2 3 4
у	1 2 2,2 2,7 4,2

Нанесем эти точки на рисунок.

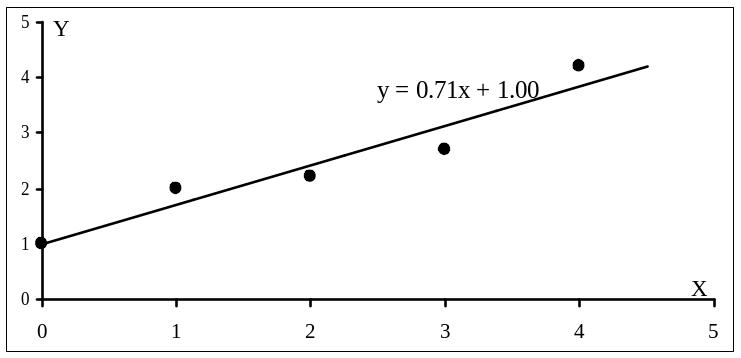
Рис6. Схема расположения точек и аппроксимирующая МНК прямая

Из расположения точек на рис.6 видно, что зависимость у=у(х) линейная, т.е. у=а₀+а₁х, отклонения значений у_i, i=0,1,…4 от этой зависимости могут быть обусловлены ошибками измерений и/или локальными неоднородностями изучаемого геологического объекта.Для нахождения линейной зависимости МНК необходимо составить систему (5.8) при N=1. Предварительные расчёты сведены в табл. 1. В этой таблице в последней строке приведены суммы значений соответствующих столбцов. По данным табл.1. составим аналог

СЛАУ (5.8):

5а₀+10а₁=12,1

10а₀+30а₁=31,3.

Таблица 1

х	у	х2	ху
1	2	3	4	5	6
0	1	0	0	1	0
1	2	1	2	1,71	0,0841
2	2,2	4	4,4	2,42	0,0484
3	2,7	9	8,1	3,13	0,1849
4	4,2	16	16,8	3,84	0,1297
10	12,1	30	31,3		0,447

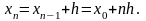
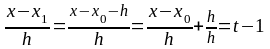
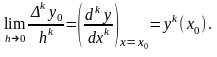
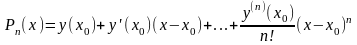
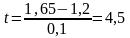
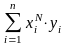
Методом исключения неизвестных находим: а₀=1, а₁=0,71, значит зависимость имеет вид у=1+0,71х. Для проверки правильности расчетов нанесем эту линию на рисунок.

Для оценки качества аппроксимации следует найти сумму квадратов отклонений замеренных значений у_i от сглаженных в заданных узлах х _i , i= 0, 1,…, 4, обозначим ее S²_ocт.

Значения находят в данном примере из выражения =1+0,71×х_i, они записаны в пятом столбце таблицы 1. По числам шестого столбца находим

S²_ocт, в данном примере S²_ocт = 0,447.