3. Упорядоченные таблицы

В упорядоченных таблицах элементы располагаются в некотором определенном порядке, задаваемым относительным расположением ключей. Примем порядок расположения ключей по возрастанию, так как в наших таблицах ключи представлены целыми числами (такое предположение не снижает общности решения поставленной задачи).

Как правило, упорядоченные таблицы делают статическими, поскольку для динамических упорядоченных таблиц при включении и удалении элементов приходится выполнять реорганизацию таблиц сразу при выполнении операций, что увеличивает время выполнения этих операций. Тем не менее, возможны и динамические таблицы.

Обычно упорядоченные таблицы отображаются вектором, и это позволяет существенно ускорить поиск по сравнению с перемешанными таблицами.

1. Упорядоченная таблица-вектор

В упорядоченной таблице-векторе элементы располагаются по возрастанию значений ключей, что позволяет делать некоторые предположения о месте размещения искомого элемента таблицы. Если, например, нам требуется найти элемент с ключом k^*, и нам известно, что в i-ом элементе таблицы ключk_i > k^*, это означает, что искомый элемент может находиться среди первых (i-1)-го элементов таблицы. На этом основан алгоритм двоичного поиска.

В соответствии с алгоритмом двоичного поиска определяется индекс записи, находящейся в середине таблицы. Сравнение искомого ключа и ключа найденного элемента позволяет определить (если они не равны), в какой половине таблицы – верхней или нижней – может находиться искомый элемент. В соответствии с принятым решением ненужная половина таблицы, включая и найденную запись, исключается из рассмотрения, в результате чего количество элементов, которые нужно проанализировать, сокращается вдвое. Таким образом, через некоторое количество попыток запись с требуемым ключом, если она имеется в таблице, будет найдена. Если же требуемая запись отсутствует в таблице, через некоторое количество попыток все элементы таблицы будут исключены из рассмотрения.

Схема алгоритма приведена на рис. II–41.

Рис. II–41

Текст функции приводится ниже и в файле tab2vec.cpp.

const int M = 20; /* максимальный размер таблицы */

struct Item{

int key;

Type info;

};

Item bintable[M];

/* Поиск элемента в таблице; результат – индекс найденного элемента или –1 */

int binsearch(int nkey)

{

int i = 0, k = M - 1;

while(i <= k){

int j = (i + k) / 2;

if(bintable[j].key == nkey)

return j; /* элемент найден */

if(bintable[j].key < nkey)

i = j + 1;

else

k = j - 1;

}

return -1; /* элемента в таблице нет */

}

Пусть упорядоченная таблица состоит из M = 8 элементов (рис. II–42).

Рассмотрим схему двоичного поиска для разных значений ключей.

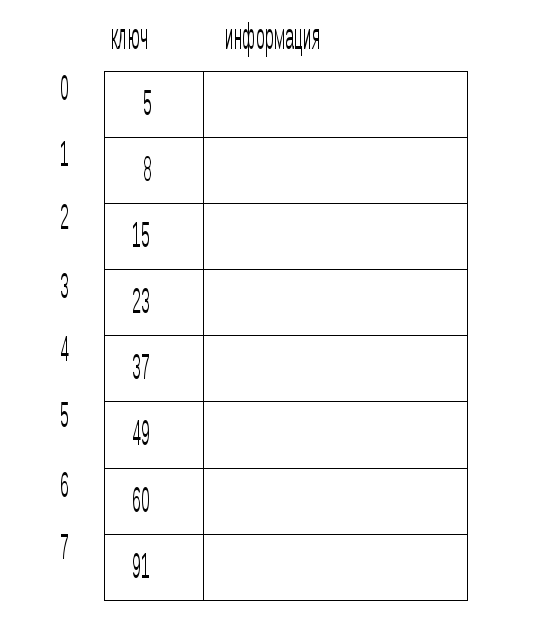
Рис. II–42

(a) Искомый ключ k^*₁= 60

	этап	1	2	3
начало таблицы:	i =	0	4	6
конец таблицы:	k =	7	7	7
середина таблицы:	j =	3	5	6
элемент таблицы:	kj=	23	49	60
возможное место расположения искомого элемента		нижняя половина таблицы	нижняя половина таблицы	искомый элемент найден

(b) Искомый ключ k^*₂= 17

	этап	1	2	3	4	4
начало таблицы:	i =	0	0	1	2	3
конец таблицы:	k =	7	2	2	2	2
середина таблицы:	j =	3	1	1	2	?
элемент таблицы:	kj=	23	8	8	15	15
возможное место расположения искомого элемента		верхняя половина таблицы	нижняя половина таблицы	нижняя половина таблицы	все просмотрено	искомый элемент не найден

В случае таблицы, включающей M элементов, максимальная длина поиска

T= log₂M.

Средняя длина поиска не будет много меньше максимальной.