Очередь-список
При отображении очереди списком можно использовать и линейный, и циклический односвязные списки.
Очередь, отображаемая линейным односвязным списком, задается двумя указателями: на начало очереди (первый элемент списка) и конец очереди (последний элемент списка). В исходном состоянии очередь пуста и оба указателя имеют пустые (NULL) значения (рис.II–28).
Рис. II–28
При записи в очередь первого элемента изменяются оба указателя, так как первый элемент в данной ситуации становится и последним элементом очереди. Последующие операции записи приводят к изменению только указателя на конец очереди (рис. II–28).
При чтении из очереди изменяется указатель на начало очереди. Когда будет прочитан последний элемент, очередь будет пустой и оба указателя (на начало и на конец очереди) должны иметь пустое значение (рис. II–29).
Рис. II–29
При отображении очереди циклическим односвязным списком достаточно иметь один указатель – на последний элемент очереди (last). Первый элемент очереди (циклического списка) будет определяться ее последним элементом; это означает, что указателем на начало очереди будет являться полеnextпоследнего элемента списка, т.е.last->next.
В исходном состоянии очередь пуста, и указатель на конец очереди имеет пустое значение.
При записи в очередь нового элемента будет изменяться указатель на конец очереди – он будет указывать на записываемый элемент. Так как последний элемент очереди служит указателем на начало очереди, в поле nextзаписываемого элемента должно быть записано значение указателя на начало очереди. При записи элемента в пустую очередь, записываемый элемент является и первым, и последним, поэтому данный элемент будет указывать на себя (рис.II–30).
Рис. II–30
При чтении элемента из очереди удаляется первый элемент, поэтому в последнем элементе очереди, на который указывает last, будет меняться значение поля указателя. Когда из очереди будет прочитан последний элемент (перед выполнением операции чтения в очереди находится только один элемент, который является и первым, и последним), указатель на конец очереди должен получить пустое значение (рис.II–31).
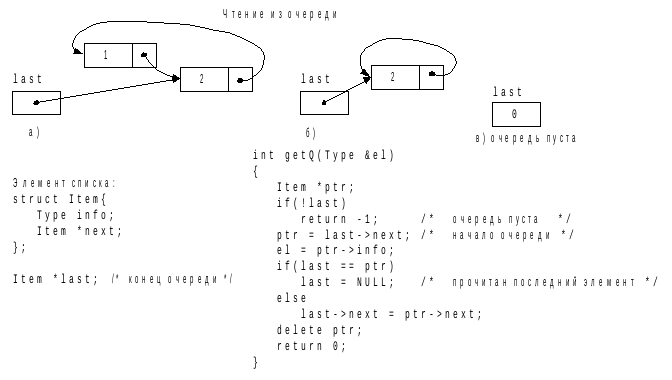
Рис. II–31
Деревья
В данном курсе мы ограничимся рассмотрением бинарных деревьев.
В соответствии с данным выше определением дерева бинарное дерево можно определить как конечное множество узлов, которое либо пусто, либо состоит из корня и двух поддеревьев – левого и правого, каждое из которых является бинарным деревом. Бинарное дерево является упорядоченным, так как для него имеет значение относительный порядок поддеревьев.
Деревья наиболее естественно отображаются в памяти ЭВМ сетями. При отображении двоичного дерева каждый элемент сети, помимо информации, содержит два указателя – на левое и правое поддеревья. Элемент бинарного дерева может быть представлен следующей структурой:
struct Node{
Type info; /* информация, располагаемая в узле дерева */
Node *left; /* указатель на левое поддерево */
Node *right; /* указатель на правое поддерево */
};
Само дерево задается указателем на корень:
Node *proot;
Если дерево пусто, то указатель на корень дерева имеет пустое (NULL) значение. Пустьptrопределяет указатель на некоторый узел дерева (если дерево не пусто, такой узел обязательно найдется). Тогдаptr->leftопределяет левое поддерево данного узла, аptr->right– правое поддерево. Если левое и/или правое поддерево пусты, соответствующее поле (ptr->leftи/илиptr->right) будет иметь пустое значение.
Для работы с древовидными структурами имеется множество алгоритмов, и во всех этих алгоритмах неизменно встречается одна и та же идея – прохождение,илиобходдерева:
Обход дерева – это способ методичного исследования узлов дерева, при котором каждый узел проходится (исследуется) точно один раз.
Полный обход дерева дает линейную расстановку узлов дерева.
Для обхода дерева можно воспользоваться тремя алгоритмами: можно проходить узлы в прямом(прямой обход),обратном(обратный обход) иконцевом(концевой обход) порядках. Эти три обхода определяются рекурсивно. Если бинарное дерево пусто, оно проходится без выполнения каких-либо действий; в противном случае прохождение выполняется в три этапа:
Прямой обход дерева (КЛП):
попасть в корень (К),
пройти левое поддерево (Л),
пройти правое поддерево (П).
Обратный обход дерева (ЛКП):
пройти левое поддерево (Л),
попасть в корень (К),
пройти правое поддерево (П).
Концевой обход дерева (ЛПК):
пройти левое поддерево (Л),
пройти правое поддерево (П),
попасть в корень (К).
Примеры обходов дерева приведены на рис. II–32.
Рис. II–32
В силу рекурсивности структуры двоичного дерева реализация алгоритмов обхода дерева оказывается очень простой, если система программирования допускает создание рекурсивных функций. Так как язык С/С++ обладает такими возможностями, функции обхода дерева, написанные на С/С++, выглядят следующим образом:
struct Node{
char *info; /* информация, располагаемая в узле дерева */
Node *left; /* указатель на левое поддерево */
Node *right; /* указатель на правое поддерево */
};
int cnt; /* порядковый номер узла дерева в процессе обхода */
/* прямой обход дерева */
void straight(Node *root)
{
/* если дерево пусто, не выполнять никаких действий – обход дерева завершается */
if(!root)
return;
/* здесь выполняется необходимая обработка корня – например,
вывод информации в выходной поток */
printf("%d. \"%s\"\n", ++cnt, root->info);
/*обход левого поддерева */
straight(root->left);
/*обход правого поддерева */
straight(root->right);
}
/* обратный обход дерева */
void reverse(Node *root)
{
/* если дерево пусто, не выполнять никаких действий – обход дерева завершается */
if(!root)
return;
/*обход левого поддерева */
reverse(root->left);
/* здесь выполняется необходимая обработка корня – например,
вывод информации в выходной поток */
printf("%d. \"%s\"\n", ++cnt, root->info);
/*обход правого поддерева */
reverse(root->right);
}
/* концевой обход дерева */
void tail(Node *root)
{
/* если дерево пусто, не выполнять никаких действий – обход дерева завершается */
if(!root)
return;
/*обход левого поддерева */
tail(root->left);
/*обход правого поддерева */
tail(root->right);
/* здесь выполняется необходимая обработка корня – например,
вывод информации в выходной поток */
printf("%d. \"%s\"\n", ++cnt, root->info);
}
Тексты функций приведены также в файле tree.cpp.