Міністерство освіти і науки України

Головне управління освіти і науки Дніпропетровської облдержадміністрації

Дніпропетровське відділення МАН України

Відділення: Комп’ютерних наук

Секція:

Задача комівояжера

Роботу виконав:

учень 11-го класу

Дніпропетровського ліцею

інформаційних технологій

при Дніпропетровському національному

університеті імені Олеся Гончара

Наукові керівники:

Дніпропетровськ-2011

ЗМІСТ

Дніпропетровськ-2011 1

Вступ 3

1. Теоретична частина 5

1.1. Теоретична частина з математики 5

1.2. Теоретична частина з інформатики 18

2. Опис роботи 21

3. Структурна схема 28

4. Посібник користувача 29

5. Фрагменти програмного коду 36

5.1. Метод повного перебору 36

5.2. Метод гілок та меж 37

5.3. Жадібний алгоритм 43

6. Апаратні вимоги 44

7. Комплектація програми 44

8. Напрямки використання 44

Висновки 45

Додатки 45

Вступ

Тема даної роботи може викликати іронічну посмішку. Невже знайдуться такі чудаки, які цікавляться діяльністю та турботами комівояжерів, які майже зникли з лиця землі? Треба прямо сказати, що таких людей, принаймні серед математиків, не має. Але до цієї задачі, яка має свою двохсотлітню історію, цікавість математиків не тільки не слабшає, а навіть постійно зростає.

Актуальність теми полягає у тому, що кожна людина завжди шукає оптимальний шлях вирішення своїх проблем і не тільки. Більшість людей зустрічаються з проблемою вибору оптимального, найдешевшого, найкоротшого шляху. Наприклад, якщо ви захотіли поїхати відпочити за кордон та відвідати багато цікавих місць, ви обов’язково складаєте маршрут відвідувань. І при його складанні перед вами постає проблема вибору такого шляху, який би був не дуже довгий, щоб не втомитися в дорозі та, який би був не дуже дорогий. Можна навести приклади великої кількості проблем, які зводяться до розв’язання задач оптимізації, до яких відноситься історично відома задача комівояжера.

У 1859 р. У. Гамільтон придумав гру "Навколосвітня подорож", що складається у відшуканні такого шляху, щоб він проходив через усі вершини (міста, пункти призначення) графа, і щоб можна було відвідати кожну вершину одноразово і повернутися в початкову. Спочатку задача виникла як розважальна гра, але згодом вона втратила цей характер й знайшла безліч практичних застосувань. Перші згадки в якості математичної задачі на оптимізацію належать Карлу Менґеру, який сформулював її в математичному колоквіумі в 1930 році наступним чином: «Ми називаємо проблемою женця (оскільки це питання виникає в кожного листоноші, зокрема, її вирішують багато мандрівників) завдання віднайти найкоротший шлях між скінченною множиною місць, відстань між якими відома». На сьогоднішній день вже запропоновано велику кількість алгоритмів для вирішення задачі комівояжера. Найбільш цікаві (з точки зору автора роботи) з них будуть розглянуті в ній.

Метою даної роботи є створення програми, яка представляє розгляд, опис та порівняння методів розв’язку задачі комівояжера, бо знаходження оптимального методу її розв’язку й на сьогоднішній день дуже актуально, та показати на наглядному прикладі, де може застосовуватися ця задача.

Отже, у роботі представлені теоретичні відомості про задачу комівояжера, розділ за допомогою якого програма розв’язує задачу комівояжера трьома, на думку автора, найбільш основними методами та робить зіставлення цих методів між собою на якісність, на базі виданих при вирішенні програмою результатів, а також присутній розділ, який на наглядному прикладі показує користувачеві один з найпоширеніших прикладів її застосування.

1.Теоретична частина

1.1.Теоретична частина з математики

Математична модель будь якої практичної задачі типу задачі комівояжера (ЗК)

Практичні задачі типу ЗК можуть бути представлені з будь-якої галузі, сфери та науки. Математична модель будь-якої практичної задачі типу ЗК є такою:

Дано деяку кількість N пунктів, попарна відстань між якими нам відома. Потрібно вийти з першого пункту і пройти усі інші (N-1) пунктів, за умовою того, що кожен пункт треба пройти лише один раз і повернутись до першого. Вимагається знайти такий маршрут руху, при якому сумарна пройдена відстань буде мінімальною.

До створеної математичної моделі можуть бути зведені не тільки задачі на знаходження мінімальної суми відстаней між пунктами, а й інші задачі, в яких:

• під пунктами має розуміють об’єкти з будь-якої галузі, сфера науки, наприклад: міста, стан верстата, обладнання після різних операцій, стан економічної одиниці тощо;

• під відстанями вважають вартість проїзду, витрати пального на дорогу тощо.

Приклад Задачі комівояжера та зведення її до математичної моделі

Задача про станок

Практична модель

Деталь в процесі обробки на станку виконує декілька операцій. При переході від однієї операції до іншої станку треба заново налаштовуватися, що приводить до втрати часу. Потрібно знайти такий порядок проведення усіх операцій (з поверненням станку до початкового стану), при якому сумарні втрати часу при переході були б мінімальними, якщо час на перехід операцій відомий.

Математична модель

Дано k операцій, які виконує станок в процесі обробки деталі. Станку треба почати обробку з вихідної точки, зробивши інші (k-1) операцій по одному разу і повернутися до вихідної точки. Треба знайти найменший сумарний час за усі переходи між операціями, послідовність виконання цих операцій не є важливою.

Введення матриці

Матриця – математичний об'єкт, записаний у вигляді прямокутної таблиці чисел m x n. Звичайно матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці не прямокутної форми. Але для ЗК потрібна проста, двовимірна матриця.

У кожного елемента a_ij матриці є два нижні індекси: перший «i» вказує на номер рядка, в якому знаходиться елемент, а другий «j» - на номер стовпця. Також можна говорити «матриця розміром m на n», де m – це кількість рядків, і n – кількість стовпчиків. Обов’язковим зауваженням до матриці є 0 < i ≤ m, 0 < j ≤ n.

Отже, введемо матрицю і застосуємо її в ЗК. Матриця класичної ЗК є симетричною, бо відстані з пункту А до Б та з Б до А однакові, тому значення матриці теж однакові : a_ij = a_ji.

Але існують задачі, які приводять до несиметричних матриць. З розглянутих вище задач – це задачі про плавця та задача про налаштування станка. В цих задачах відстані з пункту А до Б і з Б до А не обов’язково однакові, за умовою задачі, тому деякі значення матриці можуть бути не однаковими : a_ij ≠ a_ji.

В задачі про станок несиметрична модель матриці. Дані матриці (a_ij) – час переходу станку між операціями. Введемо матрицю.

Номер операції	I	II	III	IV	V
I		0	11	5	20
II	31		0	52	8
III	9	16		0	41
IV	64	31	61		0
V	0	93	19	7

Введення графа. Гамільтонов граф. Гамільтонов цикл

Для подальшого розглядання методів рішення ЗК потрібно розглянути елементи теорії графів.

Теорія графів – це розділ математики, особливістю якої є геометричний підхід до вивчення об'єктів. Теорія графів перебуває зараз у самому розквіті. Зазвичай її відносять до топології (тому що в багатьох випадках розглядаються лише топологічні властивості графів), однак вона перетинається з багатьма розділами теорії множин, комбінаторної математики, алгебри, геометрії, теорії матриць, теорії ігор, математичної логіки і багатьох інших математичних дисциплін. Основний об'єкт теорії графів – граф і його властивості та види.

Г

рис.1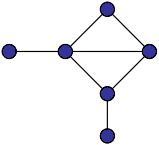

раф (рис.1) – це сукупність точок на площині та ліній, що поєднують деякі з них (можливо й всі точки). Точки представляються як вершини, або вузли графа, а лінії – як дуги, або ребра. Позначати вершини, вузли графа можна або великими латинськими літерами, або числами, або якось інакше(в залежності від умови). Ребра, дуги будемо позначати парою вершин(вузлів) – кінців цього ребра, наприклад: АВ, (i,j), 1-2, 7-12, Київ-Дніпропетровськ і т.д. Також ребра можна позначати маленькими латинськими літерами: a₁, a₂, a₃, …,a_n і т.д. Також сам граф позначають G(V,E), де V – це множина вершин (вузлів), а E – множина ребер.

З означення випливає, що ребро не обов’язково повинно бути прямою лінією. Воно може бути будь-якої форми (дуга, стрілка тощо).

Маршрутом в графі називається послідовність ребер графа, для якої початок кожного наступного ребра співпадає з кінцем попереднього.

Шляхом від A до B в графі називається така послідовність ребер, що веде з A к B, в якій кожні два сусідні ребра мають спільну вершину і ніяке ребро не зустрічається більш ніж один раз.

Циклом називається шлях, в якому співпадають його кінцева та початкова вершини.

Довжиною шляху називається число ребер цього шляху.

Д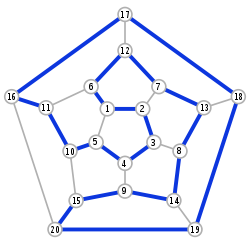 овжиною циклу – число ребер в цьому циклі.

Гамільтонов граф (рис.2) – в теорії графів це граф, що містить Гамільтонов ланцюг або Гамільтонов цикл.

Г

рис.2

амільтонов шлях (або Гамільтонов ланцюг) – шлях (ланцюг), що містить кожну вершину графа рівно один раз. Гамільтонов шлях, початкова і кінцева вершини якого збігаються, називається Гамільтоновим циклом.

Також для несиметричної ЗК потрібно розглянути Орієнтований граф (рис.3) – граф, ребрам якого присвоєно напрямок. Спрямовані ребра іменуються також дугами або орієнтовними ребрами.

Г

рис.3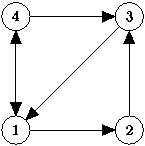

амільтонов шлях, цикл і граф названі на честь ірландського математика У. Гамільтона, який вперше визначив ці класи, дослідивши завдання «кругосвітньої подорожі». Додекаедр, вузлові вершини якого символізували найбільші міста Землі, а ребра – їх з’єднання дорогами.

В термінах теорії графів симетричну ЗК можна сформулювати так:

Дана повна мережа з n вершинами, довжина ребра (i,j)= a_ij. Знайти гамильтонов цикл мінімальної довжини.

Для несиметричної задачі формулювання зміниться, за рахунок умови:

Дана повна мережа з n вершинами, довжина дуги чи стрілки (i,j) = a_ij. Потрібно знайти гамільтоновий цикл мінімальної довжини.

Деякі прикладні задачі формулюються як ЗК, але в них потрібно мінімізувати довжину не гамильтонового циклу, а гамильтоновий ланцюги. Такі задачі називаються незамкнутими. Деякі моделі зводяться до задачі про декількох комівояжерів, але ми тут їх розглядати не будемо.