===================================================

Т.9. Термогазодинамический расчет и зависимость удельных параметров ТРД, ТРДФ и газогенераторов ГТД от параметров рабочего процесса.

ТРД может быть иметь различные исполнения: одновальный ТРД с нерегулируемым компрессором (_к6); для расширения диапазона режимов работы ТРД с регулируемыми ступенями (_к=6 – 8); двухвальный ТРД. При большом диапазоне чисел Маха применяют регулирование сопла (критическое и выходное сечения).

Рис.9.1. Одновальный ТРД с нерегулируемым компрессором.

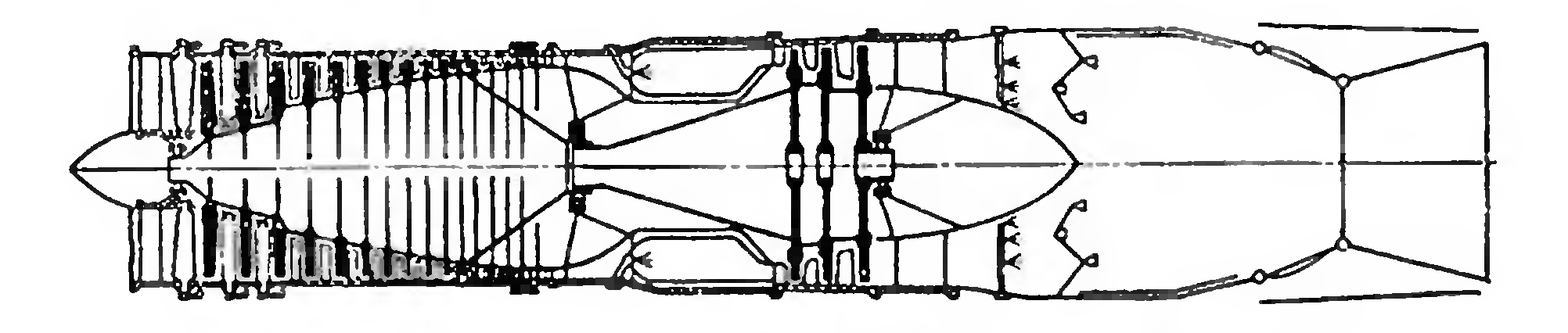
Рис.9.2. Одновальный ТРДФ с регулируемым компрессором и соплом.

Рис.9.3. Двухвальный ТРДФ с регулируемым соплом.

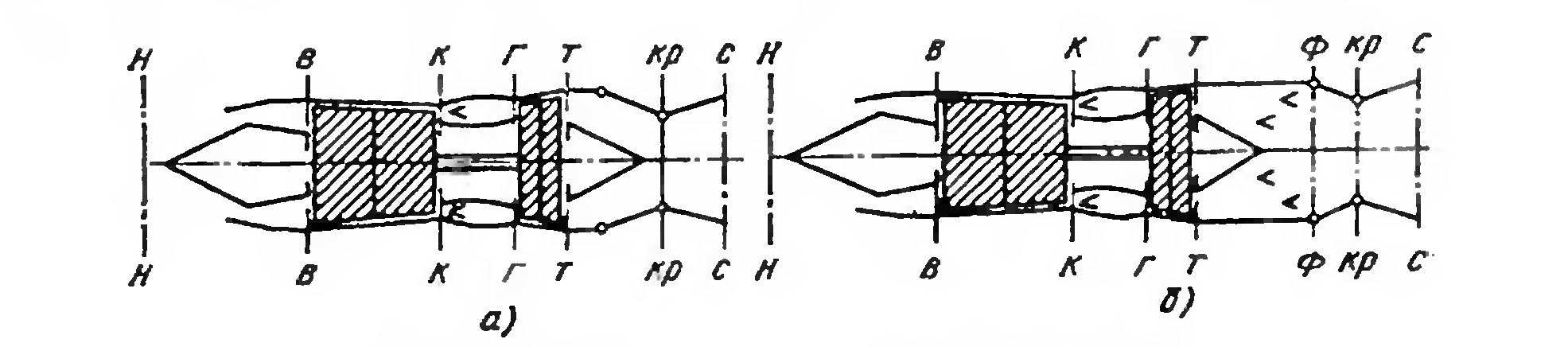
Рис.9.4. Расчетные схемы а – ТРД, б – ТРДФ.

Двухконтурные и турбовальные (со свободной турбиной) ГТД. Как ТРД и ТРДФ, ТРДД и ТВлД имеют в своем составе один общий агрегат – газогенератор.

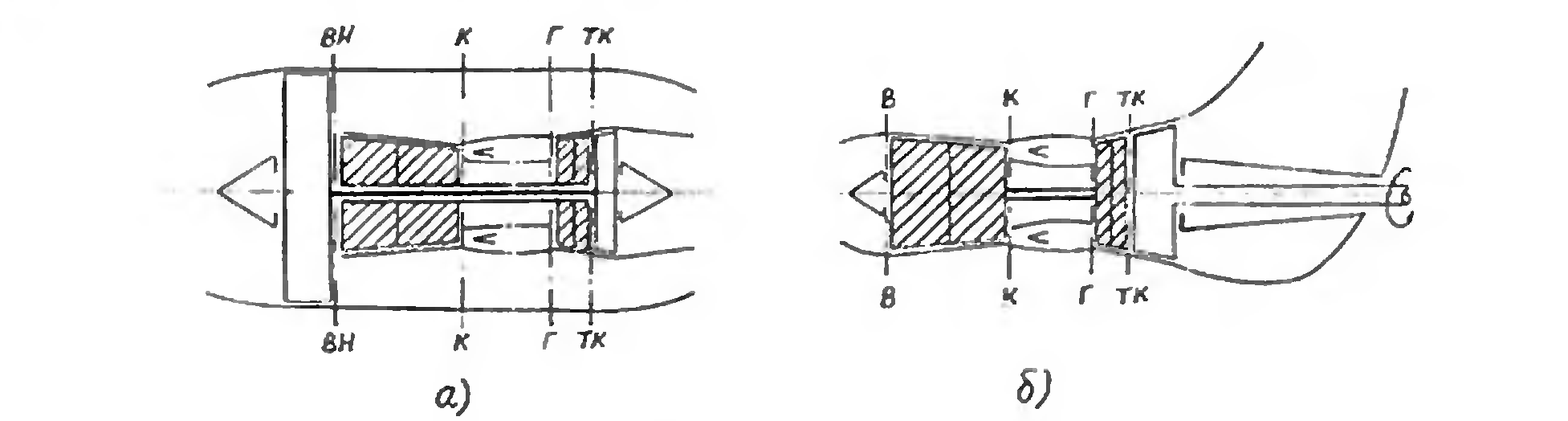
Рис.9.5. Расчетные схемы а – ТРДД, б – ТВлД.

9.1. Термогазодинамический расчет трд, трдф и газогенераторов гтд на расчетном режиме.

Математическая модель.

0, I, II и IV уровни математических моделей ГТД.

Цель расчета: определение удельных параметров P_уд, С_уд и расхода воздуха G, а также проходных сечений F_i.

Математическая модель I уровня. Базируется на уравнениях балансов:

- баланс мощностей в роторах;

- баланс расходов в контурах;

N_T=N_K, n_т=n_к (9.1)

N_твд=N_квд, n_твд=n_квд (9.2)

N_тнд=N_кнд, n_тнд=n_кнд (9.3)

Баланс расходов

Расход воздуха через камеру сгорания:

G_вкс = G_в(1 – _отб) (9.4)

Расход газа через турбину

G_г = G_вкс(1+q_т)=G_в(1 – _отб) (1+q_т) (9.5)

Расход газа через форсажную камеру или реактивное сопло

G_гт = G_г + G_в_воз=G_в[(1 – _отб) (1+q_т)+_воз] (9.6)

Расход газа через реактивное сопло

G_гс = G_гт + G_вq_тф =G_в[(1 – _отб) (1+q_т)+_воз+q_тф] (9.7)

i_к=i_в+i_в (9.8)

i_кc=i_к+i_кс (9.9)

i_Т=i_ксi_т (9.10)

p^*_к= p^*_в^*_к

Давление за камерой сгорания

p^*_кс= p^*_к_кс

Давление за турбиной

p^*_т= p^*_кс/^*_т

Давление за реактивным соплом

p^*_с= p^*_т_г

При проведении расчета по математической модели I уровня заданы М, Н, Р. Выбирают

^*_к, Т^*_г;

На основе опыта проектирования принимают значения коэффициентов, характеризующих совершенство узлов

Для определения проходных сечений F_i задают также скорости в этих сечениях _i.

Расчет ведется последовательно, по сечениям от входа к выходу. По заданной высоте по стандартной атмосфере (ГОСТ 4401-81) определяют давление, температуру и скорость звука. По заданному М выбирают тип ВУ, выбирают _вх.

Определяют давление и температуру на входе в компрессор

Температуру и давление за компрессором

p_к=p^*_в^*_к

Параметры газа перед турбиной

p_кс=p^*_к_кc

относительный расход воздуха

q=1/L₀

Из условий баланса расходов и баланса мощностей определяют ^*_т и находят давление и температуру за турбиной

p^*_т=p^*_кс/^*_т

Определяют параметры потока перед реактивным соплом

p^*_с=p^*_т_г

Перепад на сопле

^*_с= p^*_с/р_н

Скорость истечения из сопла

Определяют удельные параметры двиателя

Р_уд=с_с – V_п,

С_уд=3600q_т/Р_уд

Расчет проходных сечений производят по уравнению расхода

Определяя расходы по уравнениям баланса расходов, из уравнения расхода определяют площади проходных сечений

На этом расчет завершается.

9.2. Зависимости удельной тяги и удельного расхода топлива трд от параметров рабочего процесса.

III – IV поколений.

Рис. 9.6. Изменение Р_уд и С_уд в зависимости от ^*_к (а) и Т^*_г (б) при Н=0.

Н=0, М=0; Т^*_г =1600 К (а), ^*_к = 15 (б).

С ростом ^*_к Р_уд сначала растет, достигает максимума при ^*_к < 20, затем снижается. Это связано с работой цикла, которая имеет максимум по ^*_к. Удельный расход топлива изменяется по ^*_к с минимумом, который достигается при очень больших ^*_к.

С ростом температуры Р_уд монотонно растет, а С_уд имеет максимум при крайне низких температурах.

Удельная тяга зависит от эффективной работы цикла

Р_уд=с_с – V_п

При постоянной скорости полета удельная тяга однозначно определяется эффективной работой цикла.

Рассмотрим зависимости Р_уд и С_уд, а также L_e, Q и к.п.д. – эффективного, полетного и общего от ^*_к и Т^*_г.

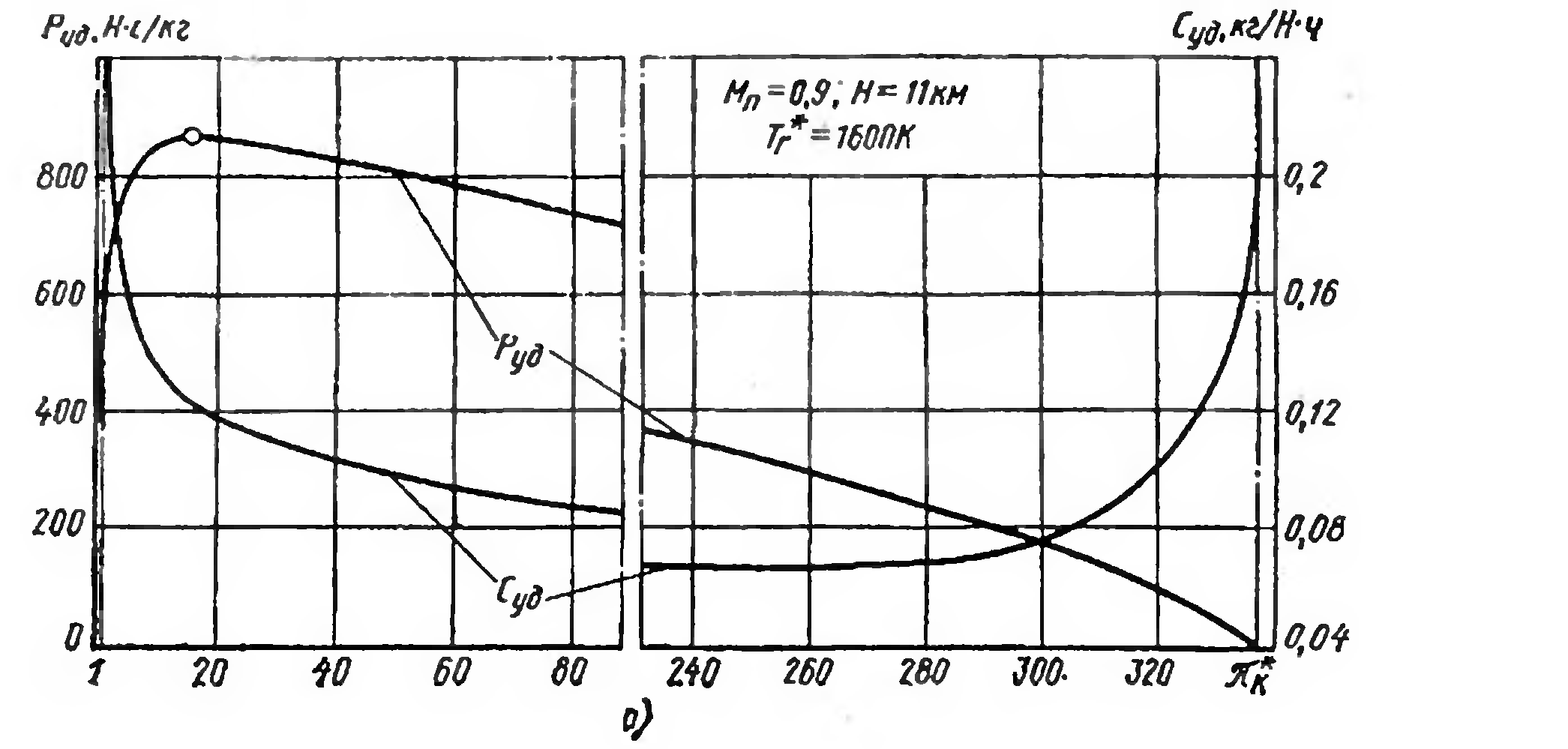
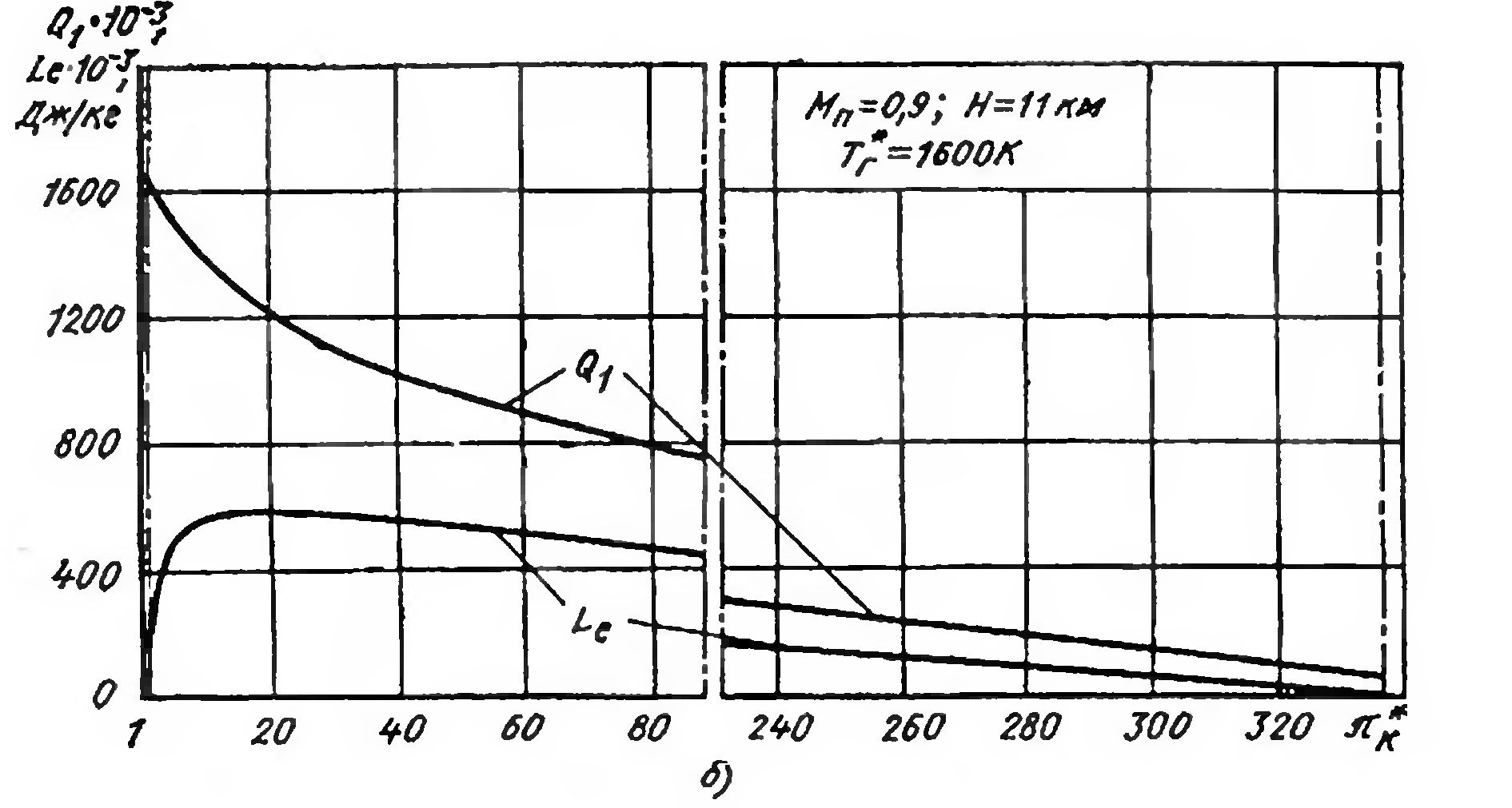
Рис.9.7. Зависимости Р_уд и С_уд (а), L_e и Q (б), _t, _е, _п, _о (в) от ^*_к; Т^*_г=1600 К; М=0,9, Н=11 000.

Удельная тяга изменяется по ^*_к с максимумом, а удельный расход топлива – с минимумом. Изменение удельной тяги повторяет изменение эффективной работы цикла, которая, при малых ^*_к возрастает, поскольку более полно используется тепло подведенное в цикле (относительно меньше тепла отводится в цикле). При больших ^*_к падение эффективной работы вызвано ростом относительных затрат на преодолении потерь при сжатии и расширении. Подведенное в цикле тепло с ростом ^*_к падает.

Поведение удельного расхода топлива удобнее пояснить, используя зависимости к.п.д. от ^*_к, т.к.

С ростом ^*_к термический к.п.д. монотонно растет (не учитываются потери), а эффективный к.п.д. _е=L_e/Q₁ изменяется с максимумом по тем же причинам, что и эффективная работа, т.к. подведенное к циклу тепло монотонно уменьшается. Полетный к.п.д. растет с увеличением ^*_к, а общий к.п.д. изменяется с максимумом, расположенном в области нерабочих значений ^*_к. Удельный расход топлива имеет минимум при тех же значениях ^*_к.

Зависимости Р_уд, С_уд, L_e, Q, _t, _е, _п, _о от Т^*_г представлены на рис.9.8. Удельная тяга с ростом температуры монотонно растет (растет скорость истечения), а удельный расход топлива имеет минимум по Т^*_г, расположенный в области очень низких температур. Существование и положение минимума обусловлены максимумом _о по Т^*_г. Этот максимум является компромиссом между зависимостями от Т^*_г полетного и эффективного к.п.д. Эффективный к.п.д. растет с ростом Т^*_г, а полетный падает.

Рис. 9.8. Зависимости Р_уд и С_уд (а), L_e и Q (б), _t, _е, _п, _о (в) от Т^*_г; ^*_к=15; М=0,9, Н=11 000.

Найдем оптимальное значение ^*_к, соответствующее максимуму Р_уд. Для этого продифференцируем по ^*_к выражение для Р_уд

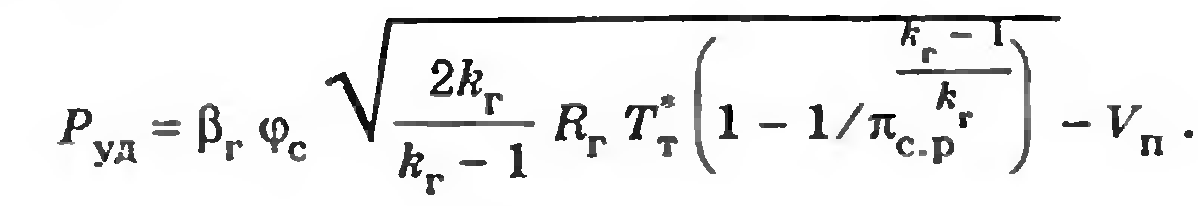
где, _г  коэффициент изменения массы – параметр, учитывающий влияние отбора и возврата воздуха, подвода топлива в основной и форсажной камерах. Расчетное отношение давлений на сопле заменим по формуле

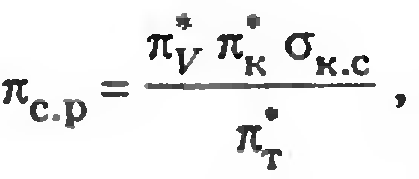
Тогда в результате дифференцирования получим

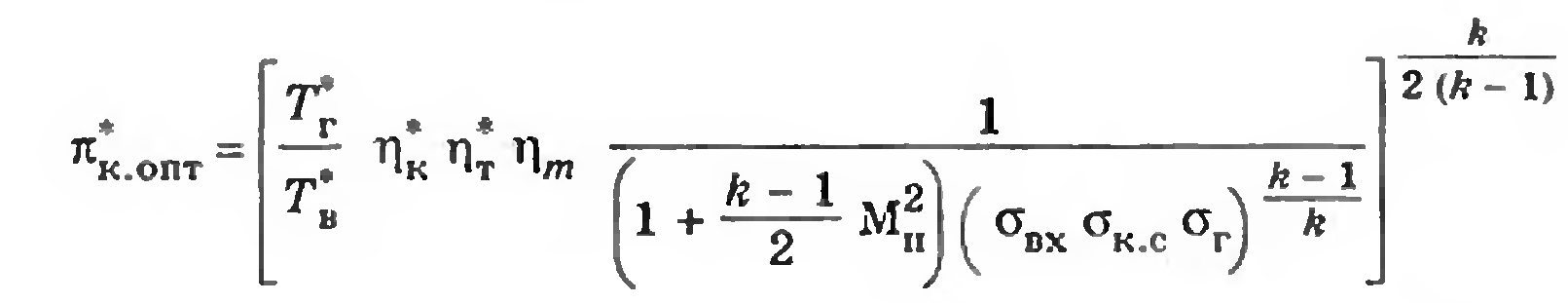
Оптимальное значение ^*_к растет с ростом степени подогрева, с увеличением потерь во входном устройстве, камере сгорания и в затурбинном объеме, и снижается с ростом числа Маха и ростом механических потерь и потерь на сжатие и расширение.

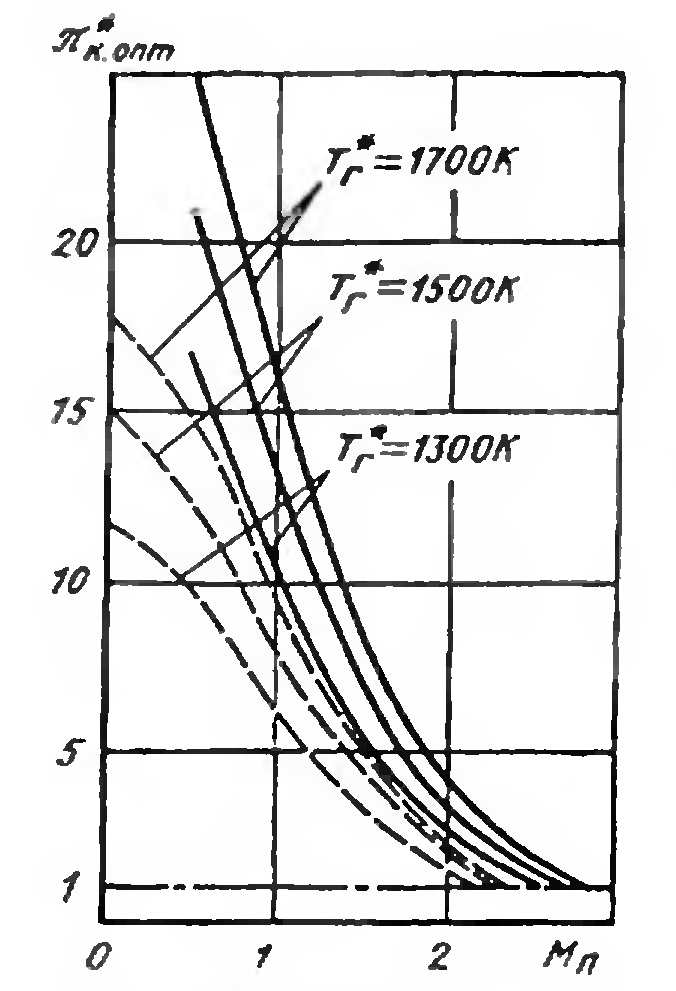
Рис.9.9. Зависимость ^*_к.опт от числа Маха полета;

Сплошные линии Н=11 000, пунктир Н=0.

С ростом М_п ^*_к.опт уменьшается, т.к. растет ^*_в (сжатие в воздухозаборнике). ^*_к.опт растет с увеличением высоты полета, т.к. понижение температуры на входе при постоянной Т^*_г означает рост степени подогрева, а с ростом степени подогрева растет ^*_к.опт.