3. Линейные м-последовательности

Несколько худшие автокорреляционные функции по сравнению с сигна­лами Баркера имеют линейные рекуррентные М-последовательности.

Рекуррентные М-последовательности являются периодическими числовыми последовательностями с периодом N , который определяется по формуле

,

где m – память последовательности.

М-последовательности получаются при определенном наборе коэффициентов С_m , соответствующих структуре неприводимых примитивных полиномов степени m. Рекуррентное правило образования имеет вид

,

где знак означает суммирование по модулю 2. Для формирования М-последовательности задается начальная кодовая комбинация а₁ , а₂ , …, а_m, а в таблице неприводимых примитивных полиномов находятся комбинации С_m для соответствующего полинома.

Для линейной М-последовательности отношение величины главного максимума к максимальному значению бокового лепестка автокорреляционной функции приближенно растет как величина , где п = 2^ - 1 — число импульсов в последовательности;  — целое положительное число.

В определенной степени линейные рекуррентные последовательности об­ладают свойством хаотичности, которое заключается в следующем. Если из периода следования такой последовательности, содержащей п членов, вы­брать возможные отрезки по  членов в каждом, то:

• среди этих отрезков не будет совпадающих;

• среди них найдутся любые комбинации из +1 и -1, состоящие из  членов (кроме запрещенной комбинации, включающей только +1).

Эти свойства сходны со свойствами случайных разнополярных последова­тельностей, поэтому М-последовательности часто называют псевдослучайными, или шумоподобными последовательностями. К тому же автокор­реляционная функция М-последовательности имеет форму, сходную с АКФ квазибелого шума с ограниченным спектром. При передаче псевдослучайных последовательностей по высокочастотному каналу обычно применяется фазо­вая или относительная фазовая модуляция.

4. Функции Радемахера и функции Уолша

Аналитическая интерпретация этих функций встречает определенные сложности, однако идея их построения сравнительно проста. Функции Раде­махера образуются из синусоидальных функций с помощью соотношения

,

где аргумент  = t / T — безразмерное время; Т — период функции; k = 0, 1,2, ... — порядок функции. Символом sign (сигнум - функция) в математике обоз­начается функция

sign (x) = 1, х  ; -1, х  .

Функции Радемахера, принимающие значения ±1, можно трактовать как функции «прямоугольного синуса», и они имеют форму меандра. На рис. 105 показаны временные диаграммы первых четырех функций Радемахера. Нетрудно заметить, что функции Радемахера :

ортонормированны на интервале 0 … 1.

Дальнейшим развитием систем функций типа последовательностей Радемахера, имеющих форму «прямоугольной волны», стала ортонормированная система функций (последовательностей) Уолша (Walsh). Широко используе­мые в технике связи последовательности Уолша — одни из немногих известных в математике с 1922 г. ортонормированных функций, которые на отрезке своего существования (периоде следования -Т/2, Т/2) принимают лишь два значения: +1 или -1.

Введем безразмерное время, нормированное к периоду следования  = t/T, и обозначим k-ю (k — порядок) функцию Уолша принятым в математике символом wal(k : ). Идею построения последовательностей Уолша можно уяснить из рис. 106, где показаны первые восемь этих функций. Ортонормированность данных функций следует из принципа их построения и может быть проверена непосредственно путем вычисления интеграла.

Функции Уолша нормированы к единице при любом порядке k.

Рис. 105. Временные диаграммы первых

четырех функций Радемахера

При перемножении двух функций Уолша получается также функция Уолша (свойство мультипликативности).

Из рис. 106 можно заметить, что четным относительно середины интерва­ла определения ( = 0) функциям Уолша соответствуют четные номера k, а нечетным функциям — нечетные номера. Такое взаимно-однозначное соот­ветствие между четностью функций и четностью их номера k аналогично свойствам гармонических функции

; .

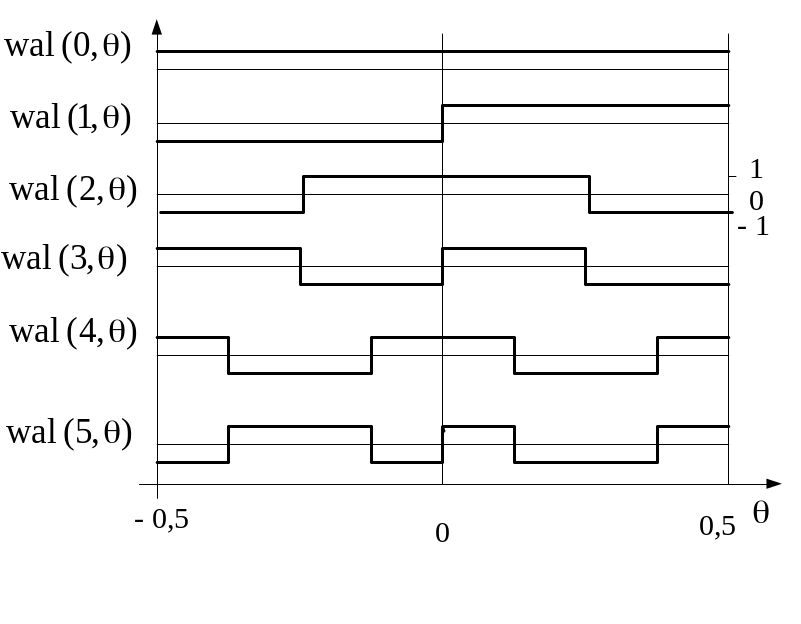
Рис. 106. Восемь первых функций Уолша

Поэтому в ряде случаев используются обозначения cal (k, ) для четных функций и sal (k, ) для нечетных функций Уолша. Эти функции связаны сле­дующими соотношениями:

cal (k,) = wal (2k, ); sal (k, ) = wal (2k : -1, ).

Способ нумерации функций Уолша в системе называется упорядочением. Разработаны и существуют несколько принципов упорядочения функций Уолша. Функции Уолша, показанные на рис. 106, упорядочены по Уолшу. В ряде практических задач удобнее пользоваться другими способами упоря­дочения. Наиболее часто применяются системы функций Уолша, упоря­доченные по Адамару и Пэли.

Заключение. Высокая помехоустойчивость ШПС обеспечивает и высокую скрытность систем связи. Это обусловлено тем, что требуемое время анализа параметров сигнала существенно больше длительности сигнала. Кроме того, прием ШПС требует знания самой М-последовательности, вскрытие которой представляет весьма трудную задачу.

Использование ПШС дает возможность передачи в той же полосе узкополосных сигналов. При приеме ПШС будут выполняться преобразования в исходный узкополосный сигнал. При этом принимаемые узкополосные сигналы преобразуются этими устройством в ШПС и не оказавают влияния на обработку сигнала.

1. В чем отличие спектров немодулированной периодической последовательности видеоимпульсов и АИМ-сигнала? 2. Сформулируйте теорему Котельникова. 3. Поясните сущность преобразований, выполняемых над сигналом при переходе от аналогового представления к цифровому. 4. Поясните сущность трех видов цифровой модуляции: ЦАМ, ЦФМ, ЦЧМ. 5. В чем заключается принцип импульсно-кодовой модуляции? 6. Как осуществляется цифровая частотная модуляция? 7. Как осуществляется цифровая фазовая модуляция? 8. В чем преимущество сигналов с ФМ по отношению к сигналам с ЧМ ? 9. Что называется базой сигнала?

94