Часто для упрощения схем выделения модулирующего сигнала на приемной стороне используют сигнал с частично подавленной несущей, которая получила название пилот - сигнала.

3. Аналитическое описание радиосигналов с угловой модуляцией

При угловой модуляции по закону передаваемого сообщения изменяется текущая (полная) фаза несущего колебания (14) ψ (t) = соs (ω t + φ₀).

Мгновенная частота и текущая фаза колебания связаны соотношениями:

Отсюда следует, что всякая модуляция фазы колебаний означает модуляцию их частоты, и наоборот.

Если в несущем колебании изменяется частота ω, то имеют дело с частотной модуляци­ей (ЧМ), если же изменяется начальная фаза φ₀ , то имеют дело с фазовой модуляцией (ФМ).

Различия между ЧМ и ФМ определяются прежде всего разной зависимостью индексов модуляции от параметров модулирующего напряжения.

При частотной модуляции несущая частота связана с модулирующим сигналом e (t) зависимостью:

ω (t) = ω₀ + k_ч е (t),

где k_ч — размерный коэффициент пропорциональности между частотой и модулирующим напря­жением.

Рассмотрим однотональную ЧМ, когда модулирующим сиг­налом является гармоническое колебание e (t) = E₀ cos Ω t с нулевой начальной фазой. Пусть также начальная фаза несущего колебания равна нулю. Полную фазу ЧМ-сигнала в любой момент времени t определим пу­тем интегрирования мгновенного значения частоты:

где ω_д.ч = k_чЕ₀ – максимальное отклонение частоты от значения ω₀ , или девиация частоты при частотной модуляции. Отношение

m_ч = ω_д.ч /Ω = k_ч Е₀/Ω,

являющееся девиацией частоты несущего колебания, называют индексом ЧМ. С учетом сделанных замечаний ЧМ-сигнал запишется в виде

. (19)

На рис. 94 представлены временные диаграммы несущего коле­бания и модулирующего сигнала с нулевыми начальными фазами, и полу­ченный в результате процесса частотной модуляции ЧМ-сигнал. Нетрудно заметить, что по форме ЧМ-сигнал напоминает сжатые и растянутые меха русской гармошки.

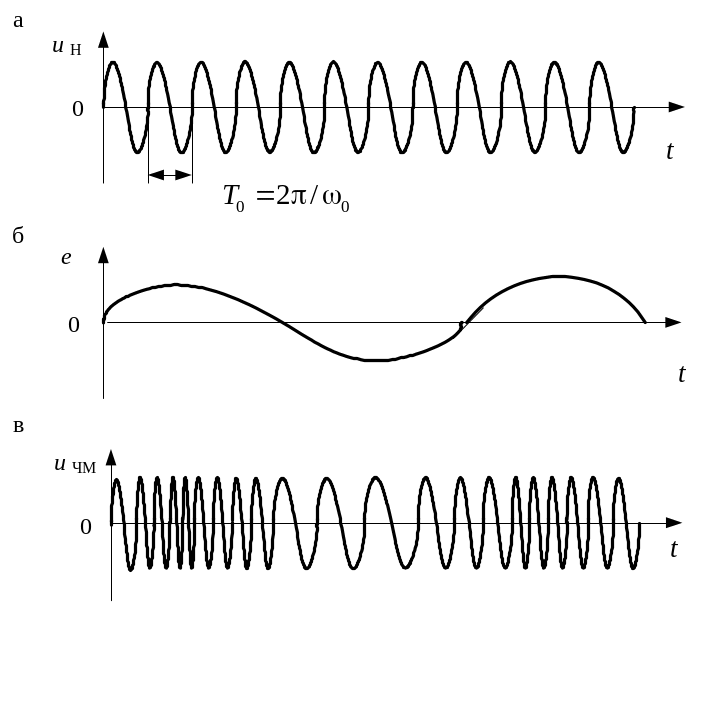
Рис. 94. Частотная однотональная модуляция:

а - несущее колебание; б - модулирующий сигнал; в - ЧМ-сигнал

В ФМ-сигнале полная фаза несущего колебания изме­няется пропорционально модулирующему напряжению и при однотональной модуляции равна

Ψ (t) = ω₀ t + k_ф е (t), Ψ (t) = ω₀ t + k_ф Е₀ cos Ω t,

где k_ф – размерный коэффициент пропорциональности, рад/В.

Отсюда следует, что, как и в случае ЧМ, полная фаза не­сущего колебания при ФМ изменяется по гармоническому зако­ну.

Максимальное отклонение фазы несущего колебания от начальной фазы ха­рактеризует индекс фазовой модуляции

m _ф = k_ф Е_0.

С учетом введенных обозначений запишем ФМ-сигнал:

(20)

Дифференцирование аргумента косинусоиды дает частоту ФМ-сигнала:

ω (t) = ω₀ – m_ф Ω sin Ω t = ω₀ – ω_д.ф sin Ω t

где ω_д.ф = m_ф Ω — максимальное отклонение частоты от значения несу­щей (девиация частоты при фазовой модуляции).

Из сравнения выражений (19), (20) видно, что при однотональной угловой модуляции нельзя определить, является сигнал ЧМ или ФМ. Различия меж­ду этими видами однотональной модуляции проявляются только при изменении амплитуды Е₀ или частоты Ω модулирующего сигнала e (t).

В случае ЧМ девиация частоты (ω_дч = k_чЕ₀) пропорциональна ам­плитуде Е₀ и не зависит от частоты Ω модулирующего сигнала e (t) = Е₀ cos Ω t. Индекс же модуляции т_ч (m_ч = k_ч Е₀/Ω) прямо пропорционален амплитуде Е₀ и обратно про­порционален частоте модулирующего сигнала.

При ФМ девиация частоты ω_д.ф (ω_д.ф = k_ф Е₀ Ω) изменяется пропорционально амплитуде и частоте моду­лирующего сигнала. Индекс модуляции т_ф (k_ф Е₀) пропорционален амплитуде Е₀ и не зависит от частоты модулирующего сигнала.

Сделаем некоторые замечания о спектрах колебаний с угловой модуляцией. Рассмотрим колебание вида

u_мод (t) = U_н cos(ω₀ t + ψ (t)),

в котором передаваемое сообщение зало­жено в функцию фазового угла ψ (t).

При ЧМ функция ψ (t) является интегралом от передавае­мого сообщения.

Ин­тегрирование является линейным преобразованием, поэтому при ЧМ спектр функции ψ (t) будет содержать те же компоненты, что и спектр сообщения e (t), но с изме­ненными амплитудами и фазами.

Если колебание u_мод (t) получено с помощью фазовой модуляции, то ψ (t) и e (t) полностью совпадают по форме и отличаются лишь постоянным коэффици­ентом. При этом очевидно, что с точностью до постоянного коэффициента совпада­ют и спектры функции ψ (t) и e (t).

Определим спектр модулированного колебания u_мод(t), считая заданным спектр функции ψ(t). Для этого воспользуемся тригонометрической формулой представле­ния косинуса суммы двух углов и преобразуем выражение к виду

u_мод(t) = U_н cos ψ(t) cosω₀t – U_н sin ψ(t) sinω₀t = u_c(t) - u_s (t).

Из формулы следует, что в общем случае модулированный по углу сигнал можно рассматривать как сумму двух квадратурных колебаний: косинусного и синусного, каждое из которых модулировано только по амплитуде. Нетрудно также заметить, что закон ам­плитудной модуляции для косинусного колебания определяется «медленной» функцией cos ψ(t), а синусного — «медленной» функцией sin ψ(t).

Но выше указывалось, что для определения спектра АМ-колебания достаточно сдвинуть на частоту ω₀ спектр огибающей амплитуд передаваемого сообщения. Следовательно, для нахождения спектра колебания u_мод(t) сначала необходимо найти спектры функций cos ψ(t) и sin ψ(t), т. е. спектры огибающих квадратур­ных колебаний. Перенос этих спектров на частоту ω₀ можно затем осущест­вить, как и при обычной АМ.

Приведенные рассуждения показывают, что при одном и том же переда­ваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем спектр колебания, модулированного по амплитуде. Действительно, по­скольку cos ψ(t) и sin ψ(t) являются нелинейными функциями по отношению к своему аргументу ψ(t), то их спектры могут существенно отличаться от спек­тра функции ψ(t). При этом возможно возникновение кратных и комбинаци­онных частот, как это имеет место при обычных нелинейных преобразовани­ях спектра.

Данное обстоятельство, а также наличие двух квадратурных слагаемых по­казывает, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты ω₀, как это имеет место при амплитудной модуляции. При угловой модуляции связь между спектрами реального сообщения и модулированного колебания оказывается более сложной.

4. Спектр сигнала при однотональной угловой модуляции

Запишем соотношение для ЧМ-сигнала следующим образом (здесь и далее индекс у коэффициента т опущен):

(12.8)

Проанализируем выражение для малых (т << 1) и боль­ших (т > 1) индексов модуляции.

Спектр ЧМ-сигнала при т << 1. В этом случае имеют место приближенные равенства

С учетом последнего

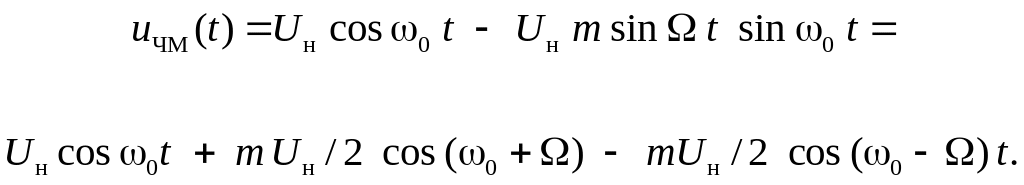
Сравнение соотношений для спектров АМ- и ЧМ-сигналов показывает, что спектр ЧМ-сигнала аналогичен спектру АМ-сигнала и также состоит из несущего коле­бания и двух боковых составляющих с частотами ω₀ + Ω и ω₀ - Ω. Индекс модуляции т играет здесь ту же роль, что и коэффициент амплитудной моду­ляции М. Единственное и принципиальное отличие – знак «минус» перед нижней боковой составляющей в формуле для ЧМ-сигнала, который характе­ризует поворот ее фазы на 180°, что аналитически приводит к превращению АМ-сигнала в ЧМ-сигнал.

На рис. 95а представлена спектральная диаграмма для ЧМ-сигнала при индексе модуляции т << 1. Отметим, что ширина спектра в данном случае равна 2Ω, как и при АМ.

На векторной диаграмме рис. 95б показано, как изменение фазы ниж­ней боковой составляющей на 180° (вектор АD) влияет на вектор результи­рующего колебания ОВ. Направление вектора АD нижней боковой состав­ляющей при АМ-сигнале обозначено штриховой линией. Вектор результирующего коле­бания ОВ изменяется как по фазе, так и по амплитуде, т.е. с течением вре­мени «качается» вокруг центрального положения. Однако при т << 1 изме­нения амплитуды настолько малы, что ими можно пренебречь и модуляцию рассматривать как чисто фазовую.

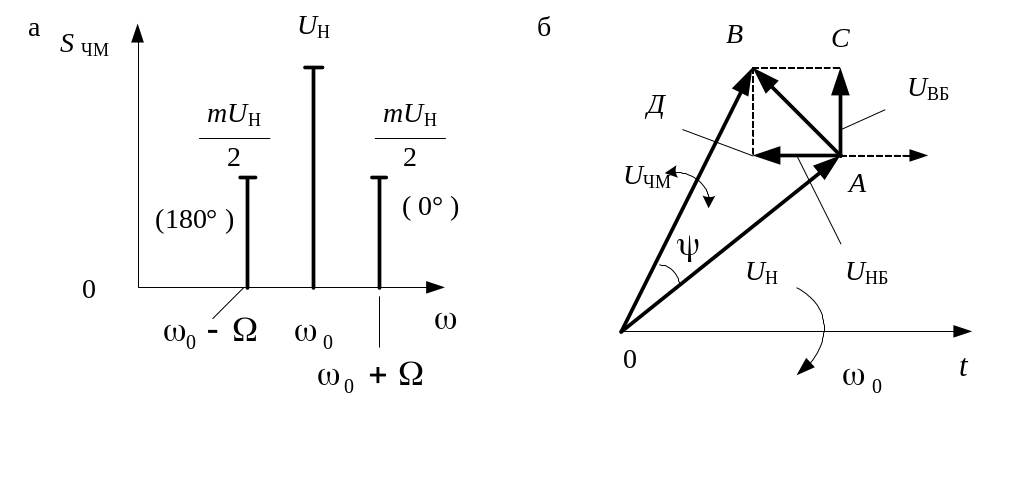
Рис. 95. ЧМ-сигнал:

а - амплитудный спектр; б - векторная диаграмма

Спектр ЧМ-сигнала при т > 1. Здесь при расчетах оказывается удобным представить косинусоиду и синусоиду рядами функций Бесселя. Из математики из­вестно, что эти функции записываются следующим образом:

где J_n(m) – функция Бесселя первого рода n-го порядка, имеющая при отри­цательном порядке значение (рис. 96).

Ряды подставим в формулу (21), а затем заменим произ­ведение косинусов и синусов полусуммами косинусов соответствующих аргу­ментов.

Рис. 96. Графики функций Бесселя

Получим выражение

Итак, спектр ЧМ-сигнала с однотональной модуляцией при индексе модуляции т > 1 состоит из несу­щего колебания и двух групп высоко­частотных гармоник в виде бесконеч­ного числа боковых составляющих с частотами ω₀ + nΩ и ω₀ - nΩ, распо­ложенными попарно и симметрично относительно несущей частоты ω₀. Амплитуды всех составляющих спектра сигнала определяются соответствующими значениями функций Бесселя. Теоретически спектр ЧМ-сигнала (аналогично и ФМ-сигнала) бесконе­чен по полосе частот, однако в реаль­ных случаях он ограничен.

Дело в том, что, начиная с номера порядка п > т + 1, значения функций Бесселя становятся весьма малыми (рис. 96). Поэтому считает­ся, что практическая ширина спектра радиосигналов с угловой модуляцией равна

ЧМ- и ФМ-сигналы, применяемые на практике, как правило имеют индекс модуляции т >> 1, поэтому

Таким образом, полоса частот, занимаемая сигналами с однотональной частот­ной модуляцией, равна удвоенной величине девиации частоты и не зависит от час­тоты модуляции.

Спектр сигналов с угловой модуляцией при негармоническом мо­дулирующем сигнале определить достаточно трудно. Но он всегда сложнее, чем спектр АМ-сигнала при том же модулирующем сигнале. Ширина его спектра так­же значительно больше, чем при амплитудной модуляции.

Примерная структура спектра ЧМ-сигнала при индексе модуляции т = 3 показана на рис. 97.

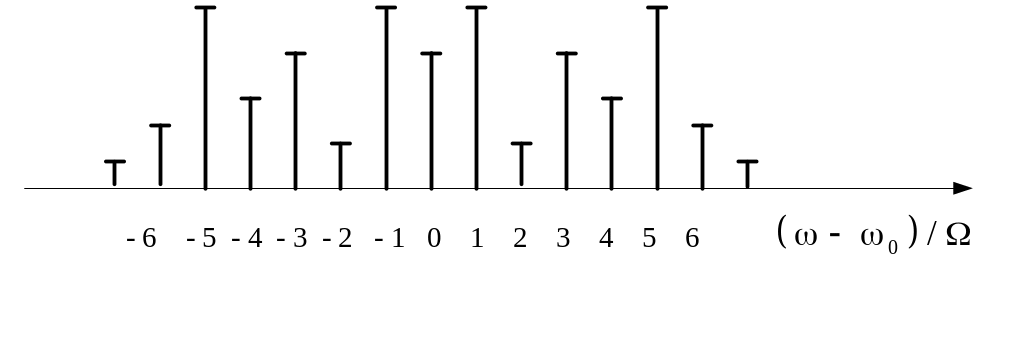
Рис. 97. Спектр ЧМ-сигнала при m = 3

Следует отметить, что радиосигналы с частотной и фазовой модуляцией имеют важные преимущества перед амплитудно-модулированными колебаниями:

1. Поскольку при угловой модуляции амплитуда модулированных колебаний не несет в себе никакой информации и не требуется ее постоянства (в отличие от ам­плитудной модуляции), то практически любые вредные нелинейные изменения ам­плитуды радиосигнала в процессе осуществления связи не приводят к искажению передаваемого сообщения.

2. Постоянство амплитуды радиосигнала при угловой модуляции позволяет полностью использовать энергетические возможности генератора несущей частоты, который работает в этом случае при неизменной колебательной мощности.

Все сказанное справедливо лишь при следующем условии: амплитуда полезного сигнала на входе частотного детектора должна значительно превышать эффектив­ное напряжение шума. В противном случае неизбежен так называемый пороговый эффект. Может оказаться, что ЧМ-система при малом отношении сигнал/шум на входе будет функционировать хуже, чем аналогичная система с АМ-сигналами. Кроме того, для реализации отмеченных преимуществ ЧМ- и ФМ-колебаний необ­ходимо отводить конкретному радиосигналу слишком широкую полосу частот, зна­чительно превышающую ширину спектра модулирующей функции.

5. Особенности ЧМ и ФМ сигналов

При ФМ индекс модуляции m_ф = k_ф Е₀ пропорционален только амплитуде модулирующего напряжения и не зависит от его частоты. Если амплитуда модулирующего сигнала постоянна, а модулирующая частота изменяется, то число боковых частот п и их амплитуды остаются относительно неизменными, изменится их положение в спектре сигнала относительно несущей частоты (спектр при увеличении частоты модулирующего сигнала расширяется, а при уменьшении - сжимается). Полоса частот, занимаемая спектром зависит от индекса модуляции m _ф:

При m_ф << 1 , то есть ширина полосы занимаемых частот такая же, как и при АМ. В этой связи при m_ф<<1 фазовую модуляцию называют узкополосной.

При ЧМ индекс частотной модуляции зависит от частоты модулирующего сигнала m_ч = ω_д.ч /Ω = k_ч Е₀ /Ω. Отсюда следует, что при изменении частоты модулирующего сигнала будут изменяться амплитуды всех составляющих спектра, изменится их положение и количество. Однако если учитывать только те составляющие спектра, амплитуды которых больше 15 % амплитуды несущего колебания без модуляции, то можно показать, что . Следует отметить, что чем выше требования к качеству передачи информации, тем большее число спектральных составляющих следует учитывать.

Таким образом, ширина спектра ЧМ-колебания при неизменной амплитуде модулирующего напряжения остается постоянной, изменяется структура спектра сигнала.

При малом индексе модуляции m_ч << 1 полоса частот, занимаемая спектром, определяется наивысшим значением частоты модуляции, а не девиацией частоты. Модуляция при m_ч << 1 называется узкополосной частотной модуляцией.

Заключение. Передача информации на расстояние осуществляется с помощью несущих (ВЧ) колебаний, один или несколько параметров которых (амплитуду, частоту или начальную фазу) модулируют по закону сообщения.

По физическому смыслу модуляция является переносом спектра сообщения в область высоких частот. При угловой модуляции при переносе наблюдается трансформация спектра.

АМ-колебание занимает область частот вблизи частоты несущей, равную удвоенному значению максимальной частоты модулирующего сигнала. АМ сигнал обладает низкой помехоустойчивостью. Кроме того, в таком виде модуляции неэффективно используется мощность передатчика.

Сигналы с угловой модуляцией (ЧМ и ФМ) при больших значениях индексов модуляции занимают область частот, значительно превышающую ширину спектра модулирующего сигнала. Спектр сформированного сигнала существенно отличается от спектра модулирующего сигнала и является теоретически бесконечным, однако на практике его ограничивают. Условием для ограничения ширины спектра является качество передачи информации.

Сигналы с угловой модуляцией обладают рядом преимуществ перед сигналами с АМ: они имеют лучшую помехоустойчивость, кроме того более рационально используется мощность передатчика. Для достижения требуемой помехоустойчивости необходимо, чтобы девиация частоты была в 2 – 3 раза выше максимальной частоты спектра модулирующего сигнала. В России при высококачественном вещании при значении модулирующей частоты 15 кГц принята девиация частоты 50 кГц.

Вместе с тем для передачи таких сигналов требуется более широкая полоса выделяемых частот.

1. Какие сигналы являются ортогональными? 2. Что представляет собой ортонормированный базис функций? 3. Какие радиотехнические сигналы можно представлять рядами Фурье? 4. Какие формы рядов Фурье применяются в теории сигналов? 5. Какую информацию содержат амплитудный и фазовый спектры сигнала? 6. Почему для спектрального представления непериодических сигналов используют прямое преобразование Фурье, а не разложение в ряд Фурье? 7. Укажите размерность дискретного спектра и спектральной плотности сигнала. 8. Как связаны длительность простого сигнала с шириной спектра? 9. Какими основными свойствами обладает преобразование Фурье? 10. Что такое АКФ сигнала? 11. Какими свойствами обладает АКФ сигнала? 12. Как связаны спектральная плотность и АКФ сигнала?

Лекция 13