5. Вычисление портфельного риска

Портфель:

Coca-Cola - 65%

Reebok - 35%

Ожидаемая доходность акций

Coca-Cola - 10%

Reebok - 20%

Ожидаемая доходность портфеля – средневзвешенная ожидаемых значений доходности отдельных акций

0,65 х 10% + 0,35 х 20% = 13,5%

σ_Сoca-cola - 31,5%

σ_Reebok - 58,5%

Дисперсия для портфеля из двух видов акций равна сумме значений в ячейках, где Х₁ и Х₂ – доли инвестиций в акции 1 и 2 соответственно

	Акции 1	Акции 2
Акции 1	Х12 Ϭ 12	Х1Х2 Ϭ 12 = Х1Х2ρ12Ϭ1s2
Акции 2	Х1Х2 Ϭ 12 = Х1Х2 r12 Ϭ 1 Ϭ 2	Х22 Ϭ 22

Содержание синих ячеек зависит от дисперсии акций 1 и 2, содержание голубых ячеек зависит от их ковариации.

Ковариация служит мерой совместной изменчивости двух акций.

Ковариация акций 1 и 2 = σ ₁₂ = ρ ₁₂ σ ₁ σ ₂

ρ ₁₂ - коэффициент корреляции; σ₁₂ - коэффициент ковариации

Коэффициент корреляции изменяется в пределах от -1 до +1 и не имеет единицы измерения

1. Для большинства акций характерна тенденция к сопряженному изменению.

в этом случае ρ ₁₂ > 0, а значит и σ ₁₂ > 0.

2. Если различные акции изменяются вне всякой связи между собой, тогда ρ ₁₂ = 0 и σ ₁₂ = 0.

3. Если акции движутся в противоположных направлениях, то

ρ ₁₂ и σ ₁₂ – отрицательны.

Дисперсия портфеля = Х₁² σ ₁² +Х₂² σ ₂² + 2(Х₁ Х₂ ρ ₁₂ σ ₁ σ ₂)

Значение коэффициента корреляции, равное +1, говорит о наличии совершенной положительной связи между двумя акциями.

Дисперсия портфеля = (0,65)² х (31,5)² + (0,35)² х (58,5)² + 2(0,65 х 0,35 х 1 х 31,5 х 58,5) = 1676,9

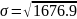
σ _{портфеля} = средневзвешенная σ _Сoca-cola и σ _Reebok

σ _{портфеля} = 0,65 х 31,5% + 0,35 х 58,5% = 41%

Так происходит, когда цены двух акций изменяются совершенно одинаково

Наибольший выигрыш диверсификация приносит, когда между акциями устанавливается отрицательная корреляция

Если r = -1, тогда

Дисперсия портфеля = (0,65)² х (31,5)² + (0,35)² х

х (58,5)² + 2(0,65 х 0,35 х (-1) х 31,5 х 58,5) = 0

= 0

При совершенной отрицательной корреляции всегда найдется портфельная стратегия позволяющая полностью исключить риск !

Коэффициент корреляции является основным показателем корреляционно-регрессионного анализа.

Корреляционно-регрессионный анализ - статистический метод, используемый для установления соотношений между зависимой переменной, и одной или более независимыми переменными.

Корреляционно-регрессионный анализ очень активно используется при анализе рынков ценных бумаг и анализе риска и прибыли, составляющих основу

теории портфельных вложений

6. Общая формула для вычисления портфельного риска

	1	2	3	4	5	6	7		N
1
2
3
4
5
6
7
N

Каждая выделенная ячейка содержит значение дисперсии, взвешенной по квадрату доли инвестиций в соответствующие ц/б.

В остальных ячейках – ковариация для каждых двух видов ц/б, взвешенная по произведению соответствующих долей инвестиций.

Ограничения на диверсификацию

Представьте портфель с равными долями инвестиций в N видов акций. Доля совокупных инвестиций в каждый вид акций равна 1/N. Значит, в каждой выделенной ячейке проставлено произведение (1/N)² на дисперсию σ ², а в любой другой - произведение (1/N)² на ковариацию.

Матрица состоит из N ячеек с дисперсий и (N² – N) ячеек с ковариацией, следовательно:

Дисперсия портфеля = N(1/N)² х средняя дисперсия + (N² – N) (1/N)² х средняя ковариация = (1/N) х средняя дисперсия + (1 - 1/N) х средняя ковариация

С увеличением числа акций N значение дисперсии портфеля постепенно приближается к среднему значению ковариации.

Средняя ковариация создает базовый риск, который остается даже после диверсификации портфеля.