Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Кафедра механизации, автоматизации и энергоснабжения строительства

Курсовой проект

на тему

Структурный анализ и синтез механизма

Выполнил: студент 1 курса

Гр. БЗТ-25

Малбасарова Н.Е.

Проверил:

к.т.н. Ленивцев А.Г.

САМАРА 2012 г.

Содержание

1. Структурный и кинематический анализ механизма…………………….3

1.1Структурный анализ и синтез механизма……………………………….3

1.2 Графический метод планов положений, скоростей и ускорений……..4

1.3 Метод кинематических диаграмм……………………………………….8

2. Проектирование и анализ зубчатых механизмов……………………….12

2.1 Параметры зубчатого зацепления………………………………………12

2.2. Порядок построения зубчатого зацепления…………………………...13

Список использованной литературы……………………………………….15

1. Структурный и кинематический анализ механизма

1.1 Структурный анализ и синтез механизма.

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, определение степени подвижности, статистической определимости и класса механизма.

Структурным синтезом механизма называется проектирование структурной схемы механизма, которая состоит из неподвижного и подвижных звеньев и кинематических пар.

С труктурной называется схема, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение.

На структурных схемах размеры звеньев не указываются. При указании размеров (длин) звеньев, координат неподвижных опор и масштаба построения схема становится кинематической.

Наиболее удобным методом получения структурной схемы является метод Ассура, по которому присоединяются структурные группы к стойке и к начальному (ведущему) звену или к основному механизму.

Начальное звено присоединено к стойке обычно шарниром или поступательной парой (рис 1.5) образует механизм 1 класса. Имеет одну степень подвижности W = 1.

Рисунок 1.5. Начальное звено.

Структурной группой Ассура называется кинематическая цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности, т.е. образует ферму.

Структурная формула группы Ассура W =3n -2p₅ = 0 ; p₅ = 3n/2

Возможны группы следующие составов

n = 2 ; 4 ; 6

p₅= 3 ; 6 ; 9

Простейшая структурная группа 2 класса, 2 порядка состоит из двух звеньев и трех кинематических пар. Возможны 5 видов простейших групп в зависимости от сочетания вращательных (В) и поступательных (П) пар.

В группах Ассура различают кинематические пары внутренние и внешние. Число внешних кинематических пар (вернее их элемен­тов), которыми группа присоединяется к другим звеньям механизма, называют порядком (числом поводков) группы. Наиболее простые структурные группы с п = 2 и p₅ = 3

Класс структурной группы определяется числом внутренних кинематичеcких пар, образующих наиболее сложный замкнутый контур группы.

При структурном анализе проводится расчленение механизма на структурные группы и начальные механизмы в порядке, обратном структурному синтезу. Из конца кинематической цепи механизма, принимая за её начало входное звено 1 последовательно отсоединяются группы II (4,5) и II (2,3) до тех пор, пока не останется ведущее звено на стойке - I (1,6):

I (1,6)  II (2,3)  II (4,5) (1.6)

Структурный анализ выполняется с целью правильного выбора методики кинематического и силового расчета механизма.

n3= n1/Uобщ = 55/2 = 27,5 об/мин

U12=3000/55=55,54 ; U34 = 36/12 = 3

w = Пn/30 = 3,14*27,5/30 = 2,88 1/c

1.2 Графический метод планов положений, скоростей и ускорений

Основные задачи кинематического анализа механизма состоят в определении перемещений, скоростей и ускорений его ведомых звеньев по заданному закону движения входного (ведущего) звена.

Среди графических методов наиболее распространены:

а) метод кинематических диаграмм, отражающих законы движения в виде графиков функций по времени: перемещения точки S_k = S(t), ее скорости V_k = V(t) и ускорения a_k = a(t);

б) метод планов положений, скоростей и ускорений.

Графические методы отличаются наглядностью, поэтому особенно приемлемы в учебных задачах, но менее точны. Однако степень точности достаточна для решения многих инженерных задач.

При графическом методе кинематического анализа механизмов длин звеньев, перемещения точек, их скорости и ускорения изображают в масштабах _e, _s, _v, _a.

Планом положений механизма называется графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени движения.

П остроим план положений кривошипно–шатунного механизма (рисунок 1.7), в масштабе _e = l_АВ / АВ (м/мм).

Рисунок 1.7. План положений механизма

Начальным или крайним называют положение звена, c которого начинается отсчет его движения в одном направлении.

Скорости точек и звеньев механизма определяются построением планов скоростей. Метод основан на графическом решении векторных уравнений скоростей.

Планом скоростей называется построенный в масштабе _v (м/с/мм) чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в рассматриваемый момент времени.

Для построения плана скоростей должны быть известны кинематическая схема, формула строения механизма и закон движения ведущего звена.

В качестве примера рассмотрим движение кривошипно–ползунного механизма (рис. 1.8). Для заданного положения ₁ механизма известны угловые скорости ₁ и ускорение ₁ ведущего звена. Требуется найти линейные скорости точек А, В, S₂ и угловую скорость звена 2.

Построение плана скоростей начинается с анализа движения входного звена – кривошипа 1 с переходом к анализу структурных групп по последовательности их присоединения. По формуле строения механизма I(1,4) II (2,3) начнем с определения скорости точки А звена 1, затем перейдем к определению скоростей точек В, S₂ и других точек присоединенной структурной группы 2 класса, состоящей из звеньев 2 и 3.

Скорость точки А кривошипа 1 можно описать уравнениями:

V_A1 =V_O1 +V_AO1=2,88* 0,25=0,72; V_A1= V_AO1=0,72 (1.8)

Так как точка О₁ неподвижна, то V₀₁ = О. Вектор V_AO1 направлен перпендикулярно кривошипу О₁ А, в направлении его вращения. Величина скорости (модуль вектора) точки А равна:

V_А = V_АО1 = l_O1A ^. ₁ (1.9)

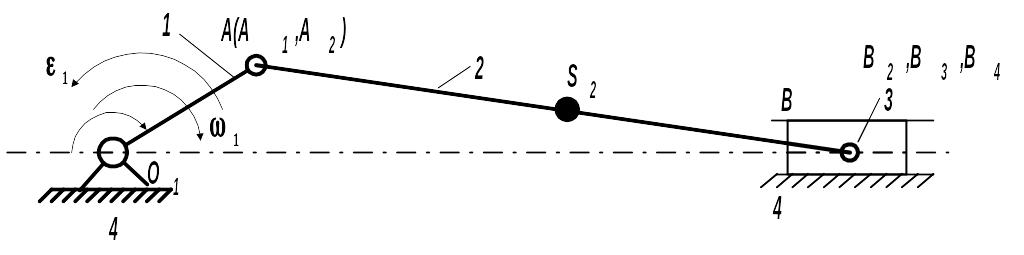
Рисунок 1.8. Кривошипно-ползунный механизм.

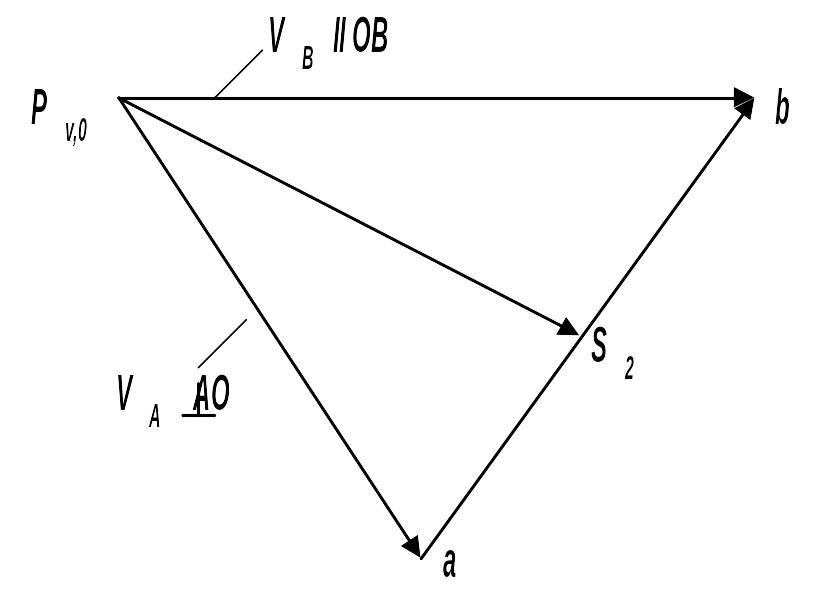
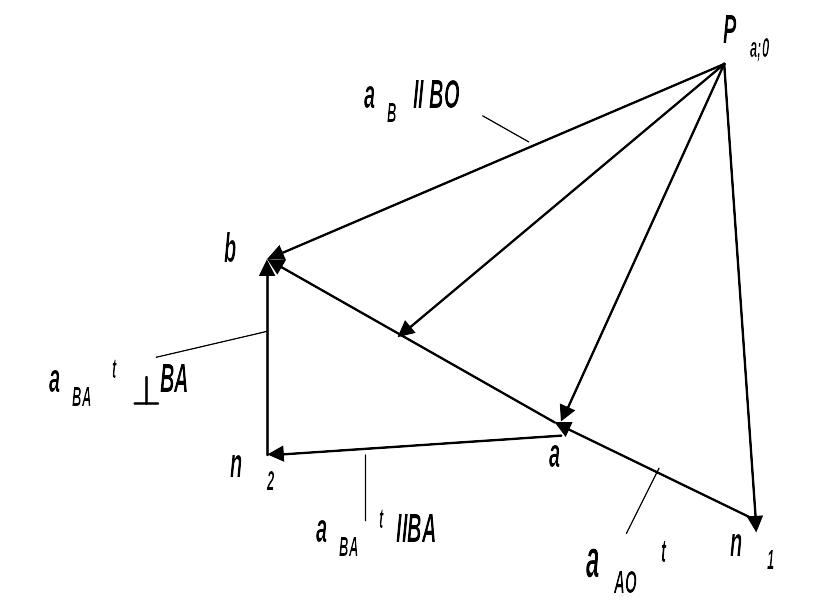
Рисунок 1.9. План скоростей и ускорений.

Из произвольного полюса p_V, выбранного вблизи схемы механизма, строим векторы по уравнению (1.7), принимая длину отрезка p_Vа = 30…100 мм. Тогда масштаб плана скоростей

_v = V_A / p_Vа =0,72/ 72=0,01 (м/с/ мм). (1.10)

Переходя к анализу структурной группы II (2,3), замечаем, что скорости точек А 1-го и 2-го звеньев одинаковы: V_A2 =V_A1 =V_A .

Точка В₂ , принадлежащая звену 2, рассматривается в относительном движении вокруг точки А, а В₃, принадлежащая звену 3, в движении относительно стойки 4. Поэтому запишутся уравнения :

 V_B2 =V_A2 +V_BA , (1.11)

1 VВ2	0	ω	0
2 VВ2	0,655	ω	0,262
3 VВ2	0,438	ω	0,1752
4 VВ2	0,72	ω	0,288
5 VВ2	0,432	ω	0,1728
6 VВ2	0,658	ω	0,2632
7 VВ2	0	ω	0
8 VВ2	0,658	ω	0,2632
9 VВ2	0,432	ω	0,1728
10 VВ2	0,72	ω	0,288
11 VВ2	0,438	ω	0,1752
12 VВ2	0,655	ω	0,262

Так какV_B =V_В2 =V_В3 , то V_A +V _ВА =V_B4 +V_B3B4 (1.12)

ВекторV_BА  ВА, а V_B3В4 ОВ. По уравнению (1.11) строим план скоростей. Из ранее принятого полюса p_V строим левую и правую части уравнения в виде отрезков, соответствующих скоростям точек V_А , из точки а проводим линию, перпендикулярную АВ в направлении скоростиV_ВА . При построении правой части уравнения в полюсе p_V отмечаем точку b₄ , так как V_В4 = 0, из нее проводим линию, параллельную ОВ в направлении V_В3В4. В пересечении указанных линий находим точку b. Вектором p_v b изображаем абсолютную скорость V_B точки В, а вектором ab – скорость V_ВА. Значения действительных скоростей находим по формулам,

V_B = _v ^. p_vb и V_BA = _v ^. ab (1.13)

Для определения скорости точки S₂ (центра масс звена 2) можно воспользоваться известной из теоретической механики теоремой подобия скоростей. Отрезки прямых линий, соединяющих точки на схеме звена механизма, и отрезки, соединяющие концы векторов относительных скоростей, образуют подобные и сходственно расположенные фигуры. Направление обхода aS₂b такое же как и фигуры АS₂В.

aS₂b  АS₂В. as₂ =ab . (1.14)

Отложив отрезок as₂ на отрезке ab плана скоростей и соединив точку S₂ с полюсом, построим вектор p_vS₂ абсолютной скорости точки S₂. Находим значение скорости точки S₂

V_S2 = _v ^. p_v S₂ . (1.15)

Угловая скорость звена 2 равна,

₂= V_ВА / l_BA = _v ^. ab / l_BA. (1.16)

Направление ₂ определяется по вектору ab скорости V_ВА . Оно против часовой стрелки в данном положении механизма.

Ускорения точек и звеньев механизма определяются построением планов ускорений.

Планом ускорений механизма называется чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в рассматриваемый момент времени.

Для построения плана ускорений должны быть известны кинематическая схема, формула строения механизма, закон движения ведущего звена и план скоростей. Рассмотрим движение кривошипно–ползунного механизма (рис. 1.8), где построен план скоростей.

Решение задачи выполняется на основе правила: абсолютное ускорение любой точки звена при плоском движении твердого тела равно геометрической сумме двух ускорений: ускоренияa_e в поступательном переносном движении и ускорения a_r во вращательном относительном движении:

a_a =a_e +a_r =a_e +a_rⁿ +a_r^ , (1.17)

гдеa_rⁿ иa_r^ - нормальное ускорение в относительном движении, направленное по радиусу вращения к центру кривизны траектории, и касательное ускорение, направленное перпендикулярно радиусу вращения.

По формуле строения механизма I (1,4)  II (2,3) построение плана ускорений начнем с определения ускорения точки А входного звена 1, затем перейдем к определению ускорений точек В и S₂ и построению векторов ускорений звеньев группы II (2,3).

Абсолютное ускорение точки А₁ по уравнению (11) равно

a_A1 =a₀ +a_A10ⁿ +a_A10^ , (1.18)

гдеa₀ – переносное ускорение точки О, равное нулю, так как точка неподвижна;

a_A10ⁿ - нормальное (центростремительное) ускорение точки А₁ относительно точки О, направленное к центру О, т.е. II АО;

a_A10ⁿ = ₁^{2 .} l_AO =2,88²*0,25 = 2,07 м/с2 (1.19)

a_A10^ - касательное (тангенциальное) ускорение точки А₁ относительно точки О, направленное перпендикулярно АО, в сторону ₁ ,

так как a_A10^ =₁^. l_AO (1.20)

Из произвольного полюса р_а (рисунок 1.9), выбранного вблизи схемы механизма, строим векторы по уравнению (1.18), принимая длину отрезка р_аn₁ = 30…100 мм и определив масштаб плана ускорений:

_а = a_A10ⁿ / р_аn₁ = м/с^{2 .} мм. (1.21)

Построив из точки О, совпадающей с р_а, так как а₀ = 0, отрезок оn₁ ускорения a_A10ⁿ , проведем отрезок n₁а = a_A0^ / _а касательное ускорение a_A0^ . Соединяя полюс р_а с точкой а, находим полное ускорение точки А₁ (отрезок р_аа):

а_А =_а ^. р_аа . (1.22)

Переходя к анализу структурной группы II (2,3), запишем уравнения ускорения точки В:

a_В =a_а +a_ВА ; a_В =a_В4 +a_В3В4 ; (1.23)

a_A +a_ВАⁿ +a_ВА^ =a_В4 +a_В3В4 . (1.24)

Значение нормальной составляющей относительного ускорения определяется по формуле:

a_ВАⁿ = ₂^{2 .} l_ВА.= 1,63² * 0,4 = 1,06 м/с² (1.25)

Вектор a_ВАⁿ направлен по АВ к центру вращения (точке А) и откладывается из точки а плана. Длина отрезка an₂ = a_ВАⁿ / _а . Направлениеa_ВА^ будет проходить через конец вектора a_ВАⁿ и перпендикулярно ВА. При построении правой части уравнения (17) отмечаем в полюсе р_а точку b₄. Так как a_В4= 0, из нее проводим линию, параллельную ОВ в направленииa_В3В4. Пересечение этой линии с перпендикуляром к ВА определит положение точки b на плане, а следовательно, величину ускорения

а_В = _а ^. р_аb . (1.26)

Вектор аb изображает полное относительное ускорение а_ВА .

Угловое ускорение звена 2 находим из уравнения

. (1.27)

Перенеся векторn₂b в точку В и рассматривая действие вектора относительно точки А, находим направление ₂ , против часовой стрелки в данном случае.

По подобию фигур aS₂b  АS₂В определяем величину абсолютного ускорения точки S₂ , как при определенииV_S2 . Отрезок аs₂ = ab (AS₂ / AB) отложим на отрезке аb, соединим точку S₂ с полюсом р_а , тогда

a_s2 = _а ^. р_а S₂ . (1.28)

Для кинематического анализа механизма за весь цикл (полный оборот входного звена) выполняется построение планов скоростей и ускорений в 12 последовательных положениях входного и других звеньев.