Оценка погрешностей приближенных методов

Оценка погрешности приближенного решения хк, найденного методом простой итерации, имеет вид:

, (8)

где х* - точное (искомое) решение СЛАУ (1).

Левая часть неравенства (8) есть абсолютная погрешность приближения х^к.

Правая часть (8) есть предельная абсолютная погрешность.Неравенство (8) можно использовать для решения двух задач:

1.Найти предельную абсолютную погрешность приближения х^k.

2. Найти величину, позволяющую останавливать процесс итераций в автоматическом режиме, если задана точность ε, с которой требуется найти приближенное решение.

Пример. Пусть

Отсюда следует, что процесс итераций для заданной линейной системы уравнений сходится.

Пусть СЛАУ с этой приведенной матрицей надо решить с абсолютной погрешностью ∆х=0,005.

Из (8) следует:

Рассмотрим решение задачи 2 в общем виде.Пусть требуется найти решение СЛАУ хk с

точностью ε, т.е.

Тогда с учетом (8) получаем:

(9)

где – норма матрицы А, определяемая выражением:

Из неравенства (9) следует:

(10)

Неравенство (10) должно проверяться на каждой итерации. Как только оно будет выполнено, итерационный процесс должен быть остановлен, так как требуемая точность ε достигнута.

Оценка погрешности для метода Зейделя имеет вид:

где

Метод Халецкого

Рассмотрим СЛАУ вида : A·x=b (1)

где A – квадратная матрица порядка n. Обозначим:

a_{1 n}+1

a_{2 n}+1

b = ……

a_{n n}+1

В теории Высшей алгебры доказано, что почти всякую квадратную матрицу можно представить в виде произведения двух треугольных:

A = B · C, (11)

b₁₁ 0 … 0

b₂₁ b₂₂ …0

где B = ………….

b_n1 b_n2 …b_nn

1 c₁₂ … c_1n

0 1 … c_2n

C = ………………

0 0 … 1

Исходя из соотношения (11), можно найти выражения для

вычисления элементов матриц A и B:

b_i1 = a_i1

(12)

(13)

С учетом (11) система уравнений (1) примет вид:

(14).

Обозначим (15),

Тогда (16).

В силу треугольности матриц В и С, решение систем (15 ) и (16) представлено в явном виде:

(17)

и

(18)

Этот метод получил название схемы Халецкого. В схеме применяется обычный контроль с помощью сумм. Над столбцом сумм производим те же действия, что и над столбцом свободных членов.

Пример:

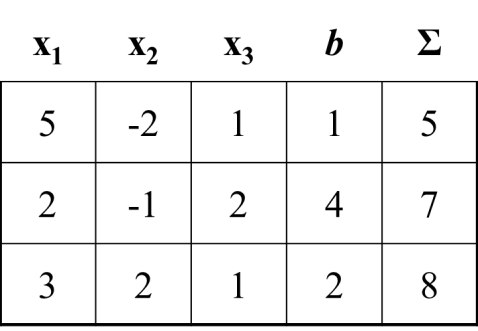
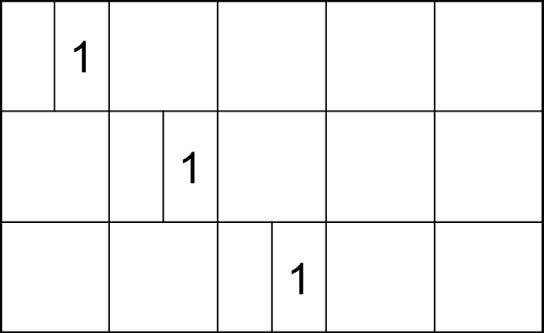
1. i=1, 2, 3

2. j=2, 3,4,5

3. j=2 i=2, 3

i=2 -1-2(-0.4)=-0.2

i=3

4. i=2 j=3, 4, 5

j=3

5. j=3

i=3

О точности точных и приближённых методов

Если все элементы системы (1) имеют m верных знаков после запятой, то итерационные процессы позволяют найти решение с m верными знаками в дробной части.

Если все элементы системы (1) точные числа, то и решение приближёнными методами может быть найдено с любой заданной точностью.

Для проверки точности решения (1), найденного точным методом, надо подставить его в (1):

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦ

Рассмотрим квадратную матрицу А=[aij], i, j=1,2,…,n и n-мерный вектор х≠0.

Определение. Вектор х≠0 называется собственным вектором матрицы А, если найдется число λ такое, что имеет место равенство:

(1)

Число λ в (1) называется собственным значением или характеристическим числом матрицы А, соответствующим собственному вектору х.

Теорема. (О существовании собственных векторов).В комплексном векторном пространстве каждая матрица имеет по меньшей мере один действительный или комплексный собственный вектор.

Рассмотрим алгоритм нахождения собственных элементов нормальной (симметричной и положительно определенной) матрицы.

Если матрица нормальная, то ее собственные элементы обладают двумя важными свойствами:

1.Собственные числа λ1, λ2,…, λn ее действительны и положительны;

2. Собственные векторы хi, i=1,2,…,n действительны и взаимно ортогональны:

при j≠k.

Исходя из доказательства теоремы существования, первый собственный вектор х1 и соответствующее собственное число λ1 определяются из системы линейных уравнений:

(2)

Определитель системы (2) равен 0.

Приведем эту систему к виду, необходимому для итерационного процесса:

(3.3)

Так как координаты собственных векторов определяются с точностью до множителя пропорциональности, то одна из них произвольная, для определенности возьмем =1. Систему (3) можно решать и методом итераций, и методом Зейделя.

Для определения λ2 и х2 можно решить систему:

Из соотношения ортогональности векторов х1 и х2:

исключаем одну из компонент вектора х2, например, . Тогда система

для определения λ2 и х2 примет вид:

(4)

Полагая =1, решим систему (4) и тем самым найдем λ2 и х2.

Пример. Дана

Найти х1 и λ1.

Данная матрица симметричная и положительно определенная. Последнее

следует из того, что:

Составим аналог системы (3.2):

Преобразуем ее к виду (3.3), при =1:

Эту систему можно решить методом итерации. Начальное приближение

возьмем: , ,

Решив систему, получим: