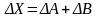Теория погрешностей.

Виды погрешностей:

Систематические погрешности связаны либо с точностью прибора, либо метода измерений, либо с невозможностью учета некоторых факторов.

Случайные погрешности вызываются большим числом случайных факторов, действие которых на каждое отдельное измерение различно и не может быть заранее учтено.

Грубые погрешности возникают в результате просчета, неправильной корреляции и т.д. Результаты расчетов на основе измерений, содержащих грубые ошибки, существенно отличаются от других и поэтому могут быть замечены при тщательном анализе модели. Их обычно исключают.

Ошибкой или погрешностью ∆ а приближенного числа а называется разность между точным числом А и его приближением:∆а=А-а

На практике чаще пользуются абсолютной погрешностью приближенного числа а: ∆^а=|∆а|=|А-а|

Предельной абсолютной погрешностью ∆_а приближения а называется всякое число, не меньшее абсолютной погрешности этого числа: ∆_а ≥ ∆^а

Интервал для точного числа А:

а-∆_а ≤ А ≤ а+∆_а. (1.1)

Относительной погрешностью δ^а приближения а называется отношение абсолютной погрешности ∆^а этого числа к модулю соответствующего точного числа А (А ≠ 0):

Отсюда ∆_а=δ^а•|А|

Предельной относительной погрешностью δ_a приближения а называется всякое число, не меньшее относительной погрешности этого числа: δ^a ≤ δ_{a ,}т.е. ,отсюда ∆а≤|A|• δ_a.

Таким образом, за ∆_a можно принять: ∆_а≈|a|• δ_a. Зная δ_a и используя формулу

a-∆_a ≤ A ≤ a+∆_a, напишем интервал точного числа А через предельную относительную погрешность: а•(1- δ_a) ≤ А ≤ а•(1+ δ_a) (1.2)

Верные знаки

Всякое положительное десятичное число а может быть представлено в виде:

а=α_m•10^m+α_m-1•10^m-1+…+α_m-n+1•10^m-n+1+…, где α _i-цифры числа а, причем старшая цифра α_m≠0, а m-некоторое целое число (старший десятичный разряд числа а ).

Если для приближенного числа а, заменяющего точное число А, известно, что ∆а=|A-a|≤½•10^m-n, то по определению, первые n цифр а_m, а_m-1, а_m-n+1 этого числа верные.

Математическая операция	Абсолютная погрешность	Относительная погрешность

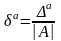
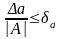
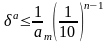
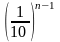
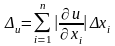
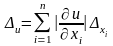
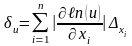
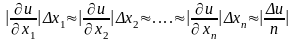
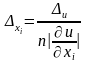
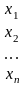
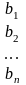
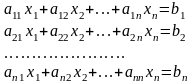
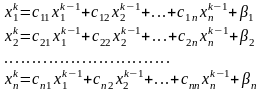
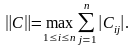
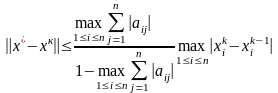
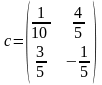
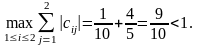
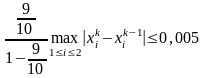
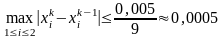
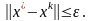
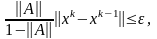
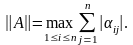
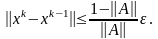
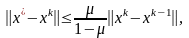
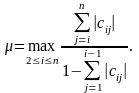
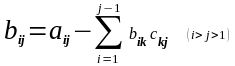
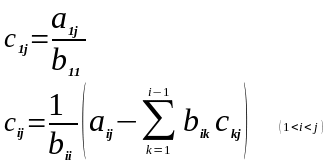
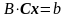
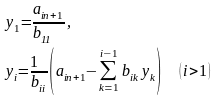
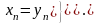
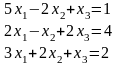
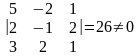
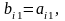
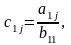
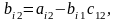
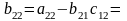
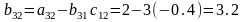
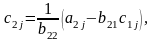
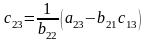
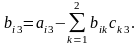
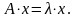
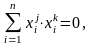
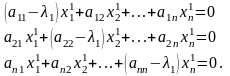
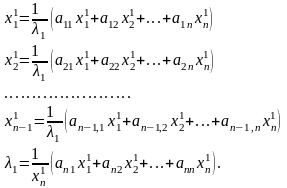
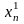
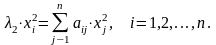
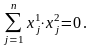
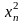
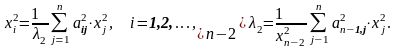
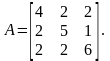
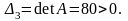
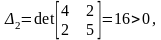
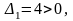
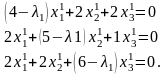
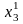
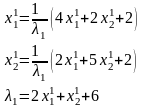
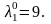
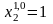
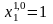
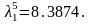
Теорема. Если положительное приближенное число а имеет n верных десятичных знаков, то относительная погрешность δ^a этого числа не превосходит , деленную на первую значащую цифру данного числа, т.е.
, (1.3)

где α_m-первая значащая цифра числа а.

Формулы для подсчета абсолютной и относительной погрешностей косвенных измерний.

Общая формула для погрешности косвенных измерений.

Известны погрешности аргументов некоторой функции u=f(x₁, x₂,…, x_n), требуется определить погрешность этой функции. Пусть задана дифференцируемая функция u=f(x₁, x₂,…, x_n) и пусть известны |∆x_i|, i=1,2…,n - абсолютные погрешности аргументов. Тогда предельная абсолютная погрешность функции

(1.4)

Разделив обе части равенства

на |u| ,получим предельную относительную погрешность функции u:

1.5

Обратная задача.

Каковы должны быть абсолютные погрешности аргументов функции, обеспечивающие вычисление функции u с погрешностью ∆_u, не превышающей заданной величины. Пусть:

Из формулы следует i=1,2,…,n

Линейная алгебра

Методы решения систем линейных уравнений (СЛУ) делятся на две группы:

1.Точные методы. Представляют собой конечные алгоритмы нахождения корней системы (таковы, например, метод Гаусса, правило Крамера, метод Халецкого и д.р.)

2.Итерационные методы. Они позволяют получать корни системы с заданной точностью путем построения конечной, а чаще бесконечной последовательности приближений, итераций (к их числу относятся метод простых итераций, метод Зейделя, метод релаксаций и др.).