6.4. Интервальные оценки. Доверительный интервал

Точечная оценка параметров генеральной совокупности является лишь приближенным значением неизвестного параметра и для выборки малого объема

_{может существенно отличаться от него. Чтобы иметь представление о точности и надежности оценки параметра используют интервальную оценку параметра.}

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал , который с заданной вероятностью (надежностью) покрывает заданный параметр. Вероятность называется доверительной вероятностью, уровнем доверия или надежностью оценки.

Величина доверительного интервала зависит от объема выборки (уменьшается с ростом ) и от значения доверительной вероятности (увеличивается с приближением к единице).

Часто интервал выбирают симметричным относительно параметра , т.е. выбирают интервал .

Отклонение оценки от оцениваемого параметра называется точностью оценки: .

Любую точность можно получить с определенной вероятностью (надежностью):

.

Это условие означает, что интервал покрывает значение параметра с заданной доверительной вероятностью . Точность оценки фактически определяет длину доверительного интервала (2 ).

Построение доверительного интервала для генеральной средней и генеральной доли по большим выборкам основано на следующей теореме

Теорема. Вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число >0 (по абсолютной величине), равна:

, где ; , где , – функция Лапласа. Для вычисления значений этой функции для положительных значений составлена таблица (приложение 2) ; для значений полагают . Для отрицательных значений используют ту же таблицу, учитывая, что функция Лапласа нечетная: .

Доверительный интервал для среднего значения

нормального распределения при известном .

Интервальной оценкой с надежностью математического ожидания нормально распределенного признака по выборочной средней является доверительный интервал

,

где – точность оценки, – объем выборки, – значение аргумента функции Лапласа , при котором .

Доверительный интервал для среднего значения нормального

распределения при неизвестном (и объеме выборки ).

Интервальной оценкой с надежностью математического ожидания нормально распределенного признака в этом случае служит интервал ,

где – «исправленное» выборочное среднее квадратическое отклонение ( ); находится по заданным и по таблице (см. приложение 3).

Доверительный интервал для дисперсии нормального распределения

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного признака по «исправленному» выборочному среднему квадратическому отклонению служит доверительный интервал

< < при ( < 1),

0 < < при ( > 1),

где находят по таблице по и .

Определение объема выборки

Для определения объема выборки необходимо задать надежность ( доверительную вероятность) оценки и точность (предельную ошибку выборки) .

Для повторной выборки при оценке генеральной средней с надежностью искомый объем выборки вычисляется по формуле

, где , – функция Лапласа.

Если найден объем повторной выборки , то объем соответствующей бесповторной выборки находится по формуле .

Задачи

18.. Найти доверительный интервал для оценки с надежностью 0, 95 неизвестного математического ожидания нормально распределенного признака генеральной совокупности, если генеральное среднее квадратическое отклонение , выборочная средняя , а объем выборки .

Решение. Требуется найти доверительный интервал

.

Все величины, кроме , известны. Найдем из соотношения По таблице значений функции Лапласа (приложение 2, табл.1) находим =1,96. Поставив значения =1,96, , , в формулу, получим искомый доверительный интервал 12,04 < а < 15,96.

19. а) Найти доверительный интервал для оценки с надежностью 0, 99 неизвестного математического ожидания нормально распределенного признака генеральной совокупности, если генеральное среднее квадратическое отклонение , выборочная средняя , а объем выборки .

b) Та же задача при условии, что , , .

20. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы оказалась равной 1000 часов. Найти с надежностью 0, 95 доверительный интервал для средней продолжительности горения лампы всей партии, если среднее квадратическое отклонение продолжительности горения лампы часов. Предполагается, что продолжительность горения ламп распределена нормально.

21. Станок–автомат штампует валики. По выборке объема вычислена выборочная средняя диаметров изготовленных валиков. Найдите с надежностью 0,95 точность , с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков., зная, что их среднее квадратическое отклонение . Предполагается, что диаметры валиков распределены нормально.

22. Найти минимальный объем выборки, при котором точность оценки математического ожидания генеральной совокупности по выборочной средней равна с надежностью 0, 975. Среднее квадратическое отклонение нормально распределенной генеральной совокупности .

Решение. Воспользуемся формулой, определяющей точность оценки ожидаемого математического ожидания генеральной совокупности по выборочной средней: . Отсюда . По условию, . Поэтому . По таблице значений функции Лапласа найдем . Подставив значения , , в формулу для вычисления , получим .

23. Найдите минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределенной генеральной совокупности по выборочной средней равна 0,2. Среднее квадратическое отклонение генеральной совокупности .

24. Из генеральной совокупности извлечена выборка объема :

варианта -2 1 2 3 4 5

частота 2 1 2 2 2 1

Оценить с надежностью 0, 95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

Решение. Выборочную среднюю и «исправленное» среднее квадратическое отклонение найдем по формулам: 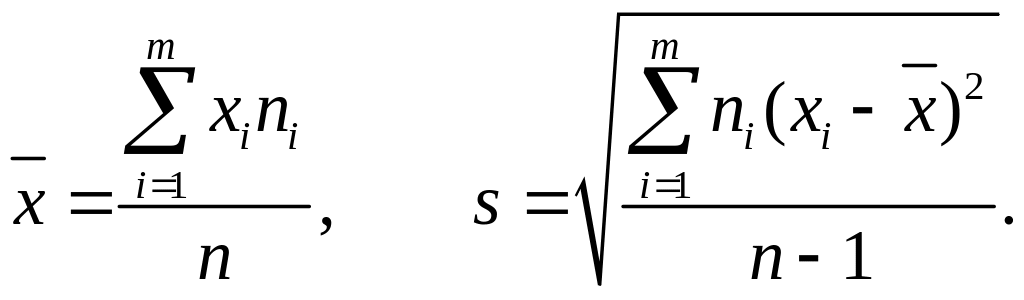Подставив в эти формулы данные задачи, получим .

Найдем , пользуясь таблицей для вычисления по значениям и . Итак, . Найдем искомый доверительный интервал:

.

Подставляя , , в эту формулу, получим искомый интервал , покрывающий неизвестное математическое ожидание с надежностью 0,95.

25. Из генеральной совокупности извлечена выборка объема :

варианта –2 1 2 3 4 5

частота 2 1 2 2 2 1

Оценить с надежностью 0, 95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

26. По данным девяти независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений и «исправленное» среднее квадратическое отклонение . Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью . Предполагается, что результаты измерений распределены нормально.

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию a. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала .

Все величины, кроме , известны. Найдем , пользуясь таблицей для вычисления по значениям и : . Подставив , , , в формулу для интервала, получим искомый интервал: .

27. По данным шестнадцати независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений и «исправленное» среднее квадратическое отклонение . Оцените истинное значение измеряемой величины с помощью доверительного интервала с надежностью . Предполагается, что результаты измерений распределены нормально.

28. По данным выборки объема из генеральной совокупности найдены «исправленное» среднее квадратическое отклонение нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью .

Решение. Задача сводится к отысканию доверительного интервала (если ) или (если ).

По данным и по таблице значений q найдем . Так как , то подставив и в первую из указанных формул, получим искомый доверительный интервал .

29. По данным выборки объема n из генеральной совокупности нормально распределенного количественного признака найдены «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,999, если: а) , ; б) , .