6. Элементы математической статистики

Математическая статистика – это наука, занимающаяся получением, описанием и обработкой опытных данных или наблюдений с целью изучения закономерностей массовых явлений.

6.1. Вариационные ряды и их графическая интерпретация

В практике статистических наблюдений различают два вида наблюдений: сплошное, когда изучаются все объекты (элементы) и выборочное, когда изучается часть объектов. Вся изучаемая совокупность объектов называется «генеральной совокупностью». Простейший пример генеральной совокупности – материалы переписи населения той или иной страны, в которых имеются сведения о всех ее гражданах. Понятие генеральной совокупности аналогично понятию всей совокупности значений случайной величины.

Как правило, для обработки наблюдений или опыта удается использовать только часть генеральной совокупности – так называемую «выборочную совокупность» или «выборку».

Сущность выборочного метода в статистике состоит в том, чтобы по свойствам выборки сделать вывод о свойствах всей генеральной совокупности.

На начальном этапе данные выборки заносятся в таблицу, где записываются номера и результаты измерений или опросов. Различные значения случайной величины, наблюдаемые в результате эксперимента, называются вариантами (обозначаются через x). В таблице варианты располагаются в порядке их возрастания.

Пример. Генеральная совокупность – N ящиков с приборами;

Выборочная совокупность – n = 10 выбранных для контроля ящиков.

Подсчитывается число пострадавших при транспортировке ящиков деталей. Результаты подсчета представлены в таблице:

№ ящ.	1	2	3	4	5	6	7	8	9	10
Кол. д.	0	1	4	1	2	3	1	5	0	2

Если количество пострадавших деталей – это изучаемая случайная величина X, то полученные данные о ней можно представить в виде «статистического ряда распределения»:

Х	0	1	2	3	4	5
	0,2	0,3	0,2	0,1	0,1	0,1

Здесь, как для любой дискретной случайной величины, перечислены все возможные значения, принимаемые величиной Х, но вместо вероятностей этих значений во второй строке записаны их относительные частоты . Например, пострадавших деталей нет только в двух ящиках (в первом и девятом) из десяти, поэтому и . Заметим, что вместо относительных частот можно использовать также число , которое показывает, сколько раз данная варианта встречается в выборке; это число называют частотой варианты.

Расположенный в порядке возрастания (или убывания) ряд вариант с соответствующими им частотами или относительными частотами называется вариационным рядом.

Возможен и другой способ описания статистических данных. Пусть мы опять имеем «статистический ряд», но достаточно длинный. Чтобы сделать результаты опыта более обозримыми, весь диапазон наблюденных значений величины разобьем на разряды (интервалы) и подсчитаем частоту попадания значений в соответствующий интервал. Рассмотрим опять наш пример.

Интервал значений Х	0 Х < 2	2 Х 3	3 Х 5
Частота попаданий в интервал	5 ( 0,5)	2 ( 0,2 )	2 ( 0,2 )

В скобках указаны относительные частоты.

При составлении вариационного ряда по интервалам следует иметь ввиду, что число интервалов следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака . Все интервалы желательно выбирать одинаковой длины, при этом начало интервала включается в него, а конец – нет. Согласно формуле Стерджеса рекомендуемое число интервалов , а величина (ширина интервала) , где – разность между наибольшим и наименьшим значениями признака.

При изучении вариационных рядов наряду с понятием частоты используется понятие накопленной частоты (обозначение ). Накопленная частота показывает, сколько наблюдалось вариантов со значением признака, меньшим . Отношение накопленной частоты к общему числу наблюдений называют накопленной частоты .

Накопленные частоты для каждого интервала находятся последовательным суммированием частот всех предшествующих интервалов, включая данный.

Для графического изображения вариационных рядов используются два вида графиков: полигон частот или относительных частот и гистограмма.

Полигон частот (относительных частот) представляет собой ломаную, отрезки которой соединяют точки с координатами (или координатами ( )) , где –значения исследуемой случайной величины.

Д

0,3

ля рассмотренного выше вариационного ряда полигон относительных частот имеет следующий вид:

5

П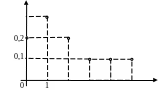 олигон частот является аналогом многоугольника распределений дискретной случайной величины.

Гистограммы служат только для изображения интервальных вариационных рядов.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы значений признака, а высоты равны отношению (то есть определяются количеством значений измеряемой величины, попадающих в соответствующий интервал). Площадь i-го прямоугольника равна – сумме частот вариант, попавших в i-й интервал.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы значений признака, а высоты равны отношению . Площадь i-го прямоугольника равна – относительной частоте вариант, попавших в i-й интервал.

Г истограмма нашего интервального вариационного ряда изображена ниже.

Если соединить середины верхних оснований прямоугольников отрезками, то получится полигон того же распределения.

Еще одним важным понятием служит понятие эмпирической функции распределения.

Эмпирической функцией распределения называется относительная частота того, что признак (случайная величина ) примет значение, меньшее заданного , то есть

.

Согласно этому определению, для данного эмпирическая функция распределения представляет накопленную частость :

.