3.3.3. Некоторые практические приложения понятия производной

Понятие производной находит практические приложения не только внутри математики. Оно широко используется в физике, технике, биологии, экономических и социологических исследованиях. В школьном курсе математики с помощью производной исследуются такие свойства функции, как ее монотонность, наличие локальных экстремумов, точек перегиба графика функции, находятся промежутки выпуклости и вогнутости графика, т.е. свойства, которые с определенной степенью точности позволяют изобразить эскиз графика на координатной плоскости. Мы не будем здесь рассматривать эти вопросы. Остановимся лишь на тех применениях, которые опираются на механический смысл производной.

Механический смысл производной. Если точка движется по закону , где – путь, – время, то представляет скорость движения в момент времени . Вторая производная от функции по времени есть скорость изменения скорости, то есть ускорение точки в момент времени

В общем случае производную функции , описывающей зависимость величины y от величины x, можно интерпретировать как «скорость» изменения величины y по отношению к величине x. Так, например, в экономике рассматриваются предельные характеристики экономических объектов или процессов, которые характеризуют не состояние, а скорость изменения экономического объекта или процесса относительно времени или другого исследуемого фактора. Рассмотрим некоторые из предельных величин, используемых в настоящее время в экономике.

1. Издержки производства. Пусть издержки производства являются некоторой функцией от количества выпускаемой продукции: . Тогда производная будет выражать предельные издержки производства и приближенно характеризовать прирост переменных затрат на производство дополнительной единицы продукции. Заметим, что средние издержки являются издержками на единицу выпуска продукции: .

2. Производительность труда. Пусть функция выражает объем произведенной продукции за время . Тогда производная этой функции выражает производительность труда в момент времени .

3. Функции потребления и сбережения. Пусть – национальный доход, – функция потребления (часть дохода, которая тратится), а – функция сбережения. Тогда .

Дифференцируя правую и левую части равенства по , получим:

,

где – предельная склонность к потреблению, а – предельная склонность к сбережению.

4. Эластичность функции. Это – мера реагирования одной переменной величины на изменение другой. Эластичность функции показывает, на сколько процентов изменится одна переменная в результате изменения другой переменной на 1% и определяется формулой:

.

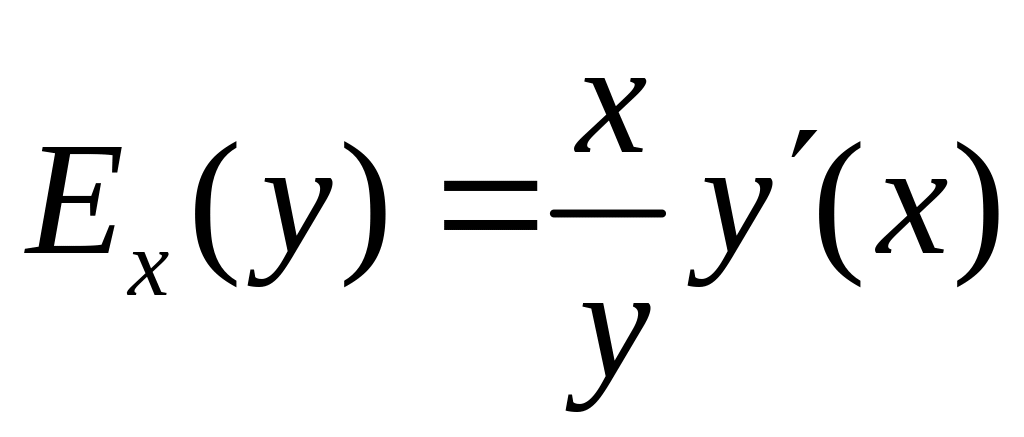Заметим, что эластичность функции часто применяют при анализе зависимости спроса и предложения от цены. В этом случае она показывает, на сколько процентов приближенно изменится спрос или предложение при изменении цены на 1%. Если эластичность спроса , то спрос считается эластичным, если , то – нейтральным, а если , то – неэластичным относительно цены.

Задачи

132. Функция издержек производства продукции некоторой фирмой имеет вид: (ден.ед.). Найти средние и предельные издержки производства и вычислить их значение при .

Решение. Найдем производную заданной функции: . Полученная функция определяет предельные издержки производства. Их значение при равно .

Средние издержки данного производства вычисляются следующим образом : ,

.

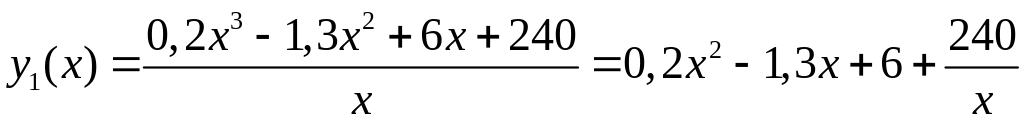Это значит, что при данном уровне производства средние затраты на изготовление одной единицы продукции составляют 37 ден ед., а увеличение объема на одну единицу обойдется фирме приближенно в 40 ден. ед..

133. Функция потребления некоторой страны имеет вид: , где – совокупный национальный доход (ден. ед.). Найти: 1) предельную склонность к потреблению; 2) предельную склонность к сбережению, если национальный доход составляет 27ден. ед.

Решение. Найдем предельную склонность к потреблению: ; ее значение при равно ден. ед.. Так как , то предельная склонность к сбережению . ее значение при равно .

134. Объем производства мужских костюмов, выпускаемых некоторой фабрикой, может быть описан следующей функцией (ед.), где – календарный месяц года. Вычислить производительность труда, скорость и темп ее изменения: а) в начале года ; б) в середине года ; в) в конце года .

Решение. а) Производительность труда выражается производной

(ед./мес.). Скорость и темп изменения производительности выражается , соответственно, производной функции и логарифмической производной ее: (ед./ мес².); и 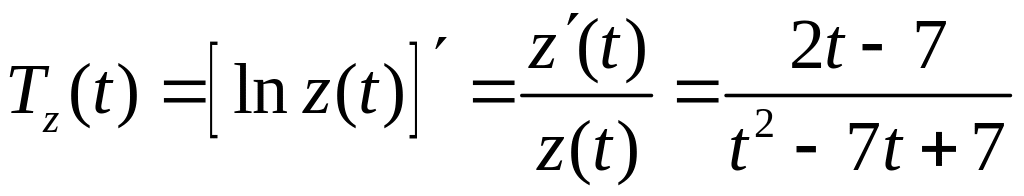(ед./мес.). В заданные моменты времени имеем соответственно: а) (ед./мес.), (ед./мес².) (ед./мес.).

б) (ед./мес.), (ед./мес².), (ед./мес.). в) (ед./мес.), (ед./мес².), (ед./мес.).

135. Зависимость между издержками производства и объемом выпускаемой продукции на некотором предприятии выражается функцией . Определите средние и предельные издержки при объеме продукции 10 ед. 45, 35.

136. Выручка от продажи конфет составляет , где – объем проданной продукции (тыс. ед.). Найдите среднюю и предельную выручки, если продано а) 10 тыс. ед; б) 60 тыс. ед. а) 95, 90 ; б) 70, 40.

137. Себестоимость продукции связана с объемом выпускаемой продукции уравнением . Определите среднюю и предельную себестоимость продукции при объеме, равном 10 ед. 2,06; 0,58.

138. Производительность труда бригады описывается уравнением , где – рабочее время, выраженное в часах. Вычислите скорость и темп изменения производительности труда при и . При , ; , .

139. Функции потребления некоторой страны имеет вид: , где – совокупный национальный доход (ден. ед.). Найдите: 1) предельную склонность к потреблению; 2) предельную склонность к сбережению, если национальный доход составляет 27ден. ед. 1) 2)

140. Функции сбережения некоторой страны имеет вид: , где – совокупный национальный доход (ден. ед.). Найдите: 1) предельную склонность к потреблению; 2) предельную склонность к сбережению, если национальный доход составляет 27ден. ед. ( )

141. Зависимость между себестоимостью (млн руб)готовой продукции предприятия и объемом выпускаемых изделий (тыс. шт.) выражается уравнением . Найдите эластичность себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции.

142. Зависимость между объемом выпуска готовой продукции (млн руб.) и объемом производственных фондов (млн руб.) выражается функцией . Найдите эластичность выпуска продукции для предприятия, имеющего фонды в размере 40 млн руб.