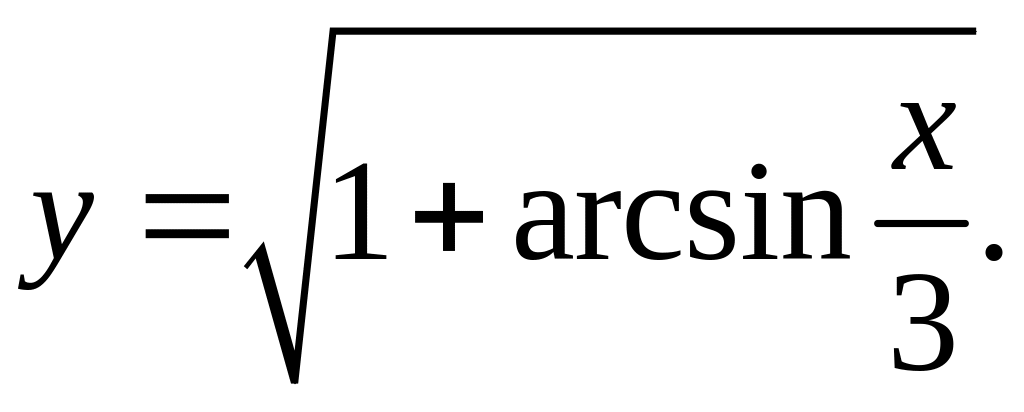3.3.2. Таблица производных основных элементарных функций.

Дифференцирование элементарных функций.

В левом столбце следующей ниже таблицы приведены формулы для производных основных элементарных функций, в правом столбце – следствие из них и из правила дифференцирования сложной функции.

№		, где
1
2
2а
2в
3
4
5
6
7
7а
8
8а
9
10
11
12

Пользуясь этой таблицей и правилами дифференцирования, можно продифференцировать любую элементарную функцию.

Задачи

69. . Найти .

Решение. Запишем формулу как сумму двух степенных функций и воспользуемся правилом дифференцирования суммы и формулой 2 из таблицы производных:

.

69. Найти

Решение. Применим сначала правило дифференцирования произведения функций, а затем воспользуемся формулами 2 и 3 из таблицы производных:

.

69. Найти .

Решение. Сначала применим правило дифференцирования частного функций, а затем – формулы 2 и 7а из таблицы производных:

69. . Найти .

Решение. Данная функция сложная. Она получена композицией двух функций: и Используя правило дифференцирования сложной функции, правило дифференцирования суммы и правила 2а будем иметь:

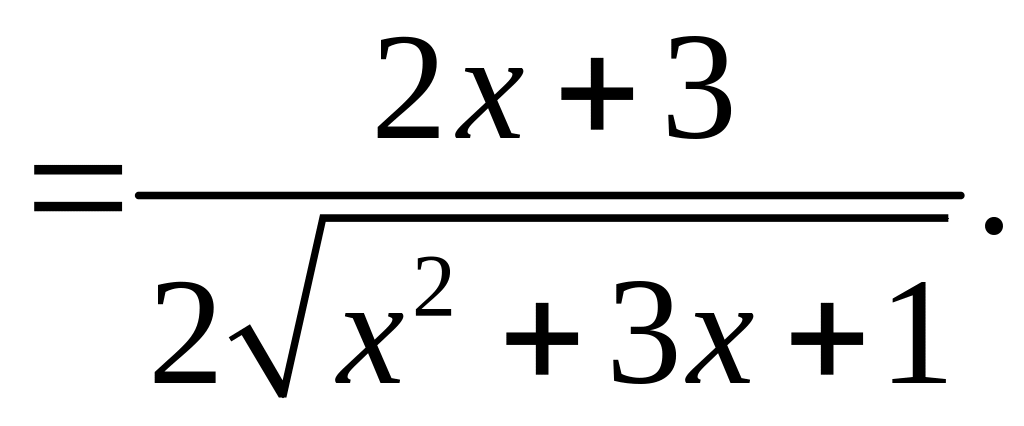
Вспомогательную функцию u(x) при дифференцировании сложной функции можно вводить мысленно.

69. Найти .

Решение. Введя (мысленно) функцию получим

69. Найти .

Решение. Введя мысленно функции и , композицией которых является данная функция, получим по правилу дифференцирования сложной функции:

При надлежащем навыке дифференцирования все промежуточные действия выполняются в уме, а решение записывается следующим образом:

69. . Найти .

Решение. По правилу дифференцирования сложной функции , где , , получим: .

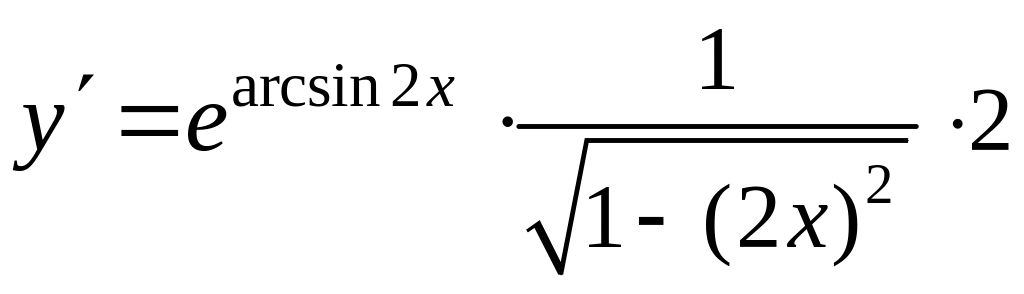
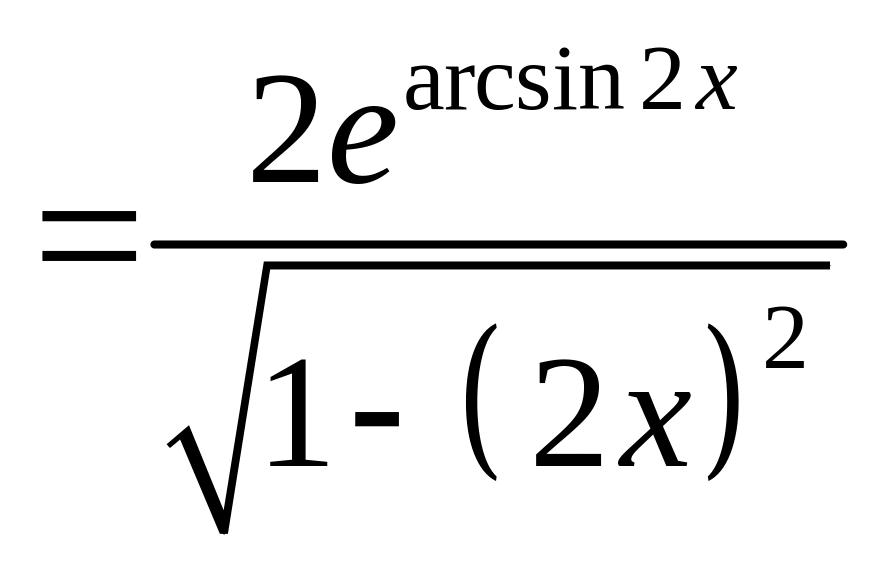Найдите производные следующих функций.

	.
	.
	.
	.
.	.
	. .
.	.
	.
.
.	.
.
.	.
	.
	.
	.
.	.
	.
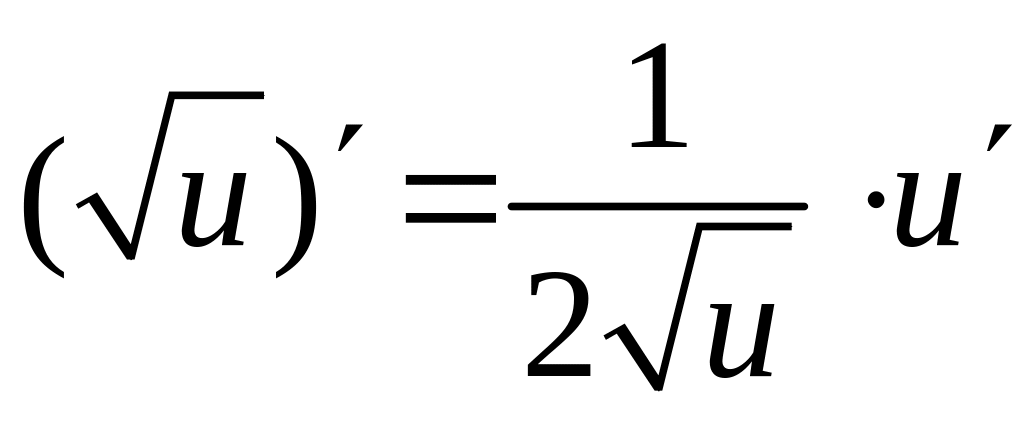
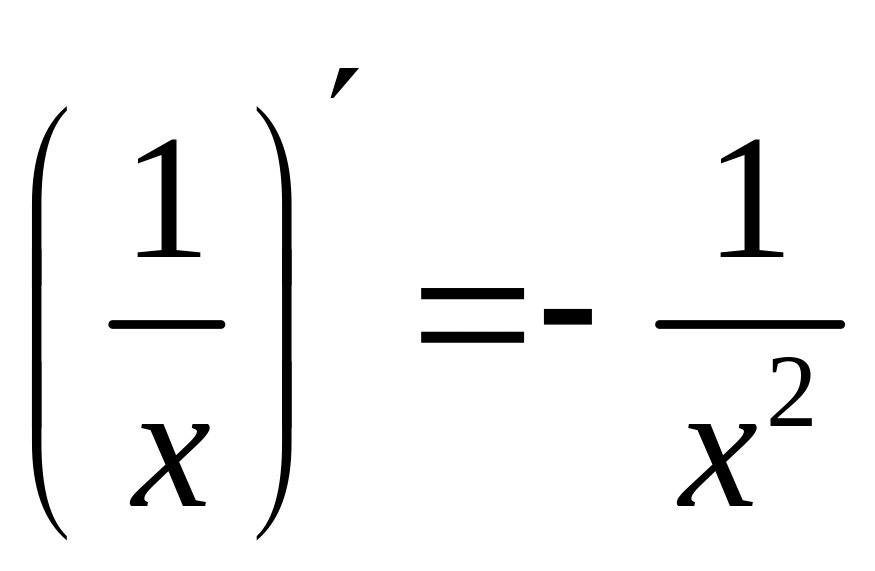
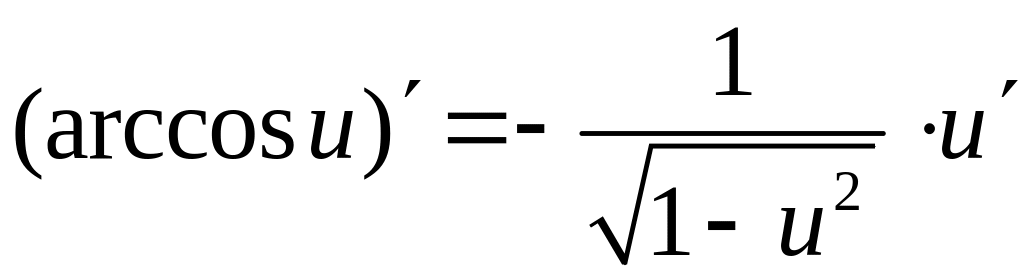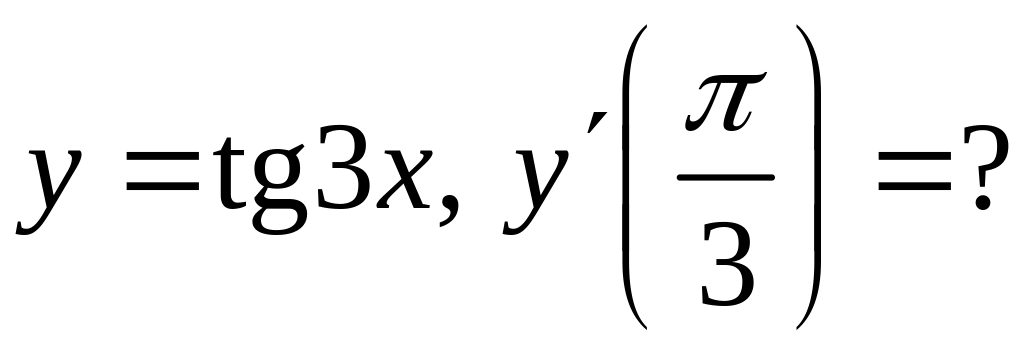