3. Показательная функция

Показательной функцией с основанием ( , ) называется функция, определенная на множестве всех действительных чисел и ставящая в соответствие числу число .

Областью определения показательной функции является множество , областью значений – интервал .

Основное свойство показательной функции: .

При показательная функция возрастает, и при стремящемся к ( ) тоже стремится к ( ). Этот факт записывают сл

е дующим образом Если же , то ( ). При показательная функция убывает, и при стремящемся к ( ) ( ); если же , то ( ).

Для обоих случаев ее график изображен на рис. 12, 13.

В математических исследованиях очень часто используют показательную функцию с основанием ; – иррациональное число: . Эта функция называется экспонентой и обозначается символом . Показательные функции с другими основаниями сводятся к экспоненте: .

4. Логарифмическая функция

П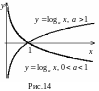 оказательная функция возрастает (убывает) при ( ) на всей области определения, поэтому существует обратная к ней функция, которую называют логарифмической функцией с основанием (или просто логарифмом). Обозначают логарифмическую функцию символом . Если , то вместо пишут (натуральный логарифм), если , то вместо пишут (десятичный логарифм).

Основные свойства логарифмической функции

1) область определения ;

2) множество значений ;

3) при логарифмическая функция возрастает и при , стремящемся к справа ( ), стремится к ( ), если же стремится к , то уходит на ( ). При функция убывает и , .

Графики логарифмической функции изображены на рис. 14.

4. Тригонометрические функции

В ыберем на плоскости прямоугольную декартову систему координат (рис. 15). Рассмотрим окружность единичного радиуса с центром в начале координат (единичную окружность). Пусть –произвольное действительное число: . Вектор с концом в точке повернем на угол радиан. В результате получится вектор . При повороте против часовой стрелки конец вектора опишет на единичной окружности дугу длины ( ), а при вращении в направлении часовой стрелки ( ) – длины .

Функция синус ставит в соответствие числу ординату такой точки М единичной окружности, для которой вектор образует с положительным направлением оси абсцисс угол в радиан.

Функция косинус ставит в соответствие числу абсциссу такой точки М единичной окружности, для которой вектор образует с положительным направлением оси абсцисс угол в радиан.

Итак, если точка имеет координаты , то есть , то

.

В тригонометрии используются также функции тангенс, котангенс, секанс и косеканс, определяемые соответственно равенствами:

, , и .

Свойства тригонометрических функций:

1) области определения , , ;

2) области значений , ;

3) косинус – четная функция, а синус, тангенс и котангенс – нечетные функции;

4) синус и косинус – функции периодические, с периодом , а тангенс и котангенс – функции периодические, с периодом ;

5

y

) синус возрастает на промежутках и убывает на промежутках , ;

косинус возрастает на промежутках и убывает на промежутках , .

Ф ункция возрастает на промежутках , ;

функция убывает на промежутках , ;

Г рафики тригонометрических функций изображены на рис. 16 – 19.

6) основные тождества, связывающие тригонометрические функции:

, , , ,

, ,

, .