3.4.3. Определенный интеграл
Определение
3. Определенным
интегралом от непрерывной на отрезке
функции
называется приращение какой-либо ее
первообразной
на этом отрезке:
.
Эта формула носит название формулы Ньютона-Лейбница.
Для обозначения приращения первообразной применяют также запись
.
Следует подчеркнуть, что в отличие от неопределенного интеграла, представляющего собой совокупность функций, определенный интеграл есть конкретное число, и это число не зависит от выбора первообразной, по которой оно считается.
Некоторые свойства определенного интеграла
1)
.
2)
.
3)
.
4)
.
5)
.
Вычисление определенных интегралов основано на применении формулы Ньютона-Лейбница. Для отыскания первообразной для подынтегральной функции применяются те же методы, что и при вычислении неопределенных интегралов.
1.
Интегрирование
по частям определенного интеграла
производится
по формуле
(4)
при
условии, что функции
и
имеют непрерывные производные на
.
2. Замена переменной в определенном интеграле использует формулу:
;
(5)
здесь предполагается, что функция
имеет непрерывную производную на отрезке
,
,
,
а функция
непрерывна в каждой точке
,
где
.
Задачи.
168.
Вычислить
.
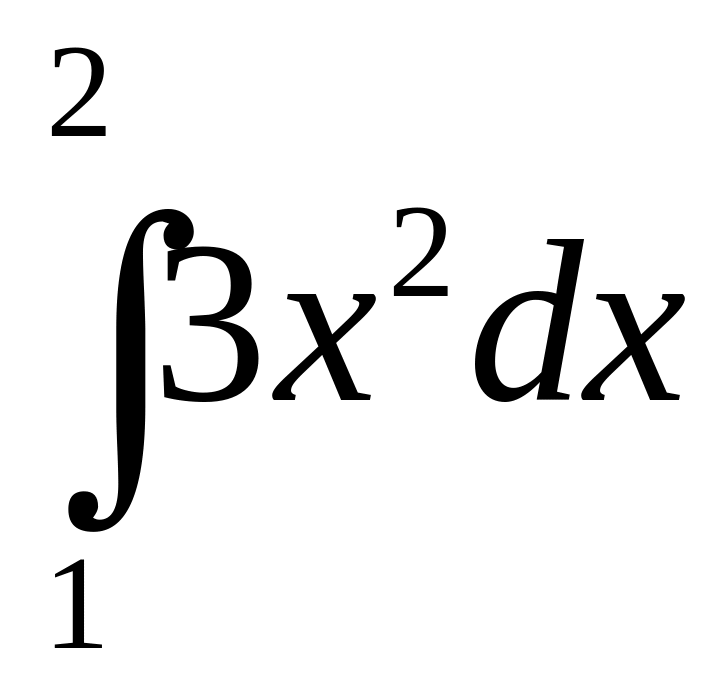Решение.
Так как
,
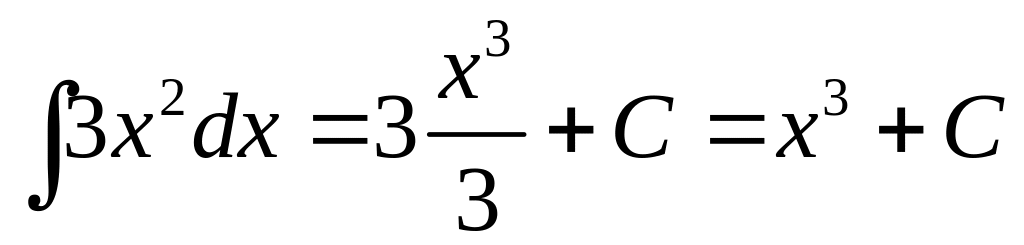то по формуле Ньютона – Лейбница
.
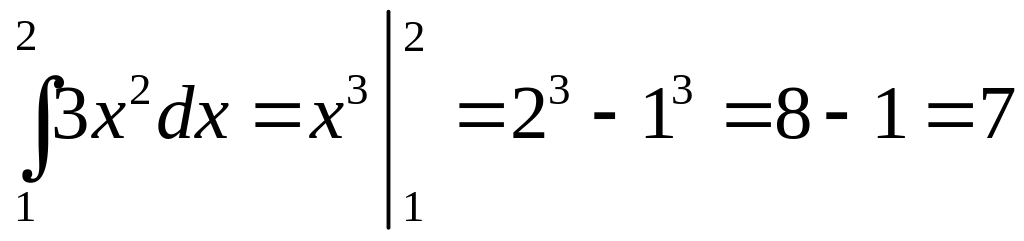169.
Вычислить
.
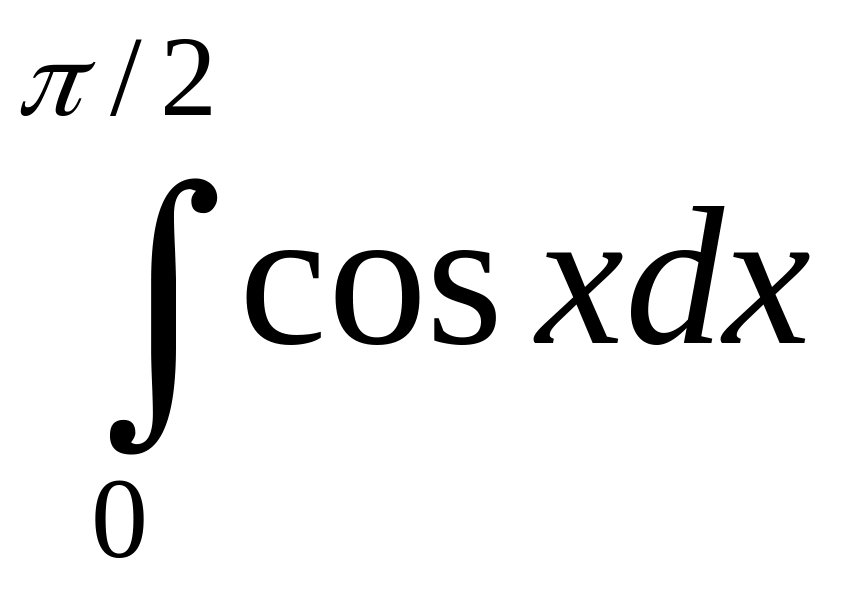Решение.
По формуле Ньютона-Лейбница и формуле
9 таблицы интегралов получаем:
.
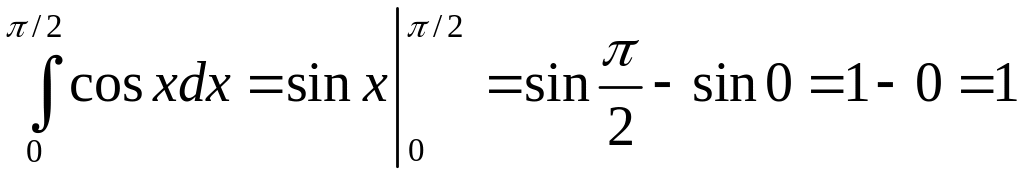170. Вычислить. .
Решение. Искомый неопределенный интеграл вычислен в упражнении 147. Поэтому
.
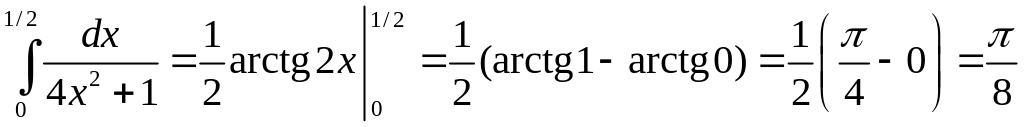171.
Вычислить.
.
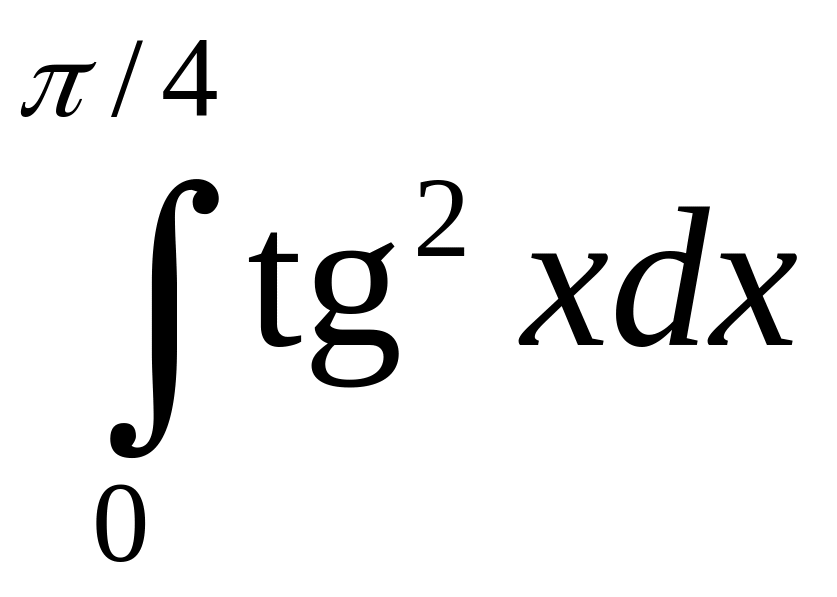Решение.
Из формулы
следует, что
.
Тогда искомый интеграл вычисляется
применением свойств интеграла и формулы
Ньютона–Лейбница.
.
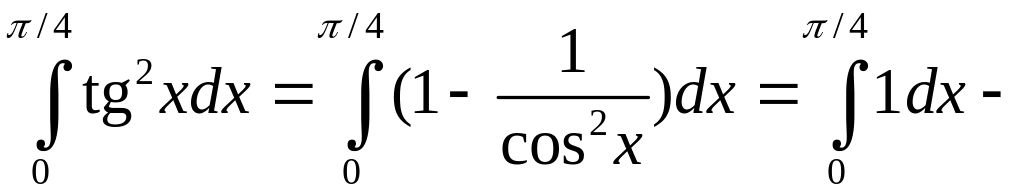
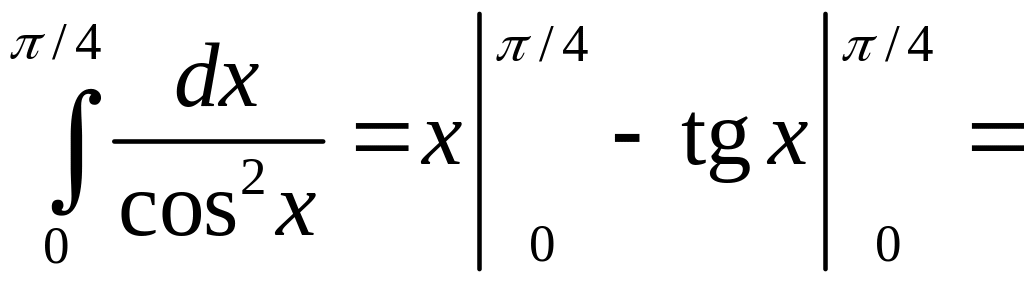
Вычислите определенные интегралы.
172.
|
173.
|
174.
|
175.
|
176.
|
177.
|
178.
|
179.
|
180.
|
181.
|
182.
|
183.
|
.
.
.
.
.
.
.
.
.
.
.
.
3.4. Некоторые приложения определенного интеграла
В данном параграфе рассмотрим некоторые задачи из сферы экономики и социологии, которые решаются с использованием интегралов. В этих задачах функция описывает какие-то явления или процессы производства либо социальной сферы.
1.
Пусть функция
описывает изменение производительности
некоторого производства с течением
времени. Тогда объем
продукции, произведенной за промежуток
времени
,
вычисляется по формуле:
(6)
184.
Изменение
производительности
производства
с течением времени от начала внедрения
нового технологического процесса
задается функцией
,
где
– время в месяцах. Найти объем продукции,
произведенной: а) за первый месяц, б)за
третий месяц, в) за шестой месяц, считая
от начала реконструкции производства.
Решение.
По формуле
(6):
=
.
Тогда
;
;
.
185.
Определите
объем выпуска продукции за первые пять
часов работы при производительности
,
где
– время в часах.
186.
При непрерывном
производстве химического волокна
производительность
(т/ч) растет с момента запуска 10 часов,
а затем остается постоянной. Сколько
волокна дает аппарат в первые сутки
запуска, если
при
.
2.
Пусть теперь
функция
характеризует неравномерность
распределения доходов среди населения,
– доля совокупного дохода, получаемого
долей
беднейшего населения. График этой
функции называется кривой
Лоренца
(Рис. 27) .
Очевидно, что
при
,
и неравномерность распределения доходов
тем больше, чем больше площадь фигуры
(рис.27). Поэтому в качестве меры указанной
неравномерности используют так
называемый
коэффициент
Джини
.
Этот коэффициент
равен
о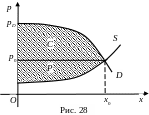
тношению
площади фигуры
к площади треугольника
.
1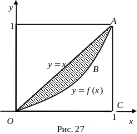
87.
По данным
исследований о распределении доходов
в одной из стран кривая Лоренца описывается
уравнением
,
.
Вычислить коэффициент Джини
.
Решение.
По формуле вычисления площади фигуры,
ограниченной линиями
и
,
,
получаем :
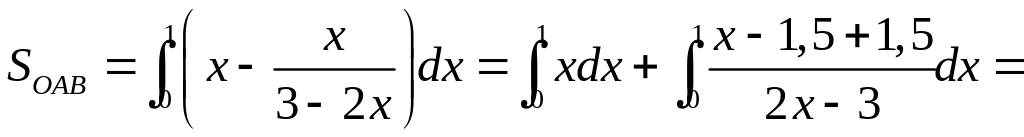
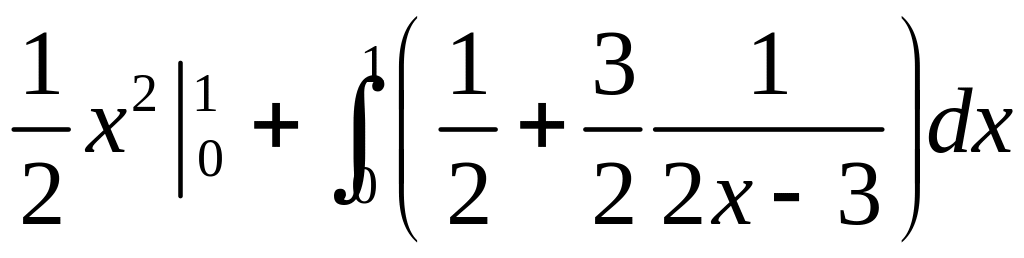
Тогда
.
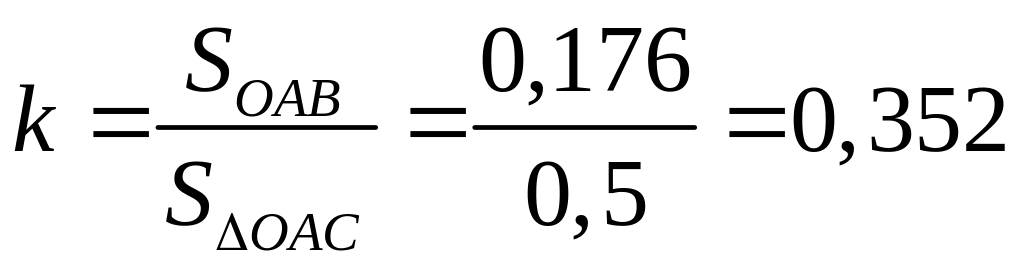188.
Кривые
Лоренца распределения дохода в некоторых
странах могут быть заданы уравнениями:
а)
б)
в)
1) Какую часть дохода получают 10% наиболее
низкооплачиваемого населения? Вычислить
коэффициент Джини для этих стран.
3.
Пусть
– функция спроса на некоторый товар
(ее график – кривая
),
– функция предложения (ее график –
кривая
),
– цена товара,
– величина спроса (предложения). Пусть
далее
– значение аргумента, при котором
значения функций спроса
и предложения
совпадают. Точка
называется точкой рыночного равновесия.
От реализации
единиц
товара по равновесной цене
доход будет равен произведению
.
Если предположить, что по мере
удовлетворения спроса цена непрерывно
снижается от максимальной
до равновесной
,
то доход составит
.
Таким
образом, если продавать товар по
равновесной цене
,
то потребителями сберегается величина
денежных средств, равная
Эта величина называется выигрышем
потребителя.
Аналогично, величина
называется выигрышем
поставщиков.
Величины
и
численно равны площадям соответствующих
криволинейных треугольников (рис. 28)
189.
Законы спроса
и предложения на рынке услуг имеют вид:
.
Найдите
выигрыши потребителей и поставщиков
в предположении
рыночного равновесия.
Решение.
Сначала
найдем точку
рыночного равновесия, для чего определим
значение
,
при котором
.
При этом условии
или
.
Отсюда получаем уравнение
.
Корни этого уравнения:
.
Так как величина спроса неотрицательна,
то
,
а значит,
.
Точка рыночного равновесия найдена:
(12, 42). Тогда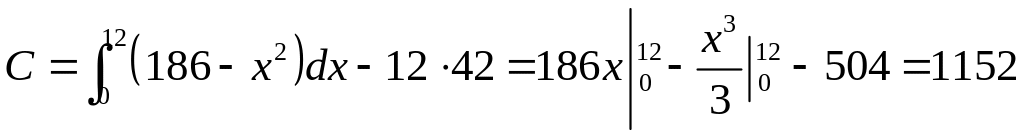 
,
.
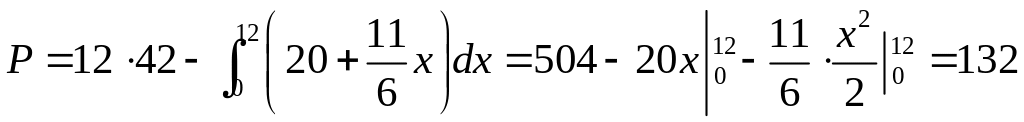190.
Уравнение спроса на некоторый товар
имеет вид
.
Найдите выигрыш потребителей, если
равновесная цена равна 70.
191.
Уравнение
спроса на некоторый товар имеет вид
.
Найдите выигрыш потребителей, если
равновесное количество товара равно10.
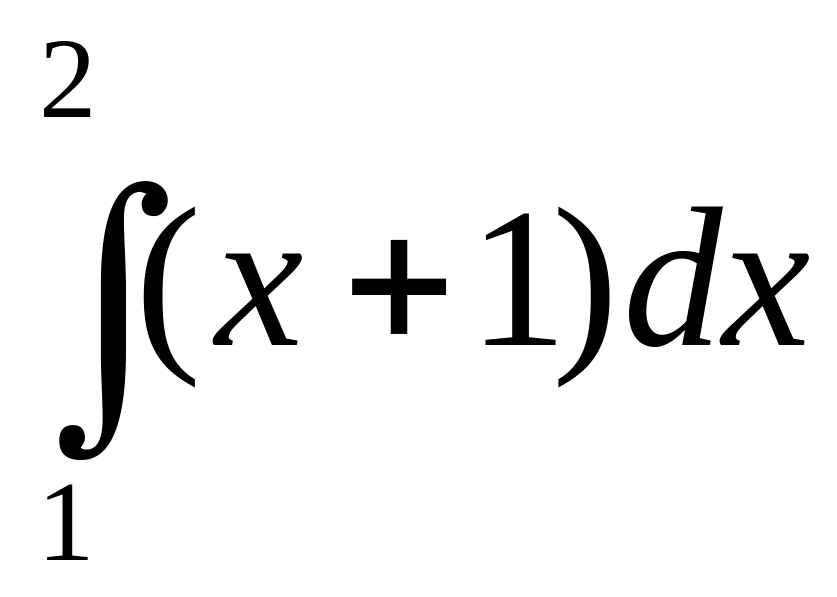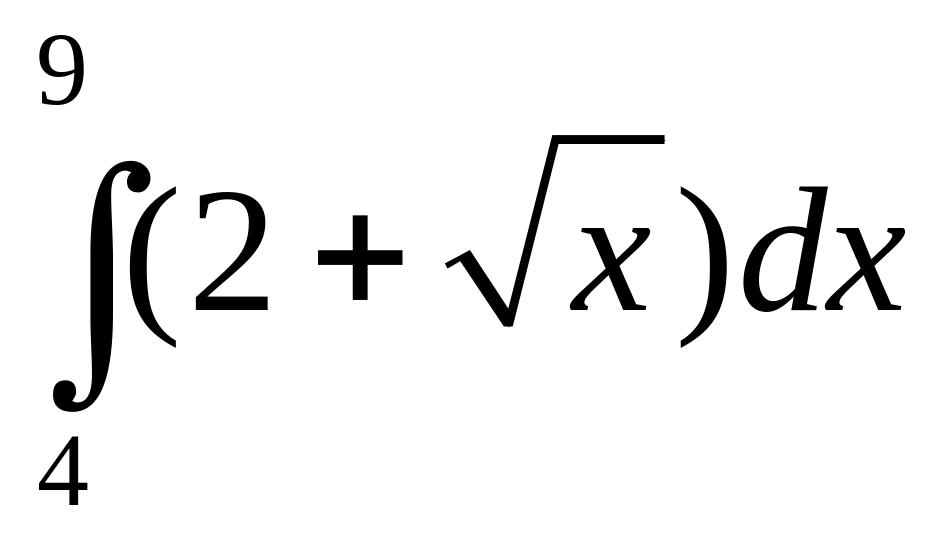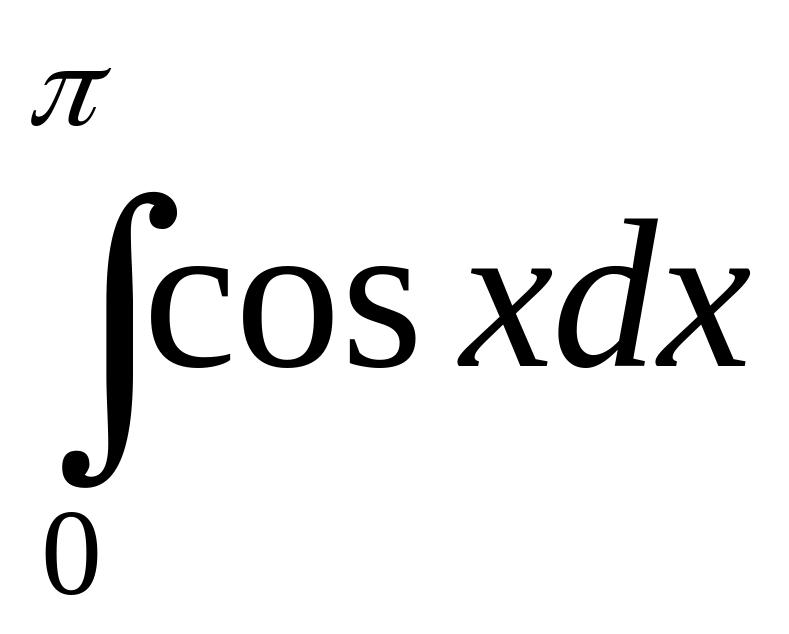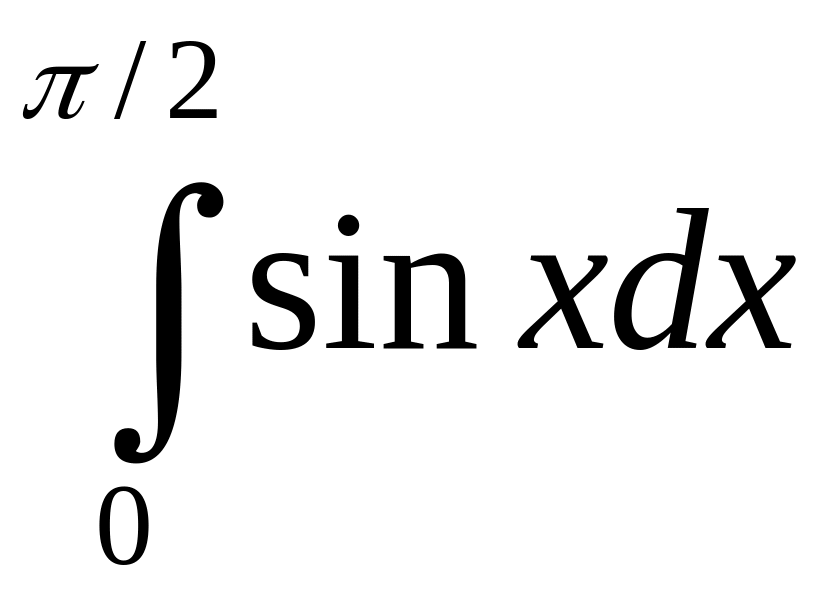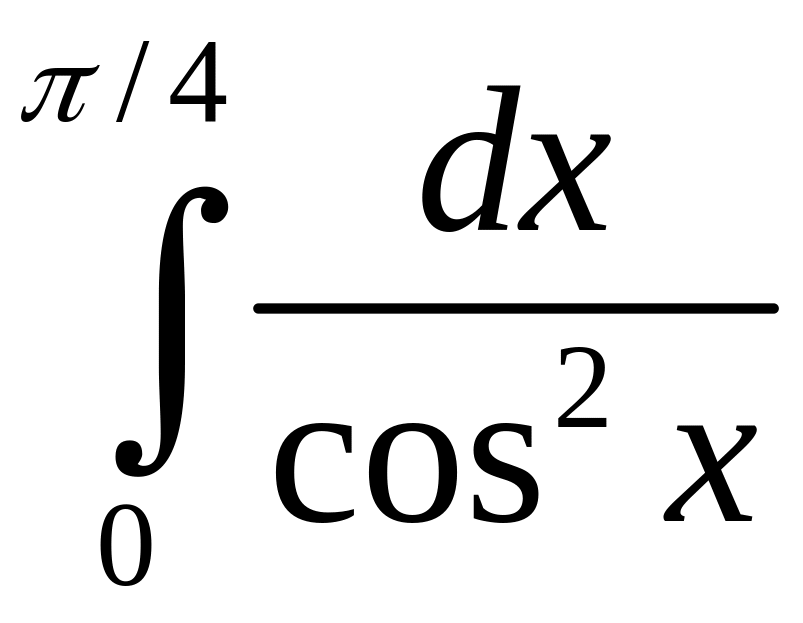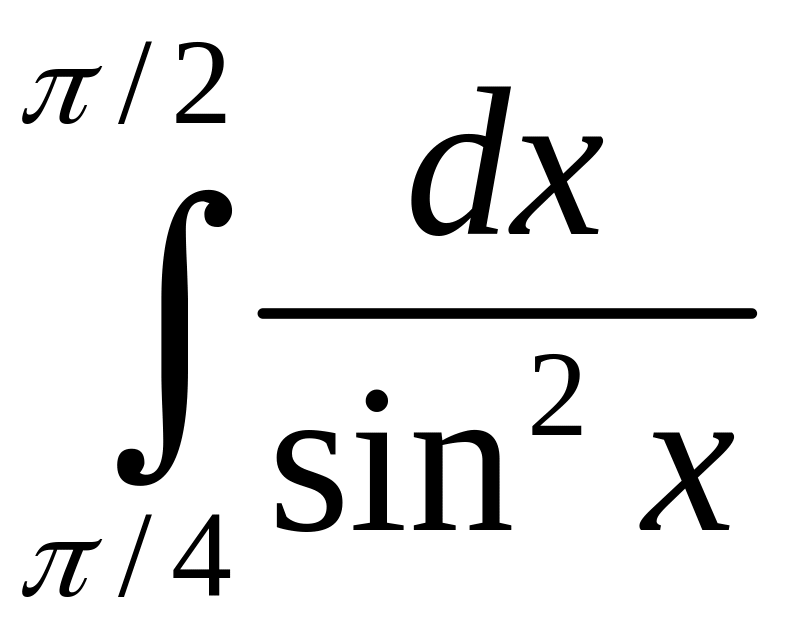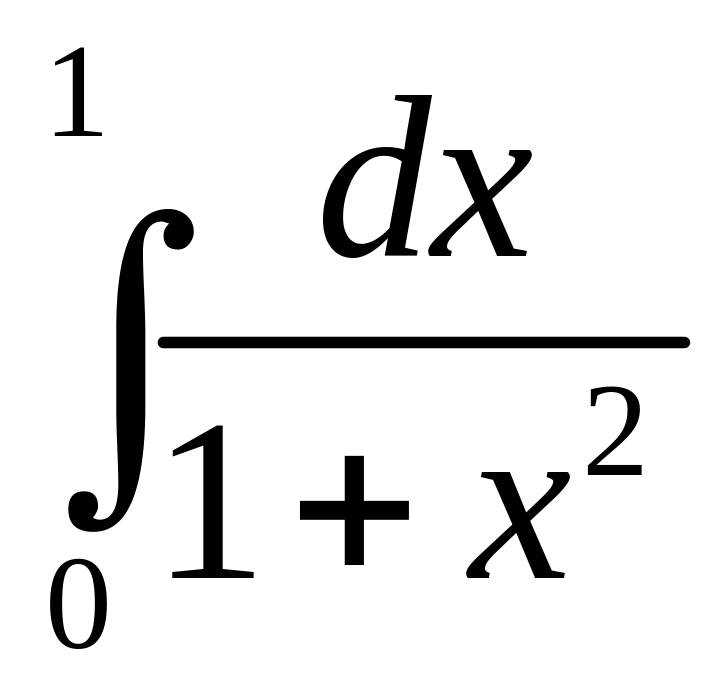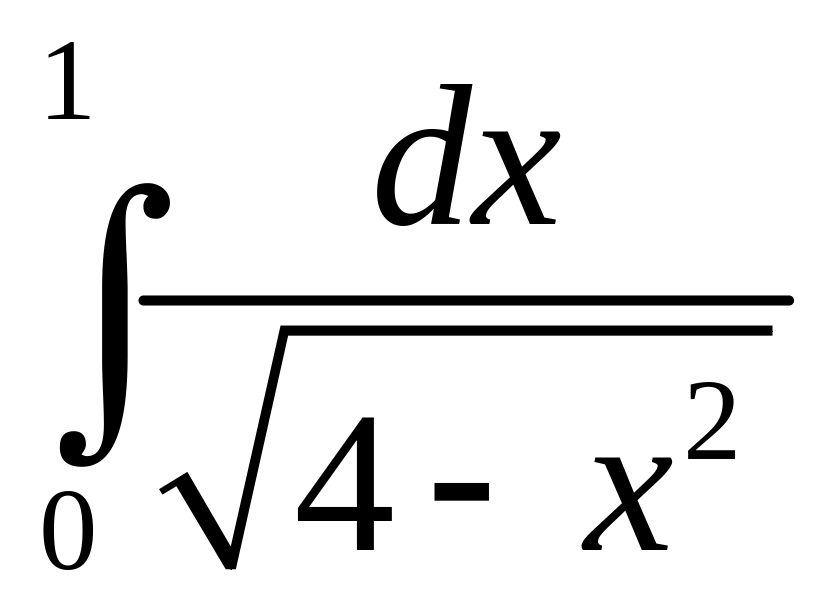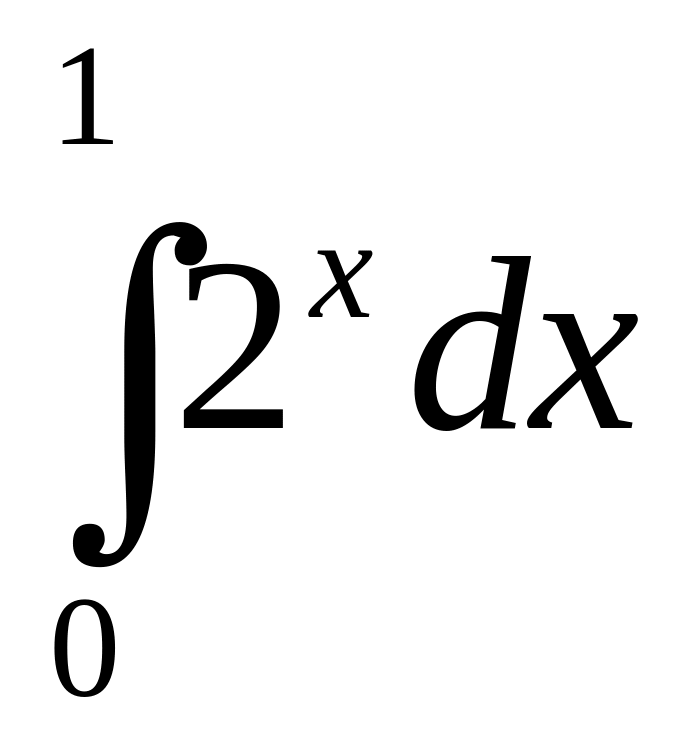