3. Элементы математического анализа
3.1. Функции. Элементарные функции
3.1.1. Понятие функции
Пусть
– некоторое множество действительных
чисел. Говорят, что на множестве
задана функция
,
если каждому числу
(аргументу
функции)
поставлено в соответствие единственное
число, обозначаемое символом
и называемое значением
функции в точке
x.
Множество
называется областью
определения функции и
обозначается символом
,
Множество всех значений
функции называется
областью значений функции
и обозначается символом
.
Итак,
Функцию , определенную на множестве , обозначают следующим образом:
,
или просто пишут
.
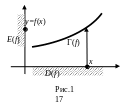
Графиком
функции f
(рис.1) называется множество всех точек
,
для которых
,
а
Наиболее
распространенным способом задания
функции является аналитический. Он
состоит в том, что задается формула, по
которой вычисляются значения функции
по значениям ее аргумента x.
При таком задании область определения
обычно не указывается, под ней понимается
множество всех тех значений x,
при которых данная формула имеет смысл.
Однако надо иметь в виду, что не всякая
формула задает функцию. В качестве
упражнения предлагаем выяснить, какие
из следующих формул определяют
как функцию от
:
,
,
.
Задачи.
Найдите область определения функций:
|
|
|
|
|
|
.
.
.
.
.
.Найдите область значений функций:
7.
|
8.
|
9.
|
10.
|
11. |
12.
|
13.
|
14.
|
15.
|
.
.
.
.
.
.
.
.
.
3.1.2. Основные виды функций
1. Четные, нечетные, общего вида.
Функция
называется
четной,
если для
любого значения
и выполняется условие
.
Функция
называется
нечетной,
если для
любого значения
и выполняется условие
.
Функция, которая не является четной и не является нечетной, называется функцией общего вида.
Можно
доказать, что график четной функции
симметричен относительно оси
,
а график нечетной функции симметричен
относительно начала координат.
Задачи.
Выясните четность (нечетность) функций:
16.
|
17. |
18.
|
19.
|
20. |
21. |
22.
|
23.
|
24.
|
.
.
.
.
.
.
.
.
.
2. Ограниченные и неограниченные
Функция
называется
ограниченной
на промежутке
,
если
существует такое число
,
что для всех
выполняется
неравенство
.
В противном случае функция называется
неограниченной.
Задачи
Выясните, какие функции являются ограниченными
25.
|
26. . |
27.
|
28. . |
29.
|
30.
|
.
.
.
.
3. Монотонные функции
Функция называется возрастающей на промежутке , если для любых двух значений аргумента из этого промежутка большему значению аргумента соответствует и большее значение функции.
В символической записи это определение выглядит следующим образом:
на
)
.
Функция называется убывающей на промежутке , если для любых двух значений аргумента из этого промежутка большему значению аргумента соответствует меньшее значение функции.
Символически это определение запишется следующим образом:
на
)
.
Возрастающие или убывающие на всей области определения функции называются монотонными.
Задачи
31.
Функции
и
возрастают на промежутке
.
Верно ли, что функции:
а)
и
возрастают на промежутке
;
б)
и
убывают на промежутке
?
4. Периодические функции
Функция
называется
периодической,
если
существует
такое число
,
что для любых
выполняются условия
и
.
Число
называется периодом функции.
Основные свойства периодических функций.
1)
Если
функция
периодическая и имеет период
,
то функция
,
где
постоянны, а
,
также периодическая, и ее период равен
.
2)
Если число
- период функции
,
то и число
,
где
,
тоже период этой функции.
Задачи
Найдите наименьший положительный период функции или докажите ее непериодичность:
32.
|
33.
|
34.
|
35. |
36. |
37.
|
.
.
.
.
.
.
38.
Докажите,
что число 2 не является периодом функции:
а)
;
б)
;
в)
;
г)
.
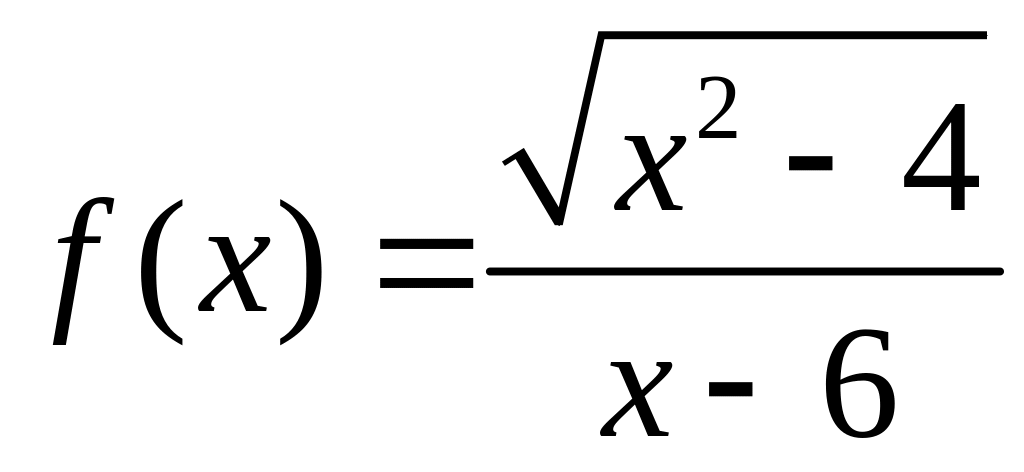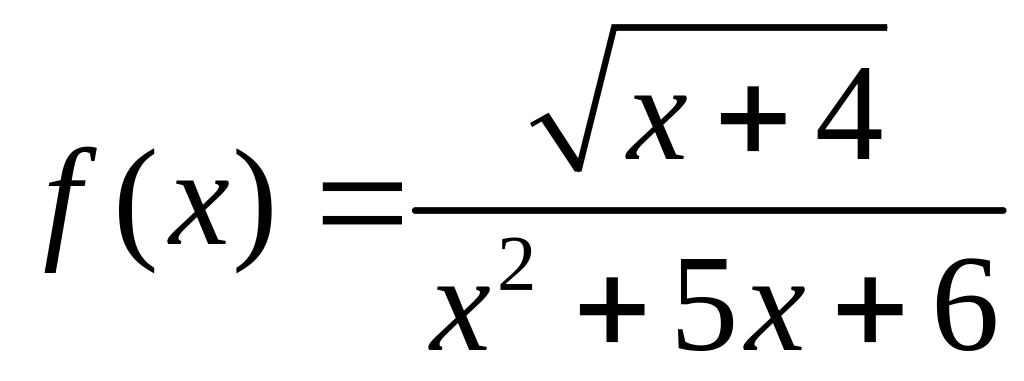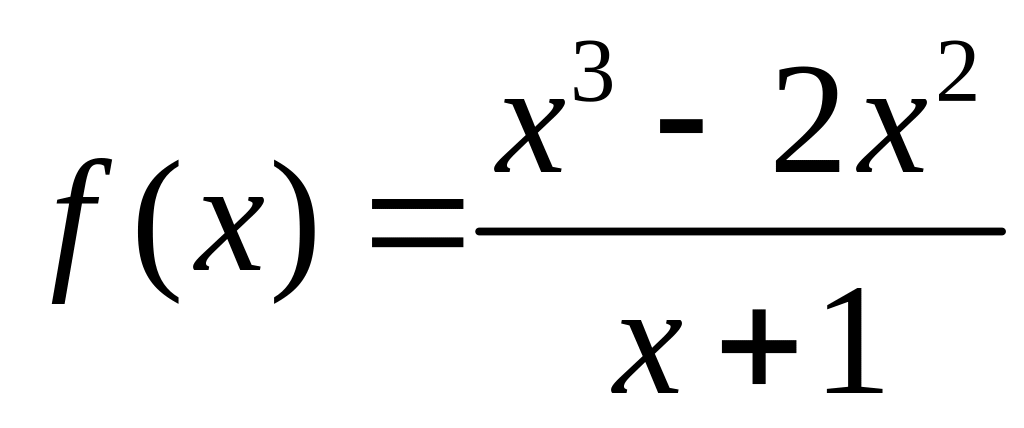