38.Аналітичні методи тестування гетероскедастичності. Тест Парка

Припустимо, що досліджується ПЛКРМ: 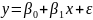. Припускається, що дисперсія є функцією і-го значення факторної ознаки x. Парк запропонував таку функціональну залежність: 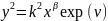, де - деякі невідомі параметри, 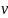-випадкова величина. Аби оцінити невідомі параметри останню модель необхідно лінеаризувати: .

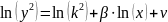Для практичного застосування замість величини беруть квадрат в.в

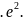
Алгоритм проведення тесту Парка:

1.Будуємо вибіркову ПЛКРМ: .

2.Знаходимо випадкові відхилення , .

3.Для кожного спостереження визначаємо

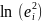
4.Будуємо кореляційно-регресійну модель 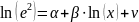, де =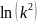 Замінимо: 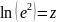; . Тепер можна застосувати метод найменших квадратів для оцінення параметрів.

5.Перевіряємо статистичну значущість коефіцієнта на підставі t-статистики за формулою: 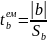. Якщо коефіцієнт статистично значущий, то це означає, що між та є зв'язок, тобто у вибірковій сукупності наявна гетероскедастичність, в іншому випадку навпаки.

39.Аналітичні методи тестування гетероскедастичності. Тест Глейзера

Він є розширенням тесту Парка і доповнює його аналізом інших видів залежності між дисперсіями випадкових відхилень 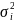і значеннями факторної ознаки . Згідно з цим методом оцінюють кореляційно-регресійну модель залежності абсолютних значень відхилень , які тісно пов’язані з , від . При цьому таку залежність моделюють за допомогою такої кореляційно-регресійної моделі в загальному випадку: 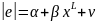. Замінюючи L , можна побудувати різні кореляційно-регресійні моделі. Здебільшого беруть L = -1;-0,5; 0,5; 1;…. Оскільки фактична форма залежності невідома, то можна підбирати різні види залежності, зокрема: ;

; ; ;

; ; .

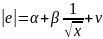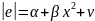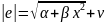Про наявність гетероскедастичності свідчить статистична значущість параметрів , а також високий коефіцієнт кореляції між змінними моделі. Статистична значущість параметрів визначається шляхом перевірки нульових гіпотез:

-вільний член ; -коефіцієнт регресії .

Перевірка цих гіпотез здійснюється за допомогою t-статистики Стьюдента. Якщо для декількох моделей є статистично значущим, то обирають модель на підставі перевірки їхніх коефіцієнтів кореляції та середньоквадратичних відхилень параметрів, і при цьому можливі наступні випадки:

- ;

- .

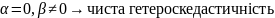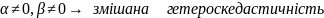Переваги цього тесту: інформація про характер гетероскедастичності.

40. Аналітичні методи тестування гетероскедастичності. Тест Годфрея

Тест Годфрея передбачає побудову допоміжних кореляційно-регресійних моделей використовуючи квадрати відхилень , тобто кореляційно-регресійних залежностей виду 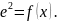При цьому в загальному прикладі таку залежність моделюють: 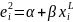+ . Змінюючи значення L будуємо наступні кореляційно-регресійні моделі:

;

;

;

;

;

+ ;

+ ;

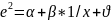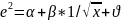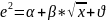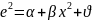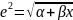Про наявність гетероскедастичності свідчить статистична значущість параметрів , а також високий коефіцієнт кореляції між змінними моделі. Статистичну значущість параметрів моделі визначають шляхом перевіряння нульових гіпотез:

• Вільний член моделі

• Коефіцієнт регресії

Перевіряння нульових гіпотез здійснюють за допомогою 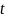-статистики Стьюдента. Якщо для декількох кореляційно-регресійних моделей коефіцієнт регресії є статистично значущим, то ”найкращу” з цих моделей вибирають на підставі порівняння їхніх коефіцієнтів кореляції та середньоквадратичних відхилень параметрів .

У разі, коли та 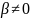, явище називають чистою гетероскедастичністю, а коли та , то наявна змішана гетероскедастичність.