
- •1.Основні припущення класичного кореляційно-регресійного аналізу та висновки з них.
- •2.Поняття симультативно модел . Скорочена форма симульт моделі та способи запису.
- •3. Поняття застосування симультативних моделей. Модель попиту на товар.
- •4. Поняття застосування симультативних моделей. Модель грошової пропозиції.
- •5. Поняття застосування симультативних моделей. Модель рівноваги на ринку товарів.
- •6. Поняття застосування симультативних моделей. Модель рівноваги на ринку грошей.
- •7. Проблема ототожнення в см. Умова порядку та рангова умова ототожнення
- •8. Недоліки застосування класичного методу найменших квадратів до побудови см. Загальний огляд методів оцінювання параметрів см.
- •Метод непрямих найменших квадратів;
- •Двокроковий метод найменших квадратів;
- •9. Рекурсивні симультативні моделі та методи їх оцінювання.
- •10. Поняття дистрибутивно-лагової моделі . Причини і види лагів.
- •11. Поняття авторегресійної моделі та методи оцінювання параметрів
- •12. Суть, причини та наслідки автокореляції
- •13. Тестування автокореляції. Графічний метод.
- •14.Визначення на основі статистики Дарбіна-Уотсона
- •15.Метод Хілдрета-Лу
- •17. Суть та наслідки гетероскедастичності
- •18. Тестування гетероскедастичності. Графічний аналіз випадкових відхилень.
- •19. Суть та наслідки мультиколінеарності
- •20. Тестування наявності мультиколінеарності
- •21. Визначення рівня мультиколінеарності
- •22. Методи усунення мультиколінеарності
- •23. Метод непрямих найменших квадратів
- •24. Двокроковий метод найменших квадратів
- •25. Послідовне оцінювання параметрів дистрибутивно-лагових моделей
- •26. Модель Койка
- •27. Модель адаптивних очікувань (перша модель модифікації Койка)
- •28. Модель часткових пристусувань(друга модифікації моделі Койка)
- •29. Підхід Альмона до оцінювання параметрів дистрибутивно-лагових моделей
- •30. Тестування автокореляції. Метод рядів
- •31. Методи усунення автокореляції
- •32. Тестування автокореляції. Критерій Дарбіна-Уотсона (dw-критерій)
- •33. Тестування автокореляції. H-критерій Дарбіна-Уотсона
- •34. Метод Кохрана-Оркатта
- •35. Аналітичні методи тестування гетероскедастичності. Критерій Бартлетта
- •36. Аналітичні методи тестування гетероскедастичності. Тест рангової кореляції Спірмена
- •37.Аналітичні методи тестування гетероскедастичності. Тест Голдфельда-Квандта
- •38.Аналітичні методи тестування гетероскедастичності. Тест Парка
- •39.Аналітичні методи тестування гетероскедастичності. Тест Глейзера
- •40. Аналітичні методи тестування гетероскедастичності. Тест Годфрея
- •41. Метод зважених найменших квадратів (дисперсії випадкових величин відомі)
- •42.Метод зважених найменших квадратів (дисперсії відхилень невідомі)
- •43. Алгоритм Феррара — Глобера.
- •44. Узагальнений метод найменших квадратів (матричний підхід)
20. Тестування наявності мультиколінеарності
Єдиного методу визначення мультиколінеарності немає. На практиці використовують такі методи тестування наявності мультиколінеарності:
Оцінювання значення коефіцієнта множинної детермінації і статистичної незначущості параметрів моделі
Одночасна наявність високого значення високого значення коефіцієнта множинної детермінації та статистичної незначущості деяких коефіцієнтів множинної регресії є ’класичною’ ознакою мультиколінеарності.
Аналіз значень парних коефіцієнтів кореляції для факторних ознак
Якщо значення хоча б одного коефіцієнта парної кореляції більше за 0,8, то мультиколінеарність є серйозною проблемою. Значення парних коефіцієнтів кореляції дає кореляційна матриця:
 де
де
 коефіцієнт кореляції між факторним
ознаками
та
коефіцієнт кореляції між факторним
ознаками
та
 .
.
Недоліком
цього тесту є те, що високі значення
парних коефіцієнтів кореляції -
достатня, але не необхідна умова наявності
мультиколінеарності. Під час побудови
множинної кореляційно-регресійної
моделі мультиколінеарність може бути
і при відносно невеликих значеннях
парних коефіцієнтів кореляції. У цьому
разі знаходять визначник кореляційної
матриці, який набуває значення від 0 до
1.Можна виділити 3 випадки:1.Якщо
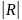 =0,
то наявна повна мультиколінеарність;2.Якщо
=0,
то наявна повна мультиколінеарність;2.Якщо
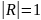 ,
то мультиколінеарність відсутня;3. Що
ближче
до
нуля, то впевненіше можна стверджувати,
що мультиколінеарність наявна.
,
то мультиколінеарність відсутня;3. Що
ближче
до
нуля, то впевненіше можна стверджувати,
що мультиколінеарність наявна.
Аналіз значень часткових коефіцієнтів кореляції
Частковий коефіцієнт кореляції для факторних ознак характеризує тісноту зв’язку між 2ма факторними ознаками за умови , що всі інші факторні ознаки не впливають на цей зв'язок.
Оцінювання відношення власних значень та умовного індексу
Знаходимо
власні значення матриці
 та розраховуємо відношення
та розраховуємо відношення
 ;
де
;
де
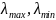 -
відповідно максимальне і мінімальні
власні значення матриці
.
Якщо
-
відповідно максимальне і мінімальні
власні значення матриці
.
Якщо
 то
мультиколінеарність відсутня; Якщо
то
мультиколінеарність відсутня; Якщо
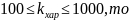 мультиколінеарність
помірна;
мультиколінеарність
помірна;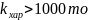 мультиколінеарність
висока. Умовним індексом
мультиколінеарність
висока. Умовним індексом
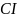 назв. арифметичне значення квадратного
кореня з відношення
назв. арифметичне значення квадратного
кореня з відношення
 :
:
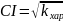 .
Якщо
.
Якщо
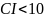 то мультиколінеарність відсутня; Якщо
то мультиколінеарність відсутня; Якщо
 мультиколінеарність
помірна;
мультиколінеарність
помірна;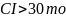 мультиколінеарність
висока.
мультиколінеарність
висока.
Алгоритм Феррара-Глобера
Крок
1: Нормалізуємо факторні ознаки:
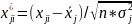 де
де
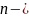 величина
вибірки,
величина
вибірки, -
середнє значення j-ї
факторної ознаки,
-
середнє значення j-ї
факторної ознаки,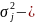 дисперсія
j-ї факторної ознаки. Крок
2: Обчистення кореляційної матриці
R:
дисперсія
j-ї факторної ознаки. Крок
2: Обчистення кореляційної матриці
R:
 ,
де
,
де
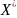 -
матриця нормалізованих значень фак..озн.
Крок 3:Обчислення значення
-
матриця нормалізованих значень фак..озн.
Крок 3:Обчислення значення
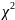 критерію-
критерію-
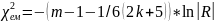 ,
,
де
-
визначник кореляційної матриці. Знаходимо
табличне
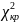 при
при
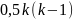 ступенях вільності і рівні значущості
ступенях вільності і рівні значущості
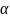 .
Якщо
.
Якщо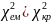 ,
мультикол.наявна, якщо
,
мультикол.наявна, якщо
 мультикол.відсутня. Крок 4:Визначення
матриці помилок С:
мультикол.відсутня. Крок 4:Визначення
матриці помилок С:
 .
Крок 5: Розрахунок значень F-критерію:
.
Крок 5: Розрахунок значень F-критерію:
 ,
де
,
де – діагональні елементи матриці С.
Знаходимо табличне
– діагональні елементи матриці С.
Знаходимо табличне
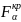 при
при
 і
і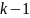 ступенях вільності і рівні значущості
.
Якщо
ступенях вільності і рівні значущості
.
Якщо
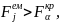 то
j-та факторна ознака
колінеарна і потрібно вилучити її з
переліку змінних моделі. Якщо
то
j-та факторна ознака
колінеарна і потрібно вилучити її з
переліку змінних моделі. Якщо
 то
j-та факторна ознака не
колінеарна. Крок 6:Обчислення
часткових коефіцієнтів кореляції
то
j-та факторна ознака не
колінеарна. Крок 6:Обчислення
часткових коефіцієнтів кореляції
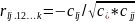 ,
де с- елементи матриці С.Крок 7:
Розрахунок значень t-критерію:
,
де с- елементи матриці С.Крок 7:
Розрахунок значень t-критерію:
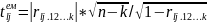 .
Знаходимо табличне
.
Знаходимо табличне
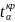 при
ступенях вільності і рівні значущості
.
Якщо
при
ступенях вільності і рівні значущості
.
Якщо
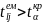 ,
то між факторними ознаками
,
то між факторними ознаками
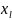 i
наявна колінеарність.Якщо
i
наявна колінеарність.Якщо
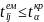 ,
то факторні ознаки
i
не колінеарні.
,
то факторні ознаки
i
не колінеарні.
