1.Основні припущення класичного кореляційно-регресійного аналізу та висновки з них.

2.Поняття симультативно модел . Скорочена форма симульт моделі та способи запису.

3.Поняття застосування симультативних моделей. Модель попиту на товар.

4.Поняття застосування симультативних моделей. Модель грошової пропозиції.

5.Поняття застосування симультативних моделей. Модель рівноваги на ринку товарів.

6.Поняття застосування симультативних моделей. Модель рівноваги на ринку грошей.

7.Проблема ототожнення в СМ. Умова порядку та рангова умова ототожнення

8.Недоліки застосування класичного методу найменших квадратів до побудови СМ. Загальний огляд методів оцінювання параметрів СМ.

9.Рекурсивні симультативні моделі та методи їх оцінювання.

10.Поняття дистрибутивно-лагової моделі . Причини і види лагів.

11.Поняття авторегресійної моделі та методи оцінювання параметрів

12.Суть, причини та наслідки автокореляції

13.Тестування автокореляції. Графічний метод.

14.Визначення  на основі статистики Дарбіна-Уотсона

15.Метод Хілдрета-Лу

16.Метод перших різниць

17.Суть та наслідки гетероскедастичності

18.Тестування гетероскедастичності. Графічний аналіз випадкових відхилень.

19.Суть та наслідки мультиколінеарності

20.Тестування наявності мультиколінеарності

21.Визначення рівня мультиколінеарності

22.Методи усунення мультиколінеарності

23.Метод непрямих найменших квадратів

24.Двокроковий метод найменших квадратів

25.Послідовне оцінювання параметрів дистрибутивно-лагових моделей

26.Модель Койка

27.Модель адаптивних очікувань (перша модель модифікації Койка)

28.Модель часткових пристусувань(друга МОДИФІКАЦІЇ моделі Койка)

29.Підхід Альмона до оцінювання параметрів дистрибутивно-лагових моделей

30.Тестування автокореляції. Метод рядів

31.Методи усунення автокореляції

32.Тестування автокореляції. Критерій Дарбіна-Уотсона (DW-критерій)

33.Тестування автокореляції. h-критерій Дарбіна-Уотсона

34.Метод Кохрана-Оркатта

35.Аналітичні методи тестування гетероскедастичності. Критерій Бартлетта

36.Аналітичні методи тестування гетероскедастичності. Тест рангової кореляції Спірмена

37.Аналітичні методи тестування гетероскедастичності. Тест Голдфельда-Квандта

38.Аналітичні методи тестування гетероскедастичності. Тест Парка

39.Аналітичні методи тестування гетероскедастичності. Тест Глейзера

40.Аналітичні методи тестування гетероскедастичності. Тест Годфрея

41.Метод зважених найменших квадратів (дисперсії випадкових величин відомі)

42.Метод зважених найменших квадратів (дисперсії відхилень невідомі)

43.Алгоритм Феррара — Глобера.

44.Узагальнений метод найменших квадратів (матричний підхід)

1.Основні припущення класичного кореляційно-регресійного аналізу та висновки з них.

1.Математичне сподівання випадкової величини дорівнює нулю. . 2.Відсутність автокореляції між випадковими величинами : . Припущення

означає, що випадкові величини незалежні одна від одної.

3. Гомоскедастичність: .

4. Незалежність між значеннями випадкової величини і значеннями незалежної змінної x: .

5. Випадкова величини розподілена нормально з математичним сподіванням 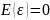та дисперсією .

6. Регресійну модель специфіковано правильно (вибрано правильну функціональну форму моделі). Економетричне дослідження містить етап специфікації математичної моделі, що має бути адекватною економічному об’єкту, процесу, явищу, яке вивчають. При специфікації моделі потрібно відповісти на такі запитання: які змінні потрібно включити в модель, якою повинна бути функціональна форма моделі, які можливі припущення щодо змінних можна зробити в моделі.

2.Поняття симультативно модел . Скорочена форма симульт моделі та способи запису.

Симультативною моделлю (системою одночасних рівнянь) називають систему рівнянь, яка описує взаємну залежність між ендогенними та екзогенними змінними.

Структурна економетрична модель— це система рівнянь, яка описує структуру взаємозв'язків між економічними змінними.

y_i=f_i(A,X,ε), i=1,m

φ_s(A,X,Y,ε)=o, s=1,p

y_i=ψ_i(A,X,Y,ε), i=1,m

Структурні рівняння виражають одні ендогенні змінні як функції інших ендогенних змінних та попередньо визначених екзогенних змінних і випад­кових величин.

Під час побудови симультативної моделі екзогенні змінні будемо познача­ти через x_j j=1,k ендогенні змінні — через y_i i=1,m ; параметри, які стоять біля екзогенних змінних, — через γ_ij (або a_ij ) параметри, що стоять біля ен­догенних змінних, — через β_ij (або b_ij ) вільні члени рівнянь — через β_i0 (або a_i0). Тоді симультативна модель матиме вигляд:

y₁ = β₁₀ +β₁₁y_i +…+β_1jy_i+γ₁₁x_ij+…+γ_1jx_ij + ε₁

…………………………………………

yi = β_i0 +β_i1y_i +…+β_ijy_i+γ_i1x_ij+…+γ_ijx_ij + ε_i

Якщо всі рівняння звести до вигляду, коли зліва всі ендогенні та екзогенні змінні, а зправа вільні члени та не пояснений вплив, то запис симультативної моледі можна предсавти у вигляді таблиці, де на перехресті рядків і стовпців будуть виставлятись коефіцієнти що відповідають цій змінній у даному рівнянні.

	y1	y2	…	yn	x1	x2	…	xn
1
2
…
s

Скороченою (зведеною) формою симультативної моделі назива­ють модель, у якій ендогенні змінні виражені як функції лише екзогенних змінних та випадкових величин.

Скорочену форму симультативної моделі можна записувати двома спосо­бами: згорнутим вираженням і розгорнутим вираженням. Згорнуте вираження: y_it = π_i0+ π_i1x_1t+ π_i2x_2t+…+ π_ikx_1k+ν_it , деπ_ij, і = 1,т, j=0,k — невідомі параметри згорнутого вираження скороченої форми моделі.

Розгорнуте вираження: y_it =λ_i0( β,γ)+ λ_i1( β,γ)x_1t+ λ_i2( β,γ)x_2t+…+ λ_ik( β,γ)x_1k+ν_it( β,γ,ε), де λ_ii (β,γ)представлення параметрів скороченої форми через струк­турні параметри.

У згорнутому вираженні ендогенні змінні представлені як функції лише екзогенних змінних з невідомими параметрами та випадкових величин, у роз­горнутому вираженні ендогенні змінні представлені як функції екзогенних змінних, структурних параметрів та випадкових величин. Систему рівнянь, яка описує зв'язок між параметрами згорнутого та розгорнутого вираження скороченої форми симультативної моделі.

π_i0 = λ_i0( β,γ), π_i1= λ_i1( β,γ), …, π_ij= λ_ij( β,γ), називають системою параметричних взаємозвязків

На практиці у розгорнутому записі скороченої форми си­мультативної моделі дуже часто замість структурних параметрів β, γ викори­стовують параметри α, β вихідної моделі й не перепозначають змінні.