8. Общая теория цилиндрических проекций. Уравнения цилиндрических проекций.

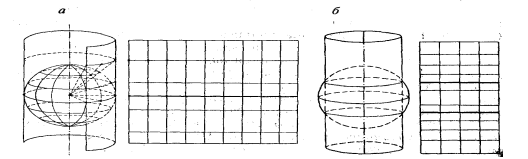
Нормальная сетка цилиндрических проекций имеет простой вид: все меридианы — параллельные прямые, расположенные на одинаковом расстоянии друг от друга, параллели — прямые, перпендикулярные к меридианам; расстояния между ними изменяются в зависимости от свойств проекции. Прямоугольные координаты этих проекций: х = f(ф); у = βλ , где параметр проекции β = const. За ось X выбирают один из меридианов, за ось Y — экватор или одну из параллелей.Функцию, определяющую абсциссу проекции, находят под условием равноугольности, равновеликости или равнопромежуточности изображения; соответственно и цилиндрические проекции могут быть равноугольными, равновеликими или равнопромежуточными по меридианам. Кроме перечисленных проекций в кар-тографической практике встречаются также произвольные по характеру искажений проекции (с заданным распределением искажений и перспективно-цилиндрические проекции, получаемые геометрическим путем).

Картографируемую поверхность принимают в этих проекциях за эллипсоид или за сферу. Главные направления в нормальных цилиндрических проекциях совпадают с меридианами и параллелями, поэтому масштабы по меридианам и параллелям являются экстремальными.

Общие формулы нормальных цилиндрических проекций эллипсоида:

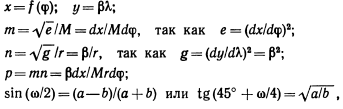где а и b— экстремальные масштабы длин; β = const. При получении параметра β ставят условие, чтобы главный масштаб сохранялся на параллелях с широтой ± : откуда β= , где - радиусы главных параллелей. Если = 0°, то β= а, где а — большая полуось эллипсоида.

Искажения в нормальных цилиндрических проекциях являются функцией только широты, поэтому изоколы совпадают с параллелями и имеют вид прямых. Нормальные цилиндрические проекции целесообразно применять при создании карт на территории, вытянутые вдоль географического экватора.

По характеру искажений цилиндрические проекции содержат весь спектр проекций.

Равновеликую цилиндрическую проекцию в 1772 г. разработал И.Г.Ламберт. Эратосфеном была составлена карта мира с сеткой меридианов и параллелей в виде взаимно перпендикулярных равноотстоящих прямых. Вероятно, это была равнопромежуточная цилиндрическая проекция. В 1569 г. знаменитый фламандский картограф Меркатор в равноугольной цилиндрической проекции создал первую многолистную карту мира, предназначенную для использования в навигации. Впоследствии проекция стала называться его именем и получила широкое распространение в мореплавании благодаря весьма ценному ее свойству — в проекции Меркатора линия постоянного азимута (локсодромия) изображается прямой.

--------------------------------------------------------------------------------------------------------

9. Прямые способы построения картографических проекций. Вид картографической сетки поликонической проекции.

Картографические проекции получают, решая прямую или обратную задачу математической картографии.. К прямым способам относятся те, которые основаны на решении прямой задачи математической картографии. В прямой задаче математической картографии вначале тем или иным путем задается проекция (а именно, способом ее построения, эскизом картографической сет-

ки, уравнениями и др.), а затем в результате ее изучения получают различные показатели, характеризующие искажения и свойства этой проекции.

Для получения проекций чаще всего применяют:

1) способы графических построений;

2) способы перспективного проектирования шара (реже эллипсоида): • на плоскость; • на поверхность цилиндра, впоследствии развертываемую в плоскость; • на поверхность конуса, также впоследствии развертываемую в плоскость;

3) способы построения проекций обработкой их эскизов;

4) разные способы видоизменения и преобразования уже известных проекций, в результате чего получают так называемые производные проекции.

Подавляющее большинство проекций получено прямыми способами. Основное достоинство этого подхода — его простота.

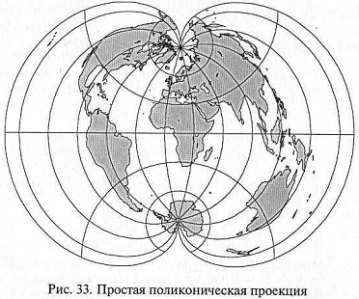
Поликоническая картографическая проекция — проекция, в которой параллели нормальной сетки — дуги эксцентрических окружностей, осевой меридиан — прямая, на которой расположены центры параллелей, остальные меридианы — кривые линии. По характеру искажений поликонические проекции разделяют на равновеликие, произвольные и равноугольные. Наибольшее практическое значение имеют произвольные и равноугольные поликонические проекции.

Простая поликоническая проекция - так называют проекцию, разработанную в США. Она известна также как «американская» проекция. Простую поликоническую проекцию можно представить как состоящую из таких участков конических проекций, в которых каждая параллель является главной. Поэтому в простой поликонической проекции на любой параллели нет искажений длин. Однозначно определен и радиус каждой параллели на карте. Искажений длин нет также на среднем прямолинейном меридиане. Центры окружностей, изображающих на карте параллели, расположены на среднем прямолинейном меридиане.

Рис. Простая поликоническая проекция

Существенным недостатком простой поликонической проекции является большая кривизна ее параллелей, особенно в высоких широтах. Другим недостатком являются значительные искажения длин, углов и площадей на тех участках, которые расположены по краям проекции в удалении от среднего меридиана.

Эти недостатки не позволяют применять простую поликоническую проекцию для отображения всей земной поверхности. Однако она удачно использована при построении отдельных листов многолистной Международной карты мира масштаба 1:1000000. Среди поликонических проекций особо выделяют круговые —проекции, в которых и меридианы, и параллели являются дугами окружностей, а экватор и средний меридиан — прямые линии. К этому типу принадлежит равноугольная поликоническая проекция Лагранжа. В 1772 г. немецкий ученый И.Г.Ламберт предложил равноугольное отображение мира в круге. Эту проекцию обычно называют проекцией Лагранжа. Поликонические проекции с параллелями переменной кривизны. В этих проекциях параллели обычно изображаются эллипсами, реже — другими плоскими кривыми. Меридианы — прямые или кривые линии. Известны предложения подобных проекций для карт России, карт Мирового океана и др.