7. Коэффициент конических проекций α, его параметры и крайние значения. Виды проекций при крайних значениях коэффициента α. Построение нормальной равнопромежуточной конической проекции.
В
нормальных конических проекциях
меридианы изображаются прямыми линиями,
сходящимися в одной точке под углами,
пропорциональными разностям
соответствующих долгот, а параллели—дугами
концентрических окружностей с центром
в точке схода меридианов. В косых и
поперечных проекциях такой же вид имеют
вертикалы и альмукантараты, а меридианы
и параллели изображаются сложными
кривыми. Практическое применение
получили в основном нормальные конические
проекции.
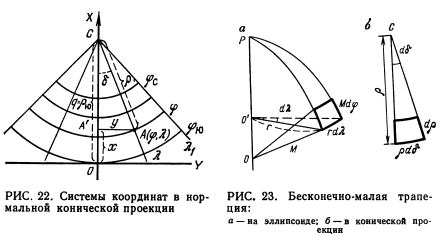Уравнения
конических проекций в общем виде
выражают в плоских прямоугольных у) и
полярных координата х (о — поляр –
ный радиус, б — полярный угол). За полюс этих координат принимается точка пересечения меридианов, за полярную ось — средний меридиан, от которого ведется счет разностей долгот X (рис. 22). За начало прямоугольных координат примем точку О, расположенную на среднем меридиане к югу от южной параллели карты, тогда
где
q = const — расстояние между полюсом
полярных и началом прямоугольных
координат; р — радиус параллели,
являющейся функцией только широты.
Параметр α всегда меньше единицы, т. е.
параллели изображаются неполными
окружностями. Если α= 1, то конические
проекции превращаются в азимутальные,
если α = 0 — в цилиндрические проекции.
В конической проекции у полюсов имеются
разрывы. Это обусловлено тем, что полный
круг долгот (от - π до +π) отображается
в сектор, угловая величина которого
всегда меньше 2 π. Поэтому на карте углы
между линиями меридианов не равны
соответствующей разности долгот, а
лишь пропорциональны ей.
Рис. Вариант произвольной норм. конической проекции (параметр α = 0,8)
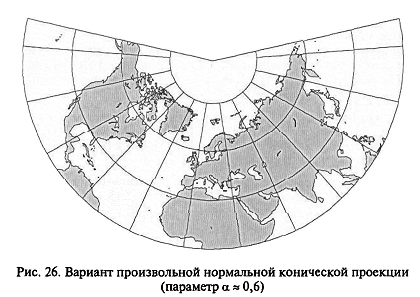
Рис. Вариант произв. кон. проекции (параметр α = 0,6)
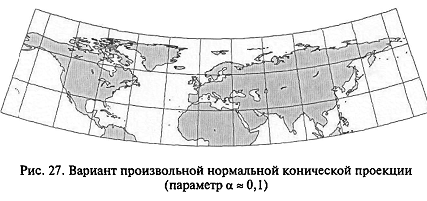
Рис. Вариант произв. норм. кон. проекции (парметр α = 0,1) |
Коэффициент пропорциональности а определяет степень сжатия круга и сектор и является важным параметром конических проекций. Его значения находятся в пределах 0 < α < 1. С приближением значения параметра α к 1 коническая проекция все больше становится похожей на азимутальную проекцию. В пределе при α = 1 коническая проекция превращается в азимутальную проекцию. С другой стороны, по мере приближения параметра α к 0 кривизна параллелей уменьшается, параллели выпрямляются, вид проекции все больше похож на вид цилиндрической проекции. |
В пределе при α = 0 коническая проекция превращается в цилиндрическую проекцию. Следовательно, азимутальные и цилиндрические проекции — суть предельные случаи конических проекций.
В каждой конической проекции имеются одна или две главные параллели, на которых сохраняется главный масштаб и, следовательно, нет искажений. Значения параметра α зависят от широт главных параллелей. Чем их широты ближе к экваториальным, тем α ближе к 0. С другой стороны, чем широты главных параллелей ближе к полярным, тем параметр α ближе к 1.
Конические проекции могут быть равнопромежуточными вдоль меридианов и вдоль параллелей. Практически используются только первые. В них m=1
Из
формулы
получаем
Интегрирование этого уравнения дает
где s-
длина дуги меридиана от экватора до
данной параллели; k
– параметр, выражающий радиус экватора
в проекции. Так как при ɸ=90 k≠s
, полюс изображается в этих проекциях
дугой окружности с радиусом
.
Подставив полученное значение ρ в
формулу
частного масштаба длин вдоль параллелей,
получаем
где
α- второй постоянный параметр
рассматриваемых конических проекций,
принимающий значения α˂1. При α=1 –
проекция будет равнопромежуточной
вдоль меридианов азимутальной проекцией
эллипсоида. При α=0 – равнопромежуточный
вдоль меридианов цилиндрической
проекцией эллипсоида. В зависимости
от получения параметров α
и k
находят различные равнопромежуточные
вдоль меридианов конические проекции.
-------------------------------------------------------------------------------------------------------