Искажения.

• За исключением центра, все формы искажены. Искажение возрастает по направлению от центра.

• Искажение площадей возрастает по направлению от центральной точки.

• Истинные направления по направлению от центральной точки.

• Расстояния для всех ориентировок точны по направлению от центра. Для полярной ориентировки расстояния вдоль меридианов точны, но существует модель увеличения искажения вдоль окружностей широты по направлению от центральной точки.

Обычно азимутальные проекции охватывают 90 градусов от центра, хотя можно спроецировать весь Земной шар. Полярные проекции лучше всего подходят для высокоширотных регионов с широтой выше 60 градусов, что обеспечивает минимальное искажение.

Области использования. Маршруты воздушной и морской навигации. Центральный объект располагается в центральной точке карты, с использованием соответствующей ориентировки проекции.

Полярные проекции - карты полярных регионов и маршрутов полярной навигации.

Экваториальные проекции - Местоположения на экваторе или вблизи него, например, Сингапур.

Косые проекции - Территории между полюсами и экватором, например, крупномасштабное картографирование Микронезии.

Если эта проекция используется для всего Земного шара, то проекция внутреннего полушария напоминает Азимутальную проекцию Ламберта. Внешнее полушарие значительно искажает формы и площади. В крайнем случае, полярная проекция, центрированная по Северному полюсу, представит Южный полюс как свою самую большую и наиболее удаленную окружность. Функция этой экстремальной проекции заключается в том, что независимо от равноугольного и площадного искажения, сохраняется точность представления расстояния и направления от центральной точки.

-------------------------------------------------------------------------------------------------------

54. Определить и обосновать группу проекций по показателям со следующими значениями m=1,14, n=1,14, 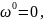p=1,2996.

Учение об искажениях занимает центральное место в теории картографических проекций. Ни сферу, ни поверхность эллипсоида невозможно расправить в плоскость — какие-то их участки будут сжаты, другие — растянуты. В плоскости, в общем случае, длины отрезков, углы между направлениями, формы участков и их площади не будут равны таковым на исходной поверхности. Они будут в той или иной степени искажены. При этом все виды искажений на карте взаимосвязаны и изменения одних влекут за собой изменения других.

Искажения длин на карте выражаются в том, что масштаб длин меняется с переменой места точки. Вследствие этого на карте неправильно передаются соотношения линейных размеров разных географических объектов. Об искажениях длин легко судить по частным масштабам длин. В бесконечно малой окрестности каждой точки карты различают:

m — частный масштаб длин по меридиану;

n — частный масштаб длин по параллели.

По определению, частный масштаб равен отношению длин малого (строго говоря, бесконечно малого) отрезка карты к соответствующему отрезку, вычисленному для эллипсоида или шара и выраженному в главном масштабе.

Частный масштаб площади может быть определен по формуле:

p = mn sinθ.

Таким образом, частный масштаб площади для каждой точки карты может быть вычислен путем определения частных масштабов длин по меридиану, по параллели и измерением угла между ними.

Наибольшие искажения углов. Разные углы, имеющие вершину в заданной точке, искажаются по-разному. Так, углы между главными направлениями не искажаются вовсе. Поэтому оцениваются максимальные искажения (ω), которые вычисляют по формуле:

Первое, на что стоит обратить внимание в данном нам условии: ω = 0. Это свойство присуще только группе равноугольных проекций.

В равноугольных проекциях картографическая сетка ортогональна, частные масштабы длин не зависят от направлений, т.е. m = n = a = b = μ, но имеются большие искажения площадей.

---------------------------------------------------------------------------------------------------------

55. Определить и обосновать группу проекций по показателям со следующими значениями m=0,86, n=1,14, 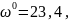p=1,2996.

Учение об искажениях занимает центральное место в теории картографических проекций. Ни сферу, ни поверхность эллипсоида невозможно расправить в плоскость — какие-то их участки будут сжаты, другие — растянуты. В плоскости, в общем случае, длины отрезков, углы между направлениями, формы участков и их площади не будут равны таковым на исходной поверхности. Они будут в той или иной степени искажены. При этом все виды искажений на карте взаимосвязаны и изменения одних влекут за собой изменения других.

Искажения длин на карте выражаются в том, что масштаб длин меняется с переменой места точки. Вследствие этого на карте неправильно передаются соотношения линейных размеров разных географических объектов. Об искажениях длин легко судить по частным масштабам длин. В бесконечно малой окрестности каждой точки карты различают:

m — частный масштаб длин по меридиану;

n — частный масштаб длин по параллели.

По определению, частный масштаб равен отношению длин малого (строго говоря, бесконечно малого) отрезка карты к соответствующему отрезку, вычисленному для эллипсоида или шара и выраженному в главном масштабе.

Частный масштаб площади может быть определен по формуле:

p = mn sinθ.

Таким образом, частный масштаб площади для каждой точки карты может быть вычислен путем определения частных масштабов длин по меридиану, по параллели и измерением угла между ними.

Наибольшие искажения углов. Разные углы, имеющие вершину в заданной точке, искажаются по-разному. Так, углы между главными направлениями не искажаются вовсе. Поэтому оцениваются максимальные искажения (ω), которые вычисляют по формуле:

В нашем случае m ≠ n ≠ 1, следовательно проекция не равнопромежуточная.

ω ≠ 0, следовательно проекция не равноугольная.

р ≠ 1, так что проекция не равновеликая.

Таким образом, согласно данным значениям m, n, ω и p, можно сделать вывод, что в этой группе проекций присутствуют искажения всех видов, т.е. по характеру искажений проекции произвольные.

--------------------------------------------------------------------------------------------------------

56. Определить радиус модели земного шара (R₀) и радиус параллели (r) на широте 45⁰ в масштабе 1:5 000 000. Изменение коэффициента «α» конических проекций. С какими проекциями связаны его крайние значения?

Чтобы вычислить радиус модели земного шара, воспользуемся формулой

R₀ = R_З · M.

Подставляем значения в формулу (радиус Земли переводим в см):

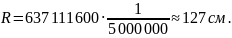
Для того чтобы определить радиус параллели на широте 45⁰ в конической проекции, необходимо знать параллель касания (секущие параллели). Данные нужно подставить в формулу:

ρ = ρ₀ – R(φ – φ₀)

В конической проекции у полюсов имеются разрывы. Это обусловлено тем, что полный круг долгот (от -π до +π) отображается в сектор, угловая величина которого всегда меньше 2π. Поэтому на карте углы между линиями меридианов не равны соответствующей разности долгот, а лишь пропорциональны ей. Коэффициент пропорциональности α определяет степень сжатия круга и сектор и является важным параметром конических проекций. Его значения находятся в пределах 0 < α < 1.

С приближением значения параметра α к 1 коническая проекция все больше становится похожей на азимутальную проекцию. В пределе при α = 1 коническая проекция превращается в азимутальную проекцию. С другой стороны, по мере приближения параметра α к 0 кривизна параллелей уменьшается, параллели выпрямляются, вид проекции все больше похож на вид цилиндрической проекции. В пределе при α = 0 коническая проекция превращается в цилиндрическую проекцию. Следовательно, азимутальные и цилиндрические проекции — есть предельные случаи конических проекций.

В каждой конической проекции имеются одна или две главные параллели, на которых сохраняется главный масштаб и, следовательно, нет искажений. Значения параметра а зависят от широт главных параллелей. Чем их широты ближе к экваториальным, тем а ближе к 0. С другой стороны, чем широты главных параллелей ближе к полярным, тем параметр а ближе к 1.

--------------------------------------------------------------------------------------------------------