48.Построение сетки нормальной цилиндрической проекции, пространственное изменение эллипса искажений. Показатель, объединяющий азимутальные, конические и цилиндрические проекции.

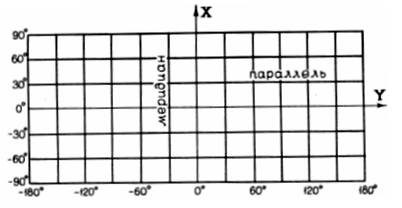
Нормальная сетка цилиндрических проекций имеет простой вид: все меридианы — параллельные прямые, расположенные на одинаковом расстоянии друг от друга, параллели — прямые, перпендикулярные к меридианам; расстояния между ними изменяются в зависимости от свойств проекции. Прямоугольные координаты этих проекций: х = / (ф); у = рА, , где параметр проекции р = const.

За ось X выбирают один из меридианов, за ось Y — экватор или одну из параллелей (рис. 35).

Рис. Вид сетки норм. цилиндр. проекции

Функцию, определяющую абсциссу проекции, находят под условием равноугольности, равно-великости или равнопромежуточности изображения; соответст-венно и цилиндрические проекции могут быть равноугольными, равно-великими или равнопромежуточными по меридианам.

Кроме перечисленных проекций в картографической практике встречаются также произвольные по характеру искажений проекции (с заданным распределением искажений и перспективно-цилиндрические проекции,получаемые геометрическим путем).

Картографируемую поверхность принимают в этих проекцияхза эллипсоид или за сферу.

Главные направления в нормальных цилиндрических проекцияхсовпадают с меридианами и параллелями,поэтому масштабы померидианам и параллелям являются экстремальными.

Общие формулы нормальных цилиндрических проекций эллипсоида:

Наиболее полно виды искажений можно представить с помощью эллипса искажений. В теории картографических проекций доказывается, что бесконечно малая окружность на поверхности эллипсоида в общем случае изобразится на плоскости эллипсом, называемым эллипсом искажения.

Данным показателем является параметр α всегда меньше единицы, т. е. параллели изображаются неполными окружностями. Если α= 1, то конические проекции превращаются в азимутальные, если α = 0 — в цилиндрические проекции. В конической проекции у полюсов имеются разрывы. Это обусловлено тем, что полный круг долгот (от - π до +π) отображается в сектор, угловая величина которого всегда меньше 2 π. Поэтому на карте углы между линиями меридианов не равны соответствующей разности долгот, а лишь пропорциональны ей. Коэффициент пропорциональности α определяет степень сжатия круга и сектор и является важным параметром конических проекций. Его значения находятся в пределах. Следовательно, азимутальные и цилиндрические проекции — есть предельные случаи конических проекций.

---------------------------------------------------------------------------------------------------------

49.Построение сетки нормальной конической (на касательном конусе) проекции, пространственное изменение эллипса искажений. Показатель, объединяющий азимутальные, конические и цилиндрические проекции

Название свое конические проекции получили от конуса, поверхность которой используется в качестве промежуточной при проектировании земной поверхности на плоскость. В этих проекциях параллели нормальной сетки – дуги концентрических окружностей, а меридианы – их радиусы, углы между

которыми пропорциональны соответствующим разностям долгот.

Более полную и наглядную характеристику искажений дает эллипс искажений, который иначе называют индикатрисой Тиссо. Эллипс искажений в данной точке карты изображает бесконечно малый круг на поверхности эллипсоида или шара. Полуоси эллипса равны экстремальным масштабам длин а и b; они ориентированы по главным направлениям. Радиус – вектор эллипса по любому направлению определяет частный масштаб длин и, следовательно, характеризует искажения длин. Форма эллипса показывает искажения углов и форм – они искажены тем больше, чем больше эллипс отличается от окружности. Площадь эллипса пропорциональна искажению площадей и тем она больше, чем больше искажены площади.

Коэффициент пропорциональности долгот α определяет степень сжатия круга в сектор и является важным параметром конических проекций. Его значения находятся в пределах: 0<α<1. С приближением параметра α к единице коническая проекция становится все больше похожей на азимутальную проекцию. При α=1 коническая превращается в азимутальную

проекцию. С другой стороны, по мере приближения параметра α к нулю кривизна параллелей уменьшается, проекция все больше походит на цилиндрическую. В пределе при α=0 коническая проекция превращается в цилиндрическую проекцию. Значения параметра α зависят от широт главных параллелей (на них сохраняется главный масштаб). Чем ближе широты главных параллелей к полюсу, тем параметр α ближе к 1 и наоборот.

---------------------------------------------------------------------------------------------------------

50.Построение сетки нормальной азимутальной проекции, пространственное изменение эллипса искажений. Показатель, объединяющий азимутальные, конические и цилиндрические проекции.

Азимутальные, когда проектирование эллипсоида осуществляется на касательную или секущую его плоскость. В этих проекциях меридианы нормальной сетки изображаются прямыми, исходящими из одной точки под углами, пропорциональными разности долгот, а параллели – концентрическими окружностями с центром в точке пересечения меридианов.

Данным показателем является параметр α всегда меньше единицы, т. е. парал-лели

изображаются неполными окружностями. Если α= 1, то конические проекции превращаются в азимутальные, если α = 0 — в цилиндрические проекции. Коэффициент пропорциональности а определяет степень сжатия круга и сектор и является важным параметром конических проекций. Чтобы наглядно продемонстрировать искажения,Тиссо предложил использовать специальные эллипсы искажений (индикатриссы), которые представляют собой бесконечно малые эллипсы в любой точке карты, являющиеся отображением бесконечно малых окружностей в соответствующей точке на поверхности земного эллипсоида или шара. Эллипс становится шаром в точке (линии) нулевых искажений. Изменение формы эллипса отражает степень искажения углов и растояний, а размера - степень искажения площадей. и установим, что исследуемая кривая является эллипсом.

P.S. Эллипсы искажений на азимутальной проекции нарисуйте сами..

-----------------------------------------------------------------------------------------------------

51. Количество главных параллелей в нормальных конических проекциях, построенных на касательном и секущем конусах, величина искажений по ним. Какое значение определяется зависимостью) ρ=R· в нормальной равнопромежуточной конической проекции (на касательном конусе)?

Коническая картографическая проекция — проекция, в которой параллели нормальной сетки — дуги концентрических окружностей, а меридианы — их радиусы, углы между которыми пропорциональны соответствующим разностям долгот.

Коническая проекция может быть построена на касательном или секущем конусе. В конической равнопромежуточной проекции все параллели находятся на равном расстоянии друг от друга, пересекая меридианы через одинаковые интервалы. Это утверждение является верным, независимо от того, одна или две параллели используются в качестве стандартных параллелей.

Пересекающиеся линии координатной сетки разнесены на одинаковые расстояния. Расстояние между каждым меридианом одинаково, как и расстояние между каждой из концентрических дуг, описывающих линии широты. Полюса представлены скорее как дуги, чем как точки.

Если две стандартные параллели расположены симметрично к северу и к югу от экватора, то результирующая проекция будет такой же, как и проекция равных прямоугольников, и следует использовать именно её. В этом случае следует использовать проекцию равных прямоугольников. Проекция равных прямоугольников применяется также, если стандартной параллелью является экватор.

Для простых конических проекций на касательном конусе: Для определения вида функции ρ = f (φ) поставим условие равнопромежуточности по меридианам m=1, или приняв главный масштаб равным единице µ ₀ = 1 , получим : m=µ₁/ µ₀ = -αρ/Rd φ / µ₀ = - αρ/ µ0 Rd φ = - αρ/ 1· Rdφ, т.к. m=1 , то 1= - αρ/ Rdφ, отсюда αρ= - Rd φ.

Интегрируя, т.е. обобщая последнее выражение, получаем:

ρ=R·φ+ρ _экв = ρ _экв - R· φ, где φ выражена в радианах.

Произведение R· φ= x представляет длину дуги меридиана от экватора до параллели с широтой φ. ρ_экв – расстояние интегрирования.

Геометрический смысл ρ_экв – он представляет собой изображения экватора на карте. Если φ=0, то ρ = ρ_экв.

В равнопромежуточных конических проекциях полюс также изобразится дугою окружности, его формула ρ = ρ_экв - R·π /2

Для масштаба вдоль параллели будем иметь n= αρ / r = α ( ρэкв -Rφ) / µ₀Rcosφ

Для радиуса параллели с наименьшим масштабом будеи иметь: , т.к. m=1, а

для можно применить формулу , тогда , отсюда

По формуле , в которой , можно определить коэффициент пропорциональности долгот на карте:

После чего по формуле δ = αλ ( см. начало лекции) вычислить долготы на карте можно по

формуле:

Искажения

Локальные формы являются истинными вдоль стандартных параллелей. Искажение постоянно вдоль любой данной параллели, но увеличивается по мере удаления от стандартных параллелей.

Искажение площадей постоянно вдоль любой данной параллели, но увеличивается по мере удаления от стандартных параллелей.

Направление локальное – истинное вдоль стандартных параллелей.

Расстояние Истинное вдоль меридианов и стандартных параллелей. Масштаб постоянен вдоль любой данной параллели, но изменяется от параллели к параллели.

Проекция применяется для картографирования регионов, расположенных в средних широтах, вытянутых в направлении с востока на запад.

Обычно используется для карт в атласах небольших стран.

Использовалась в Советском Союзе для картографирования всей страны. В СССР применялись специально разработанные проекции Каврайского, Красовского и ряд других со стандартными параллелями 47° и 62° СШ и центральным меридианом 100° ВД. Проекция Красовского отличалась уменьшенным масштабом по меридиану, m = 0,997.

--------------------------------------------------------------------------------------------------------