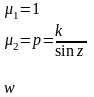- •1. Предмет и задачи математической картографии. Геодезическая основа карт, ее значение.
- •2. Относительные поверхности, используемые при построении карт. Географическая сетка, ее составные части и их определение.
- •3. Определение главных масштабов длин и площадей. Полярные сферические координаты в системе нормальной, косой и поперечной проекций.
- •5. Главные параллели, причины их возникновения. Показатели искажений форм и углов. Классификация проекций по видам искажений.
- •6.Общая теория азимутальных проекций. Вид картографической сетки азимутальной, псевдоазимутальной проекций, их характеристика.
- •7. Коэффициент конических проекций α, его параметры и крайние значения. Виды проекций при крайних значениях коэффициента α. Построение нормальной равнопромежуточной конической проекции.
- •8. Общая теория цилиндрических проекций. Уравнения цилиндрических проекций.
- •9. Прямые способы построения картографических проекций. Вид картографической сетки поликонической проекции.
- •10.Отличительные свойства стереографической и ортографической перспективных азимутальных проекций.
- •11. Уравнения конических проекций. Равноугольные конические проекции шара, их использование.
- •12. Уравнения азимутальных проекций. Равновеликие азимутальные проекции. Перспективные азимутальные проекции, их применение.
- •13. Нормальные цилиндрические проекции карт мира. Равновеликие цилиндрические проекции, их применение.
- •14. Картографические проекции карт восточного и западного полушарий.
- •15. Проекции, показывающие сферичность полушарий Земли.
- •16. Распознавание картографических проекций. Определение проекции и ее данных по карте. Карты Казахстана в нормальной равноугольной конической проекции.
- •17. Поликонические проекции карт мира. Построение и использование нормальной квадратно-цилиндрической проекции.
- •19. Признаки классификации картографических проекций. Признаки распознавания картографических проекций, их характеристика.
- •20. Показатели искажений, их определение на карте. Условия выбора картографических проекций.
- •21. Общая теория конический проекций. Карты Казахстана в нормальной равновеликой конической проекции.
- •22.Общая теория цилиндрических проекций. Равноугольные цилиндрические проекции. Виды цилиндрических проекций, их использование.
- •23. Равновеликие проекции шара, их использование. Построение равнопромежуточной азимутальной проекции Постеля.
- •24. Общие формулы нормальных азимутальных проекций. Косые азимутальные проекции, их применение.
- •25. Значение картографических проекций, примеры их уравнений
- •27. Изоколы. Виды изокол основных г-рупп проекций. Формулы нормальной равноугольной азимутальной проекции шара.
- •28. Основные направления любой точки карты, их смысл и значения.
- •29. Виды сеток конических псевдоконических и поликонических проекций, их характеристика.
- •30. Классификация проекций по виду нормальной картографической сетки.
- •Классификация проекций по виду нормальной картографической сетки
- •32. Отличительные свойства цилиндрических проекций Меркатора и Ламберта.
- •33. Равнопромежуточные конические проекции шара, их практическое использование.
- •37. Построение нормальной равнопромежуточной конической проекции с приведением используемых необходимых показателей.
- •41. Построить сетку и изоколы нормальной азимутальной проекции на секущей плоскости. Отметить места отсутствия искажений.
- •44.Построение сетки и изоколов нормальных цилиндрических, косых и поперечных азимутальных проекций.
- •45.Построение сетки цилиндрической и псевдоцилиндрической проекций, их практическое использование.
- •46. Главный масштаб карты ( µ0) равен 1, 5, 50, 200, ∞. Выберите и обоснуйте правильный ответ.
- •47.Частные масштабы карты равны 1, 5, 20, 100, ∞. Выберите и обоснуйте правильный ответ.
- •48.Построение сетки нормальной цилиндрической проекции, пространственное изменение эллипса искажений. Показатель, объединяющий азимутальные, конические и цилиндрические проекции.
- •52. Количество главных параллелей в нормальных цилиндрических проекциях, построенных на касательном и секущем цилиндрах, величина искажений по ним.
- •Проекция равных прямоугольников, или простая цилиндрическая
- •53. Количество главных параллелей в нормальных азимутальных проекциях, построенных на касательной и секущей плоскостях, величина искажений по ним.
- •Искажения.
- •За исключением центра, все формы искажены. Искажение возрастает по направлению от центра.
- •Истинные направления по направлению от центральной точки.
- •Области использования. Маршруты воздушной и морской навигации. Центральный объект располагается в центральной точке карты, с использованием соответствующей ориентировки проекции.
- •57. Какие показатели необходимо определить при построении карты Казахстана в нормальной конической проекции (на касательном конусе) в масштабе 1:10 000 000 ?
- •59. Формулы, используемые при определении дуг меридианов и параллелей. Что определяется зависимостью в нормальной равнопромежуточной конической проекции (на касательном конусе)?
- •60. В каких проекциях значения искажений равны ∞, его причины?
44.Построение сетки и изоколов нормальных цилиндрических, косых и поперечных азимутальных проекций.
Для изображения территорий, расположенных в приэкваториальной зоне (приблизительно симметрично относительно экватора), выбирают нормальные цилиндрические проекции. В нормальных цилиндрических проекциях изоколы имеют вид прямых линий, совпадающих с параллелями. В поперечных и косых цилиндрических проекциях изоколы – прямые, параллельные прямолинейному осевому меридиану (в поперечных проекциях) или изображающейся прямой линией дуге большого круга, проходящей через середину территории (в косых проекциях).
В косых и поперечных цилиндрических проекциях величины искажений вычисляются так же, как и в азимутальных проекциях в зависимости от зенитного расстояния z.
Для этого на схеме компоновки проводят две граничные изоколы z гр косой (поперечной) цилиндрической проекции и между ними экватор косой системы координат z экв = 900.
Зенитное расстояние для граничных изокол вычисляется по формуле: z гр = 900 - z, где z в градусах определяется путем измерения по прямолинейному осевому меридиану.
Если территория достаточно узкая (небольшое расстояние между граничными изоколами), то ставится условие сохранения масштаба длин на экваторе косой системы координат (z k = 900). В противном случае ставится условие сохранения масштаба длин на изоколе с z k (900 + z гр) / 2 (рис. 7).
Формулы для вычисления искажений в цилиндрических проекциях приведены ниже:
Равноугольная |
|
|
Равновеликая |
|
|
Равнопромежуточная |
вдоль меридианов |
|
|
|
|
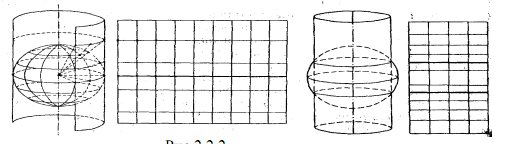
Косая равнопромежуточная вдоль вертикалов цилиндрическая проекция. Пример.
Вычисление масштабов и искажений для косой равнопромежуточной вдоль вертикалов цилиндрической проекции.
Для территории, изображенной на рисунке, имеем:
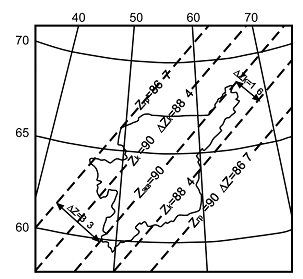
z
гр
= 3,30;
z
гр
= 900
-
z
гр
= 900
– 3,30
= 86,70.
z
гр
= 3,30;
z
гр
= 900
-
z
гр
= 900
– 3,30
= 86,70.
z k (900 +z гр) /2 = (900 + 86,70) /2 88,40.
По формулам из приложения 2 вычисляем:
 .
.
Масштабы и искажения |
z = 900 |
z k = 88,40 |
z гран = 86,70 |
|
1,0000
0,9996
00 01,3 |
1,0000
1,0000
00 |
1,0000
1,0013
00 04,4 |
---------------------------------------------------------------------------------------------------------
45.Построение сетки цилиндрической и псевдоцилиндрической проекций, их практическое использование.
Цилиндрическая картографическая проекция — проекция, в которой параллели нормальной сетки — параллельные прямые, а меридианы — перпендикулярные параллелям прямые, расстояния между которыми пропорциональны разностям долгот. Проекция может иметь одну или две главные параллели (альмукантараты), на которых отсутствуют искажения.В цилиндрических поверхность эллипсоида переносится на
боковую поверхность касательного рис(1а) или секущего рис(1б) цилиндра, после чего последний разрезается по образующей и развертывается в плоскость.
В этих проекциях меридианы изображаются равноотстоящими
параллельными прямыми, а параллели также прямыми, перпендикулярными к
меридианам . Частные масштабы зависят только от широты, поэтому изоколы совпадают с параллелями и имеют вид прямых. Нормальные цилиндрические проекции выбирают для изображения территорий, расположенных в приэкваториальной зоне (приблизительно симметрично относительно экватора),
Рис. Псевдоцилиндрические проекции. Равновеликая синусоидальная проекция В. В. Каврайского |
Псевдоцилиндрическая картографическая проекция — проекция, в которой параллели нормальной сетки — параллельные прямые, средний меридиан — прямая, перпендикулярная параллелям, а остальные меридианы — ломаные прямые или кривые. |
Псевдоцилиндрические, в которых параллели прямые линии, перпендикулярные к прямолинейному осевому меридиану, остальные меридианы – кривые (синусоиды, эллипсы), симметричные относительно осевого. Псевдоцилиндрические проекции в основном применяются для отображения в мелком масштабе крупных частей шарообразной планеты или всей ее поверхности. Поэтому в псевдоцилиндрических проекциях земная поверхность принимается за поверхность шара.
--------------------------------------------------------------------------------------------------------