29. Виды сеток конических псевдоконических и поликонических проекций, их характеристика.
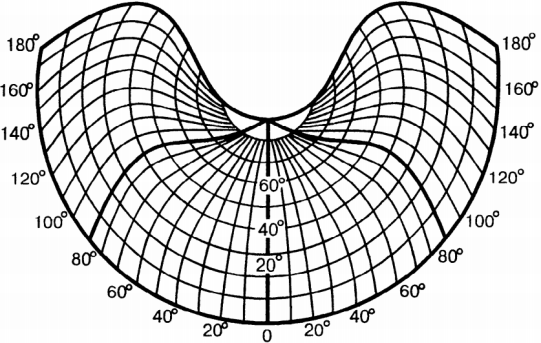
Псевдоконические проекции. Псевдоконическая картографическая проекция — проекция, в которой параллели нормальной сетки — дуги концентрических окружностей, осевой меридиан — прямая, на которой расположен центр параллелей, остальные меридианы — кривые.
Рис. Псевдоконическая проекция |
Общие уравнения этих проекций имеют вид x = q – ρ cosδ; y = ρ sinδ; ρ = f(φ); δ = F(φ, λ), где q=const – полярное расстояние южной параллели на плоскости.
|
Следовательно, эти проекции не могут быть равноугольными и сохранять длины вдоль меридианов. Они могут быть только равновеликими и произвольными по характеру искажений.
В частном случае, при δ = αλ или δ = λ меридианы – прямые линии и проекции соответственно будут коническими или азимутальными. Если центр параллелей удалисть в бесконечность, то параллели обратятся в параллельные прямые – проекция станет псевдоцилиндрической.
Наибольшее применение из псевдоконических получила равновеликая проекция Бонна, которая была предложена им в 1752 г. для создания карты Франции.
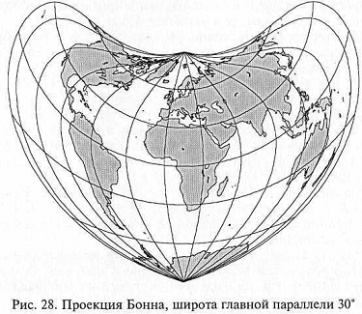
Проекция Бонна равновеликая. Главный масштаб сохраняется на среднем меридиане и на всех параллелях. Параллели под прямым углом пересекают только средний меридиан. Однако имеется одна параллель, пересекающая все меридианы под прямым углом. Ее условно назовем главной параллелью проекции Бонна. На рис., где отображена проекция Бонна, широта этой параллели 30°.
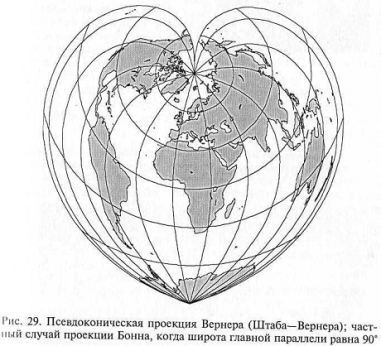
Псевдоконическая проекция Штаба-Вернера (сердцевидная). Была предложена в начале 16 в. В проекции нет искажений на среднем меридиане и северном полюсе. При удалении от них искажения сильно возрастают, достигая наибольших значений на параллели, близкой к южному полярному кругу.
Поликонические проекции. Поликоническая картографическая проекция — проекция, в которой параллели нормальной сетки — дуги эксцентрических окружностей, осевой меридиан — прямая, на которой расположены центры параллелей, остальные меридианы — кривые линии.
По характеру искажений поликонические проекции разделяют на равновеликие, произвольные и равноугольные. Наибольшее практическое значение имеют произвольные и равноугольные поликонические проекции. Известны также теоретические исследования Н.А.Урмаева, Л.М.Бугаевского и других ученых, посвященные разработке теории равновеликих проекций.
Простая
поликоническая проекция
— так называют проекцию, разработанную
в США, где для составления топографических
карт ее применяли вплоть до 1950 г. Простую
поликоническую проекцию можно представить
как состоящую из таких участков
конических проекций, в которых каждая
параллели является главной. Поэтому в
простой поликонической проекции на
любой параллели нет искажений длин.
Однозначно определен и радиус каждой
параллели на карте. Искажений длин нет
также на среднем прямолинейном меридиане.
Центры окружностей, изображающих на
карте параллели, расположены на среднем
прямолинейном меридиане.
Трудами известных ученых ЦНИИГАиК Н.А.Урмаева, Т.Д. Салмановой и Г.А. Гинзбурга разработан ряд новых поликонических проекций, нашедших применение при создании настенных карт и карт атласов. Эти проекции обычно известны как поликонические проекции ЦНИИГАиК. На рис. 34 приведена одна из проекций, использовавшаяся для построения многочисленных тематических карт для высшей школы в масштабе 1:15 000 000.
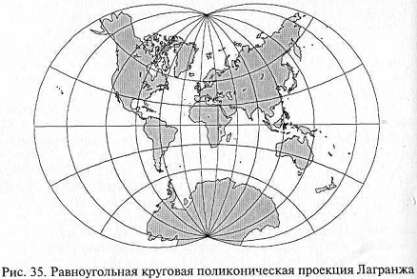
Среди поликонических проекций особо выделяют круговые — проекции, в которых и меридианы, и параллели являются дугами окружностей, а экватор и средний меридиан — прямые линии. К этому типу принадлежит равноугольная поликоническая проекция Лагранжа, приведенная на рис. 35.
--------------------------------------------------------------------------------------------------------