27. Изоколы. Виды изокол основных г-рупп проекций. Формулы нормальной равноугольной азимутальной проекции шара.
Применяют разные способы для демонстрации искажений на картах — профили головы человека, изоколы, эллипсы искажений и др. Эти способы должны быть наглядными и, по возможности, простыми. Распространен способ изокол.
Изокола — линия равных значений показателей, характеризующих искажения на карте.
Изоколы строятся для любых показателей искажений: длин, площадей, углов, форм. Изоколы характеризуют искажения отдельных видов. Они получили распространение благодаря простоте построения. Изоколы удобны тем, что по ним видно, как и в каких направлениях нарастают или убывают искажения и где на карте наибольшие или наименьшие их значения.
|
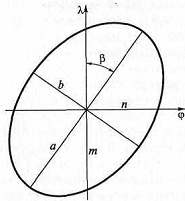
Более полную и наглядную характеристику искажений дает эллипс искажений; иначе его называют индикатрисой Тиссо.
Рис. Эллипс искажений (индикатрисаТиссо): a, b, m, n — частные масштабы длин, соответственно, наибольший, наименьший, по ме-ридиану, по параллели; (β — азимут на карте большой полуоси эллипса.
|
Эллипс искажений в данной точке карты изображает бесконечно малый круг на поверхности эллипсоида или шара. Радиус-вектор эллипса по любому направлению определяетчастный масштаб длин и, следовательно, характеризует искажения длин.
Форма эллипса иллюстрирует искажения углов и форм — они искажены тем больше, чем больше эллипс отличается от окружности.
Площадь эллипса пропорциональна искажению площадей и тем она больше, чем больше искажены площади. Таким образом, эл липе искажений является весьма наглядной локальной комплексной характеристикой всех видов искажений.
Стереографическая азимутальная проекция. Предложена известным астрономом Гиппархом. Главные свойства проекции изучал древнегреческий ученый Клавдий Птолемей. Проекция равноугольная. Как уже отмечалось, она обладает замечательным свойством: любая окружность на поверхности шара в этой проекции изображается окружностью. Благодаря этому свойству, ее используют не только в картографии, но и в далеких от нее областях знания, таких, как кристаллография, электротехника и др.
Данная проекция является частным случаем равноугольной конической проекции при а = 1.
Формулы
и
принимают вид
ρ = k/U; μ = μ1 = μ2 = k/rU; p = μ2; k = r0U0
где
;
r0,
U0
– определяются по заданной широте φ0
главной параллели, для которой частный
масштаб равен 1.
--------------------------------------------------------------------------------------------------------
28. Основные направления любой точки карты, их смысл и значения.
Длины отрезков, за исключением линий нулевых искажений, искажаются в любых проекциях. В каждой точке карты существуют два направления, по которым частные масштабы длин принимают экстремальные значения — по одному из них масштаб максимален, по другому — минимален. Значения азимутов этих направлений определяются формулой
Поскольку период тангенса равен π, то это уравнение дает два ответа: β и β + 90°. Это означает, что направления экстремальных масштабов являются взаимно перпендикулярными.
Главные направления в картографической проекции —два взаимно перпендикулярных напразления в каждой точке карты, по которым частные масштабы длин имеют наибольшее и наименьшее значения. Если на карте между меридианом и параллелью прямой угол (θ = 90°), то главные направления всегда
будут ориентированы по меридиану и параллели. Таким образом, в ортогональных проекциях экстремальными являются частные масштабы m и n.
Обычно экстремальные масштабы обозначаются буквами:
а — наибольший масштаб;
b — наименьший масштаб.
Из этого следует, что в ортогональных проекциях верны соотношения:
либо а = m, b = n;
либо а = n, b = m.
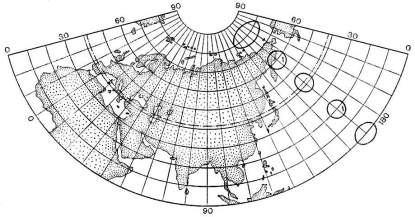
Рис. Пример главных направлений в конической проекции: главный меридиан (λ0 = 900) и одна главная параллель (φ0 = 450) [главный меридиан и гл. параллель нарисуйте сами]
--------------------------------------------------------------------------------------------------------