25. Значение картографических проекций, примеры их уравнений
Теория К. п. — Математическая картография — имеет своей целью изучение всех видов искажений отображений поверхности земного эллипсоида на плоскость и разработку методов построения таких проекций, в которых искажения имели бы или наименьшие (в каком-либо смысле) значения или заранее заданное распределение.
Исходя из нужд картографии, в теории К. п. рассматривают отображения поверхности земного эллипсоида на плоскость. Т. к. земной эллипсоид имеет малое сжатие, и его поверхность незначительно отступает от сферы, а также в связи с тем, что К. п. необходимы для составления карт в средних и мелких масштабах (М > 1 000 000), то часто ограничиваются рассмотрением отображений на плоскость сферы некоторого радиуса R, отклонениями которой от эллипсоида можно пренебречь или каким-либо способом учесть. Поэтому далее имеются в виду отображения на плоскость хОу сферы, отнесённой к географическим координатам φ (широта) и λ (долгота).
Уравнения любой К. п. имеют вид
x = f1(φ, λ), y = f2(φ, λ), (1) где f1 и f2 — функции, удовлетворяющие некоторым общим условиям. Изображения меридианов λ = const и параллелей φ = const в данной К. п. образуют картографическую сетку. К. п. может быть определена также двумя уравнениями, в которых фигурируют не прямоугольные координаты х, у плоскости, а какие-либо иные. Некоторые К. п. можно определить геометрическими построениями. К. п. определяют также правилом построения соответствующей ей картографической сетки или такими её характеристическими свойствами, из которых могут быть получены уравнения вида (1), полностью определяющие проекцию.
Наиболее общаими являются конические проекции, общие уравнения которых принимают вид
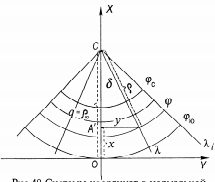
δ =α ·λ, ρ=f(φ),
В конической проекции у полюсов имеются разрывы. Это обусловлено тем, что полный круг долгот (от -π до +π) отображается в сектор, угловая величина которого всегда меньше 2π. Поэтому на карте углы между линиями меридианов не равны соответствующей разности долгот, а лишь пропорциональны ей. Коэффициент пропорциональности α определяет степень сжатия круга и сектор и является важным параметром конических проекций. Его значения находятся в пределах 0 < α < 1.
С приближением значения параметра α к 1 коническая проекция все больше становится похожей на азимутальную проекцию. В пределе при α = 1 коническая проекция превращается в азимутальную проекцию. С другой стороны, по мере приближения параметра α к 0 кривизна параллелей уменьшается, параллели выпрямляются, вид проекции все больше похож на вид цилиндрической проекции. В пределе при α = 0 коническая проекция превращается в цилиндрическую проекцию. Следовательно, азимутальные и цилиндрические проекции — есть предельные случаи конических проекций.
---------------------------------------------------------------------------------------------------------
26. Определение и характеристика проекции по следующим математическим зависимостям: δ=α∙λ; ρ=f(φ)
Проекции, принадлежащие к группе конических, являются наиболее общими. Теоретически можно показать, что проекции азимутальной и цилиндрической групп представляют собой крайние, предельные случаи группы конических проекций.
Во всех классах первого подмножества параллели на плоскости представляют собой дуги окружностей.
Рис. Системы координат в нормальной конической проекции
|
Коническими называют картографические проекции, в которых параллели изображаются концентрическими окружностями, а меридианы – пучком прямых, проведенных из центра окружностей. При этом углы в точке полюса междц меридианами на проекции и эллипсоиде (сфере) пропорциональны и, следовательно, на проекции в точке полюса возникает разрыв изображения.
|
Исходя из определения, общие уравнения проекции принимают вид
δ =α ·λ, ρ=f(φ),
В конической проекции у полюсов имеются разрывы. Это обусловлено тем, что полный круг долгот (от -π до +π) отображается в сектор, угловая величина которого всегда меньше 2π. Поэтому на карте углы между линиями меридианов не равны соответствующей разности долгот, а лишь пропорциональны ей. Коэффициент пропорциональности α определяет степень сжатия круга и сектор и является важным параметром конических проекций. Его значения находятся в пределах 0 < α < 1.
С приближением значения параметра α к 1 коническая проекция все больше становится похожей на азимутальную проекцию. В пределе при α = 1 коническая проекция превращается в азимутальную проекцию. С другой стороны, по мере приближения параметра α к 0 кривизна параллелей уменьшается, параллели выпрямляются, вид проекции все больше похож на вид цилиндрической проекции. В пределе при α = 0 коническая проекция превращается в цилиндрическую проекцию. Следовательно, азимутальные и цилиндрические проекции — есть предельные случаи конических проекций.
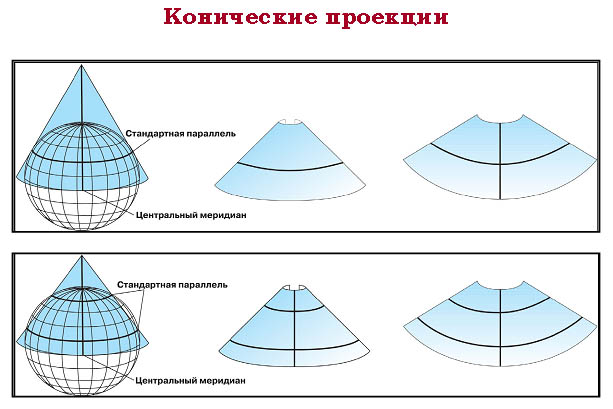
Рис. Построение коническое проекции на касательном и секущем конусах. |
В каждой конической проекции имеются одна или две главные параллели, на которых сохраняется главный масштаб и, следовательно, нет искажений. Значения параметра а зависят от широт главных параллелей. Чем их широты ближе к экваториальным, тем а ближе к 0. С другой стороны, чем широты главных параллелей ближе к полярным, тем параметр а ближе к 1. |
---------------------------------------------------------------------------------------------------------