21. Общая теория конический проекций. Карты Казахстана в нормальной равновеликой конической проекции.
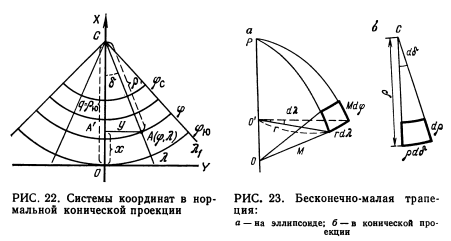
Конические проекции выражаются двумя следующими общими для всех конических проекций уравнениями: δ =α·λ; ρ=f(φ), из которых видно, что меридианы изображаются прямыми линиями, при этом долгота δ на карте пропорциональна долготе λ на глобусе, следовательно, если разность долгот между смежными меридианами на глобусе была одна и та же, то и угол между смежными меридианами на карте будет один и тот же.
Параллели
изображаются дугами концентрических
окружностей, радиусы которых ρ —
функция широты φ. При рассмотрении
того или иного частного случая
конических проекци необходимо
установить, во-первых, каков коэффициент
пропорциональности α долгот на карте
и, во-вторых, каков вид функции ρ=f(φ).
Продифференцируем эти формулы по ɸ и
α и полученные производные подставим
в формулы частных масштабов длин и
общей теории картографических
проекций.Тогда получим формулы частных
масштабов данного класса проекций
. Так как в этих проекциях меридианы и
параллели изображаются ортогонально,
то они совпадают с главными направлениями
в точках проекции и частные масштабы
m
и n
являются экстремальными.
Форма территории Казахстана, его долготная протяженность напоминают территорию Российской Федерации, поэтому требования, предъявляемые к выбору проекций для построения карт России, можно примнить и для карт Казахстана. Карты Казахстана, а также территории отдельных его регионов преимущественно строят в нормальных конических проекциях. Наибольшее применение имели и имеют нормальные равнопромежуточные конические проекции, несколько реже нормальные равноугольные, а в последние годы, для построения электронных вариантов карт, и нормальные равновеликие конические проекции.Карты Казахстана используются в самых различных целях, в том числе и для решения картометрических задач. Поэтому искажения должны быть малыми. В связи с этим при создании карт Кахазстана и карт его отдельных регионов большое внимание уделяется выбору широт главных параллелей. Этот выбор делается так, чтобы минимизировать величины искажений в проекции.
Формулы нормальной равнопромежуточной по меридианам конических проекций, предлагаемых для построения карт Казахстана, частей его территории.
-------------------------------------------------------------------------------------------------------
22.Общая теория цилиндрических проекций. Равноугольные цилиндрические проекции. Виды цилиндрических проекций, их использование.
Цилиндрические
проекции.
Цилиндрическими
называют проекции, в которых меридианы
– равноотстоящие параллельные прямые,
а параллели- параллельные прямые,
ортогональные меридианам. Общие
уравнения этих проекций по определению
имеют вид:
,
Где
с – постоянный параметр. Записав
производные по ɸ и λ от этих общих
функций и подставив их значения в
формулы характеристик из общей теории
картографических проекций , получаем
в общем виде выражения для вычисления
частных масштабов длин и площадей, а
также наибольших искажений углов
,
где
а и b
– экстремальные частные масштабы длин.
Так как в этих проекциях картографическая
сетка ортогональна, то экстремальные
частные масштабы длин совпадают с
частными масштабами длин вдоль меридианов
и параллелей и вместо а и b
можно использовать значения n
и m.
Постоянный
параметр с проекции найдем из условия,
что на заданной параллели ɸ=
частный масштаб
=1,
тогда с=
.
Общие уравнения цилиндрических проекций принимают вид:
,
где а и b— экстремальные масштабы длин.
Из приведенных формул видно, что в этих проекциях частные масштабы и искажения явл-ся функциями только широты. Следовательно, в них линии равных искажений(изоколы) совпадают с парраллелями.
Цилиндрические проекции по характеру искажений делятся на равноуголльные, равновеликие и равнопромежуточные вдоль меридианов.
Равноугольные
цилиндрические проекции. При получении
равноугольных нормальных цилинрических
проекций должны выполняться условия
равноугольного отображения эллипсоида
на плоскости:
m=n;
ἐ=0.Так как в этих проекциях ἐ=0, то
подставив в первое условие значения
частных масштабов длин, получаем
дифференциальное уравнение
.
Поскольку проекция симметрична
относительно экватора, то на экваторе
при ɸ=0 и x=0,
отсюда и с=0. Формулы проекции эллипсоида
принимают вид
Равноугольная
цилиндрическая проекция шара была
предложена Меркатором в 1569 году. В
настоящее время равноугольные
цилиндрические проекции шара и эллипсоида
известны под названием проекций
Меркатора; они обладают свойством
локсодромичности, что определило их
широкое применение для составления
морских и аэронавигационных карт.
Локсодромией наз-ся линия, пересекающая
все меридианы под постоянным углом. В
равноугольных цилиндрических проекциях
локсодромии изображаются прямыми
линиями. При отображении поверхности
шара е=0 и формулы проекции Меркатора
можно записать в виде
Анализ формул проекции Меркатора позволяет отметить, что в проекции изменение масштабов медленнее всего происходит вблизи экватора, который является центральной линией цилиндрических проекций.
По характеру искажений цилиндрические проекции могут быть равноугольными, равновеликими и произвольными. Применяются прямые, косые и поперечные цилиндрические проекции в зависимости от расположения изображаемой области. В косых и поперечных проекциях меридианы и параллели изображаются различными кривыми, но средний меридиан проекции, на котором располагается полюс косой системы, всегда прямой.
---------------------------------------------------------------------------------------------------------