17. Поликонические проекции карт мира. Построение и использование нормальной квадратно-цилиндрической проекции.

Поликонические проекции для карт мира имеют наибольшее значение. Рассмотрим основные из них. Равноугольная проекция Лагранжа. По абсолютному значению искажения площадей умеренные, а для Африки и Северной Америки — большие. Однако для карты мира они приемлемы. Европа, Южная Америка и особенно Африка по площади преуменьшены, а Азия, Северная Америка и Австралии — преувеличены. В результате создается впечатление повышенного контраста в размерах этих объектов. Формы объектов искажены по-разному: у Африки небольшие искажения; умеренные искажения у Европы, Южной Америки и Австралии, большие — у Северной Америки и Азии. Это является следствием того, что радиусы кругов, обращенные к полюсам, изобразились значительно длиннее радиусов, направленных в сторону экватора. Вместе с этим проекция обладает довольно высокой степенью стереографичности: величины показателей искажений формы кругов колеблются в пределах от малых до умеренных значений. Проекцию Лагранжа следует использовать для карт мира в тех случаях, когда необходимо, чтобы текущие углы между линиями и направления линий тех или иных потоков передавались без искажений. В России для карт мира наибольшее значение имеют полико-нические проекции ЦНИИГАиК. Координаты узловых точек этих проекций и макеты карт с изоколами частных масштабов площадей и максимальных искажений углов даны в Атласе для выбора картографических проекций (1957). Кратко рассмотрим эти проекции. Поликоническая проекция ЦНИИГАиК (1939—1949) (Г.А.Гинзбурга). Долгота среднего меридиана +10°. Все параллели равноразделенные. Масштаб длин вдоль экватора равен 0,9, а вдоль среднего меридиана — 1. Искажения площадей и углов одного порядка. Наибольшие искажения углов не превышают 50°. Масштабы площадей изменяются от 0,9 (в центральной части) до 1,8 (на крайних выступах северного побережья) и до 2 и более (в полярных районах). Нет искажений всех видов на среднем меридиане в двух точках с широтами ±52°. Проекция использовалась для построения климатических и других физико-географических карт. Поликоническая проекция ЦНИИГАиК (1950). Долгота среднего меридиана +30°. Все параллели равноразделенные. Параллели изображаются дугами окружностей мень- шей кривизны, чем в предыдущем варианте. Главный масштаб длин сохраняется по среднему меридиану и по параллели ±48°. Площади искажены несколько меньше, чем углы. Наименьшее искажение площадей в центре карты, где частный масштаб площади равен р = 0,823. На северных окраинах материков р = 1,5 — 2, в полярных районах р немного превышает 2. Наибольшие искажения углов в приполярных областях у верхней и нижней рамок карты, где максимальные искажения углов со превышают 70е. Масштаб длин вдоль экватора равен 0,823. Отсутствуют искажения на среднем меридиане в двух точках с широтами ±48°. В этой проекции были построены Политическая карта мира, карты народов мира и плотности населения, а также многие карты мира в школьных атласах. Поликоническая проекция ЦНИИГАиК (1954) предназначена для настенных карт. Проекция составная. Макеты картографической сетки с изоколами частного масштаба площадей и наибольших искажений углов имеются на рис. 51, 52. Таблицы с координатами узловых точек приведены в Атласе для выбора картографических проекций (1957). На практике применяется видоизмененный вариант проекции. В видоизмененном варианте средний меридиан с долготой +5° (вместо +50°) на карте не приводится. Гринвичский меридиан зрительно воспринимается прямолинейным. Проекция перестала быть составной, так как использована только западная часть исходной проекции. Теперь картографическая сетка симметрична как относительно среднего меридиана, так и относительно экватора. Проекция большей частью обладает умеренными искажениями углов и площадей. По локальным оценкам, на суше искажения углов, исключая ее повторяющиеся части на карте, не превышают 30°. Масштаб площадей для значительной части суши изменяется от 0,83 до 1,5. В полярных районах р = 3,0 и более.. Квадрантно-цилиндрическая проекция. Рассмотрим построение сетки простой цилиндрической или квадратноцилиндрической проекции - самой простиой не только среди цилиндрических, но и среди всех картографических проекций. Обозначим через R0 радиус глобуса, разность широт - Δφ , разность долгот - Δλ, тогда расстояния Δφ между параллелями и расстояние Δλ между меридианами будут равны: (1) Δx=R0·Δφ0/ρ0 (2) Δy= R0·Δωλ0/ρ0 , где ρ0 = 57029578 – число градусов в одном радиане. Отсюда видно, что приравенстве широт и долгот, т.е. при Δφ=Δλ должно быть и Δx=Δy Для вычисления по этим формулам необходимо знать радиус глобуса R0 . Он равен R0 =μ0·R, где μ0 – главный (заданный) масштаб карты, R – радиус Земли. (Здесь надо иметьв виду, что μ0 не знаменатель, а сам масштаб). Теперь поставив значение R0 в верхние формулы (1) и (2) и выражая Δx и Δy в сантиметрах (для чего правые части умножаем на 100, если радиус задан в метрах или на 1000, если он задан в километрах), получим окончательные формулы для вычисления сетки в простой цилиндрической проекции: (3) Δx=100·μ0· R· Δφ0/ρ0 (или 1000· μ0· R· Δφ0/ρ0) (4) Δy= 100·μ0·R· Δωλ0/ρ0 (или 1000· μ0·R· Δωλ0/ρ0) Для практического применения этих формул в конкретном случае необходимо указать: 1. числовые значения главного масштаба μ0 2. величину Δφ=Δλ (частоту сетки) 3. радиус земного шара (обычно для упрощения берут R= 6370 км, но можно взять радиус земного шара одинаковой поверхности с поверхностью эллипсоида Красовского, т.е. R= 6371,116 км, или R= 6371116 м) В этой проекции эллипс искажений по мере удаления от экватора все более и более вытягивается вдоль параллели, превращаясь на полюсах в линию. Здесь же на полюсах максимальные искажения ω достигают 1800. Вот почему эта проекция наиболее удобна для изображения экваториальных стран и для составления зодиакальных карт неба. В целях уменьшения крайних искажений вместо касательного цилиндра можно взять секуший цилиндр с параллелями сечения ±φ0 , отстоящими от экватора на равных расстояниях. В этой проекции, известной в древности (около 100 лет до н.э. – Марин Тирский), расстояния между двумя смежными меридианами на карте равны выпрямленной дуге параллели сечения между теми же меридианами на глобусе, а расстояния между параллелями на карте равны выпрямленным дугам меридиана – как и в квадратной проекции.

--------------------------------------------------------------------------------------------------------

18. Формулы, используемые для построения нормальной равновеликой азимутальной проекции шара. Равновеликая азимутальная проекция. Немецкий математик Ламберт еще в 1772 г. разработал эту проекцию. В ней концентрические окружности, изображающие параллели нормальной сетки, проводятся радиусами, равными хордам АР параллели АВ на глобусе, т.е. АР = ρ = 2R·sinℓ/2 . При таком построении параллелей сохраняются площади на карте. Доказательство: Площадь круга на карте радиуса АР = ρ равна S=π(AP)2. Из геометрии известно, что площадь сегмента АРВ шаре равна произведению длины окружности большого круга на высоту сегмента – РО: Sсег.=2πR·PO. Из ΔР1АР можно написать, что катет АР=ρ есть среднее пропорциональное между гипотенузой и прилежащим отрезком РО. РО/АР = АР/2R . Откуда АР2= 2R· РО. Подставив последнее выражение в формулу сегмента Sсег.=π(АР)2 получим Sсег.=2πR·PO, что и требовалось доказать. Равновеликая азимутальная проекция Ламберта является частным случаем равновеликой конической проекции. Формулу для радиусов параллелей можно также вывести на основании общих формул азимутальных проекций, подставив условие равновеликости m·n=1, при μ=1: - dρ/R·dφ · ρ/R·cosφ = 1. Интегрируя выражение, получим: φ ρ2/2 = - R2 ∫ cosφ·dφ = R2(1-sinφ) или, выражая угол φ через полярное расстояние ℓ= π/2-φ π/2 получим: ρ2=2R2(1-cosφ) = 4R2·sin2ℓ/2. Откуда ρ = R √2(1-cosℓ) = 2R·sinℓ/2. Увеличение m вдоль меридианов находят: m= cos ℓ/2 Увеличение n параллелям находят: n= sec ℓ/2. Увеличение p найдем исходя из: p=m·n = cosφ·secφ= cosφ· 1/cosφ = 1. Наибольшее искажение углов можно вычислить по формуле: tg(450+ω/4)= secℓ/4.

Карты Северного и Южного полушарий обычно строят в нормальной равнопромежуточной азимутальной проекции. Макет карты Северного полушария дан на рис. (строим рисунок: круг делим на 36 равных частей. Возьми циркуль, транспортир), а Южного полушария —(то же самое, толькое южное полушарие).

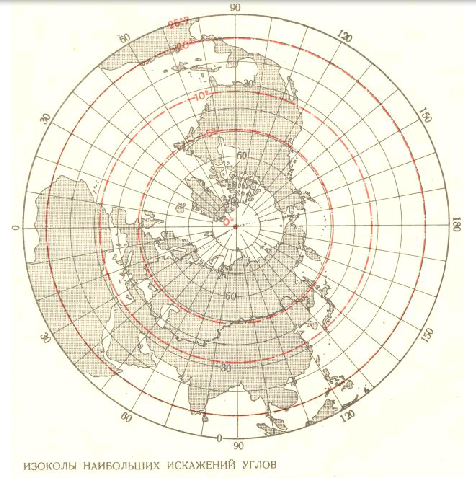
Рис. Изоколы площадей (1) и изоколы наибольших искажений углов (2)

1. Частный масштаб длин по параллелям изменяется от 1 (на полюсах) до 1,571 (на экваторе). Полушария ограничены экватором. Максимальные искажения углов имеют место на экваторе и приближаются к 26˚. 1. На карте полушарий нет искажений всех видов в центральной точке, совпадающей с северным полюсом. 2. По характеру искажений проекция относится к равнопромежуточным проекциям. В пределах карты значения (р-1) изменяются от 0% в центральной точке полюса до +57% на периферии, а значения w , соответственно, от 0° до 25°,7. 3. Проекцию следует применять для карт северного полушария, на которых искажения площадей и углов должны быть одного порядка и требуется сохранить длины вдоль всех меридианов. 4. Проекция может применяться также для карт южного полушария и для карт звёздных полушарий.

---------------------------------------------------------------------------------------------------------