15. Проекции, показывающие сферичность полушарий Земли.

Для придания полушариям эффекта сферичности чаще других применяют азимутальную ортографическую проекцию. Ее строят в поперечной или в косой ориентировке. При этом на карте полушария планет получаются такими, какими наблюдатель видит их в действительности с очень больших расстояний. В ортографической проекции по материалам телескопических наблюдений были построены некоторые карты Луны и планет.

В зависимости от компоновки карты могут выбираться различные значения координат центральной точки.

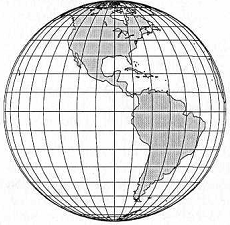
Рис. Поперечная и косая ортографическая азимутальная проекции

Существенным недостатком азимутальной ортографической проекции является то, что ей присущи очень большие искажения всех видов. Например, даже в центральной части карты искажения углов около 10°, а искажения площадей — около 10%.

При зенитном расстоянии 40° площади искажены более чем на 20 %. При зенитном расстоянии 60° изображение практически не читается. На карте полушарий в ортографической проекции искажения площадей изменяются от 0 (в центре карты) до -100% (на краях полушария). Искажения углов соответственно изменяются от 0 до 180°.

Развитие космической фотосъемки побудило к использованию перспективных внешних азимутальных проекций, которые геометрически строятся по тем же правилам, что и космофотоснимки.

Например, в косой внешней перспективной проекции составлена карта видимого полушария Луны масштаба 1: 5 000 000. Однако чем с больших расстояний выполнена фотосъемка, тем ближе

перспективная внешняя азимутальная проекция к ортографической. По показателям искажений она также очень близка к ортографической проекции и имеет те же недостатки.

Сферичностью обладает также ортографическая двойного проектирования проекция Гильберта. Земной шар спроектирован при условии равноугольности на полусферу, которая затем ортографически была отображена на плоскости.

---------------------------------------------------------------------------------------------------------

16. Распознавание картографических проекций. Определение проекции и ее данных по карте. Карты Казахстана в нормальной равноугольной конической проекции.

Пользователю картографической продукции важно знать проекцию, чтобы иметь представление о свойствах и возможностях использования интересующей его карты. Составителям эти сведения еще более необходимы, чтобы судить о возможности ее применения в качестве исходного картографического материала при создании новой карты. Определить картографическую проекцию – это в современных условиях означает выяснить элементы и параметры ее математической и геодезической основ. Для геоинформационного картографирования недостаточно установить название проекции, мало знать о ее принадлежности к определенной группе или классу. Для качественного перевода изображения карты в цифровую форму и для осуществления обработки и преобразования данных важно также располагать уравнениями проекции, параметрами этих уравнений, а также параметрами использованной геодезической основы. Пути распознавания проекции: • Знакомство с данными о проекции на полях карты или с прилагаемой к ней документации. В условиях геоинформационных технологий эта информация должна входить в состав метаданных или включаться в паспорт карты. • Изучение особенностей ее картографической сетки (вида меридианов и параллелей, величины углов пересечения координатных линий, изменения длин дуг меридианов с широтой и изменения длин дуг параллелей с долготой, наличие и положение и характер среднего меридиана). Этот путь наиболее эффективен для распознавания проекций карт большого территориального охвата. На основе всех выявленных особенностей можно составить специальную таблицу. • Определение по карте частных масштабов длин, площадей, углов и по ним определить класс проекции по видам картографических искажений. • Изучение литературных источников - учебников, учебных и учебно-справочных пособий, научных статей, монографий, атласов для выбора картографических проекций. Нормальные равноугольные конические проекции обычно применяются для построения в сравнительно крупных масштабах карт частей Российской Федерации(для КЗ – тоже пайдет)). В атласах в этой проекции даются карты, например, регионов европейской части России, Урала, Поволжья, Западной Сибири, Восточной Сибири, Дальнего Востока. Координаты точек в проекции вычисляются по таким же формулам, как и для нормальной равнопромежуточной конической проекции, за исключением радиусов параллелей, которые определяются по формуле ρ = Се¯ª ⁿ = CU¯ª, где n — изометрическая широта; U — функция, связанная с изометрической широтой. Чаще всего применяется секущий конус и способы Витковского или Каврайского для нахождения широт двух главных параллелей и вычисления параметров проекции а, С. Если широты главных параллелей определены, то параметры вычисляются по формулам: α = (lnr1-lnr2)/(lnU2-lnU1) ; C = r1U1ª / α = r2U2 ª / α. Наиболее строгий способ расчета параметров, как и для равнопромежуточных проекций, основан на минимизации взвешенной суммы квадратов искажений (n-1) частных масштабов длин на параллелях. С учетом выражения для частного масштаба длин n в равноугольной проекции минимизируемая функция принимает следующий вид: Σ(kg/Σkg)((αC/rUª)-1)² = min, где а и С — искомые параметры проекции; г — радиус текущей параллели; g — геометрический вес; к — экономический весовой коэффициент (в частном случае принимается к = 1).

--------------------------------------------------------------------------------------------------------