38.Автомат з магазинною пам’яттю

Автома́т з магази́нною па́м'яттю (МП автомат) — в теорії автоматів це скінченний автомат, що використовує стек для зберігання станів.На відміну від скінченних автоматів, автомат з магазинною пам'яттю є набором , де

• K — скінченна множина станів автомата

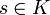•  — єдиний допустимий початковий стан автомата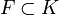

•  — множина кінцевих станів, причому допускається F=Ø, і F=K

• Σ — скінченна множина символів вхідного алфавіту, з якого формуються строки, що зчитуються автоматом

• S — алфавіт пам'яті (магазину)

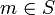•  — нульовий символ пам'яті.

Пам'ять працює як стек, тобто для читання доступний останній записаний в неї елемент. Таким чином, функція переходу є відображенням  . Тобто, по комбінації поточного стану, вхідного символу і символу на вершині магазину автомат вибирає наступний стан і, можливо, символ для запису в магазин. У випадку, коли у правій частині автоматного правила присутній  , в магазин нічого не додається, а елемент з вершини стирається. Якщо магазин порожній, то спрацьовують правила з   в лівій частині.

Автомат з магазинної пам'яттю може розпізнати будь-яку контекстно-вільну мову.

У чистому вигляді автомати з магазинною пам'яттю використовуються вкрай рідко. Зазвичай ця модель використовується для наочного подання відмінності звичайних скінченних автоматів від синтаксичних граматик. Реалізація автоматів з магазинною пам'яттю відрізняється від кінцевих автоматів тим, що поточний стан автомата сильно залежить від будь-якого попереднього.

Види автоматів з магазинної пам'яттю

Існують детерміновані та недетерміновані автомати з магазинною пам'яттю. Для недетермінованих автоматів (на відміну від детермінованих) існує два еквівалентні критерії завершення роботи:

• порожній магазин

• досягнення кінцевого стану

Детермінований автомат завершує роботу лише тоді, коли досягає кінцевого стану.

37.Скінче́нний автома́т, є особливим видом автомату — абстракції, що використовується для описання шляху зміни стану об'єкта в залежності від досягнутого стану та інформації отриманої ззовні. Його особливістю є скінченність множини станів автомату. Поняття скінченного автомата було запропоновано в якості математичної моделі технічних приладів дискретної дії, оскільки будь який такий пристрій (в силу скінченності своїх розмірів) може мати тільки скінченну кількість станів.

Скінченні автомати можуть розв'язувати велику кількість задач, серед яких автоматизація проектування електронних приладів, проектування комунікаційних протоколів, синтаксичний аналіз та інші інженерні застосування. В біології і дослідженнях штучного інтелекту, автомати або їх ієрархії іноді використовуються для описання неврологічних систем і в лінгвістицідля описання граматики природніх мов.

Класифікація

Існує дві різних групи автоматів: Акцептори/Розпізнавачі і Перетворювачі(Трансдуктори).

Акцептори і розпізнавачі

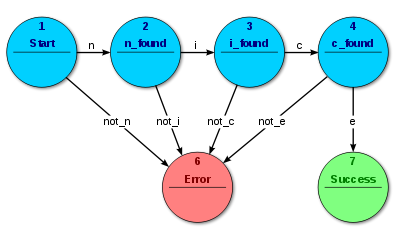
СА акцептор: виконує розбір слова "nice"

Акцептори і розпізнавачі (також виявлювачі послідовностей) продукують двійковий вихід, кажучи або такабо ні на питання прийняті автоматом вхідні дані чи ні. Всі стани СА можуть бути або допустими або ні. Коли всі вхідні дані оброблені, якщо поточний стан є допустимим, значить вхід прийнятий; інакше відхилений. Як правило на вхід подаються символи (літери); дії не використовуються. Приклад на зображенні показує СА який приймає слово «nice». В цьому СА єдиний допустимий стан це 7.

Автомат також може бути описаний як такий, що визначає мову, яка містить всі слова розпізнавані цим автоматом, але не ті які ним відхиляються; тоді ми кажемо, що ця мова розпізнається автоматом. За визначенням, мови розпізнавані СА це регулярні мови тобто мова є регулярною якщо існує деякий СА, який розпізнає її.

.

36. Розпізнавані

Розпізнавай, припустимий рядок, визначена розпізнавачем мова

Автомати, що використовуються для визначення мови, частіше є тими, що розпізнають, їх називають розпізнавачами. За допомогою розпізнавачів, також як і за допомогою граматик, можна од­нозначно визначити мову.

Звичайно припускається, що вхідна голівка розпізнавача тільки читає.

Розглянемо деякий рядок (о. Розпізнавач допускає вхід­ний рядок (0, якщо, починаючи з початкової конфігурації, в якій рядок со записаний на вхідній стрічці, розпізнавач може зробити послідовність кроків, що закінчується завершальною конфігурацією. Слід вказати, що, починаючи з даної початко­вої конфігурації недетермінований розпізнавач може виконати багато різних послідовностей кроків. Якщо хоча б одна з цих послідовностей закінчується завершальною конфігурацією, то початковий вхідний ланцюжок буде допущений.

Мова, що визначена розпізнаване м, зображує множину вхідних ланцюжків, які вона допускає.

Для кожного класу граматик з ієрархії Хомського існує клас розпізнавачів, що визначає той же клас мов. Цими розпізнава­чами є скінченні автомати, автомати з магазинною пам'яттю, лінійно обмежені автомати та машини Тьюринга. Точніше мови з ієрархії Хомського можна охарактеризувати так:

1. Мова регулярна (праволінійна або ліволінійна) тоді і тіль­ки тоді, коли вона визначається скінченним автоматом.

2. Мова контекстно-вільна тоді і тільки тоді, коли вона ви­значається автоматом з магазинною пам'яттю.

3. Мова контекстно-залежна тоді і тільки тоді, коли вона ви­значається лінійно обмеженим автоматом.

4. Мова визначається граматикою загального виду тоді і тіль­ки тоді, коли вона визначається машиною Тьюринга.

Всі наведені чотири типи автоматів описуються у наступ­них розділах

32.Дерева виводів.

Дерево виводу. Стратегії виводу: зверху вниз, зліва направо, знизу вверх

В граматиці може бути кілька виводів, що еквівалентні

у тому значенні, що в кожному виводі застосовуються одні й ті ж продукції в одних і тих же місцях, але у різному порядку. Визначити поняття еквівалентності двох виводів для граматик довільного виду складно, але у випадку КВ-граматик можна ввести зручне графічне зображення класу еквівалентних виво­дів, що називається деревом виводу.

Визначення

Позначене упорядковане дерево В називається деревом ви­воду (або деревом розбору) у КВ-граматиці G = (N,T,P,S), якщо виконані такі умови:

1. Корінь дерева D позначений S, а кожна вершина дере­ва D — символом з N ᴗ Т ᴗ {ε }.

2. Для будь-якої внутрішньої вершини Х₀ дерева і упоряд­кованого списку її синів Хі, Х₂, Х_п множина продукцій граматики Р включає таку продукцію А —> а₁ а₂, ..., а_n, що А, а₁ а₂, ..., а_n є позначками вершин Х₀, Хі, Х₂, ..., Х„ відповідно.

3. Якщо корінь дерева має єдиного нащадка, що позна­чений є, то цей нащадок домінує над деревом, яке скла­дається з єдиної вершини ε, і S —» ε — продукція з мно­жини Р.

На рис. 7.2 зображено дерева виводів у граматиці G з продукціями S -> aSbS|bSaS| ε.

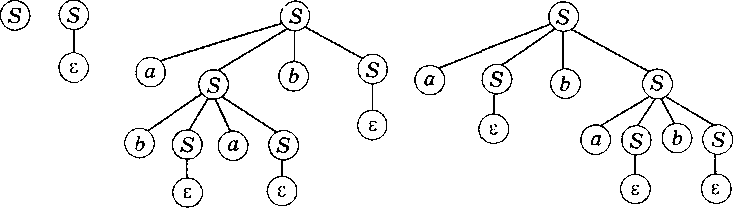
Рис. 7.2. Дерева виводів у граматиці з

продукціями продукціями S -> aSbS|bSaS|ε

33.Стратегії виводів

При граматичному розборі порядок заповнення дерева зводиться до однієї з двох стратегій: зверху вниз (рис. 7.4,а) і знизу вверх (рис. 7.4,в). При заповненні зверху вниз — стра­тегія спадного аналізу — всі попередники кожної заповню­ваної у дереві внутрішньої вершини до даного моменту вже заповнені.

Заповнення знизу вверх — стратегія східного аналізу — характеризується тим, що всі спадкоємці кожної заповнюваної у дереві вершини вже належать побудованій частині дерева. Таким чином, при заповненні дерева зверху вниз рухання здійснюється від його кореня до висячих вер­шин, а при заповненні знизу вверх — навпаки.

При заповнен­ні зліва направо — стратегія горизонтального аналізу— на кожному кроці відбувається заміна самого лівого нетермінального символу термінальним.

29.Форма  Бе́куса—Нау́ра (англ. Backus-Naur form, BNF) — це спосіб запису правил контекстно-вільної граматики, себто формою опису формальної мови.

Саме її типово використовують для запису правил мов програмування та протоколів комунікації. У 50-х роках минулого сторіччяДжон Бекус створив цю нотацію розробляючи мову ALGOL. На першому Всесвітньому Комп'ютерному Конгресі, що відбувся уПарижі 1959-го він зробив доповідь на тему «Синтаксис та семантика пропонованої першої міжнародної алгебраїчної мови». Пізніше Наур Пітер спростив її та (за порадою Дональда Кнута) додав до назви своє ім'я.

Вона особливо корисна, коли ми викори­стовуємо елементи з N, які можна переплутати з елементами з Т. Ця нотація полягає у такому:

1. Символ >» заміняється на «::=».

2. В кутові дужки «< >» беруться нетермінальні сим­воли.

3. Знак «|» використовується для скороченого запису про­дукцій, позначає «або» і об'єднує групу продукцій з однаковою лівою частиною, але різними правими частинами.