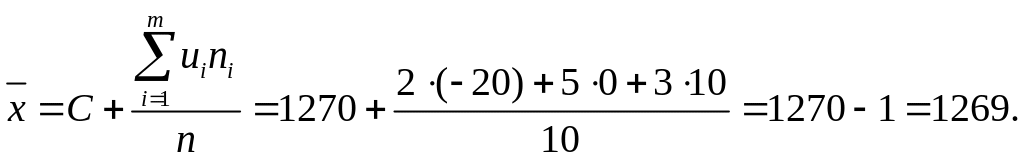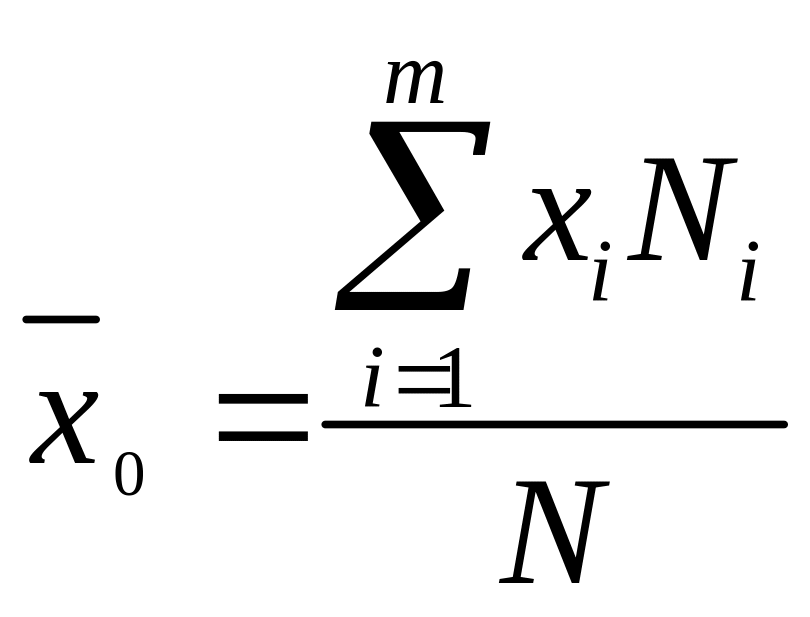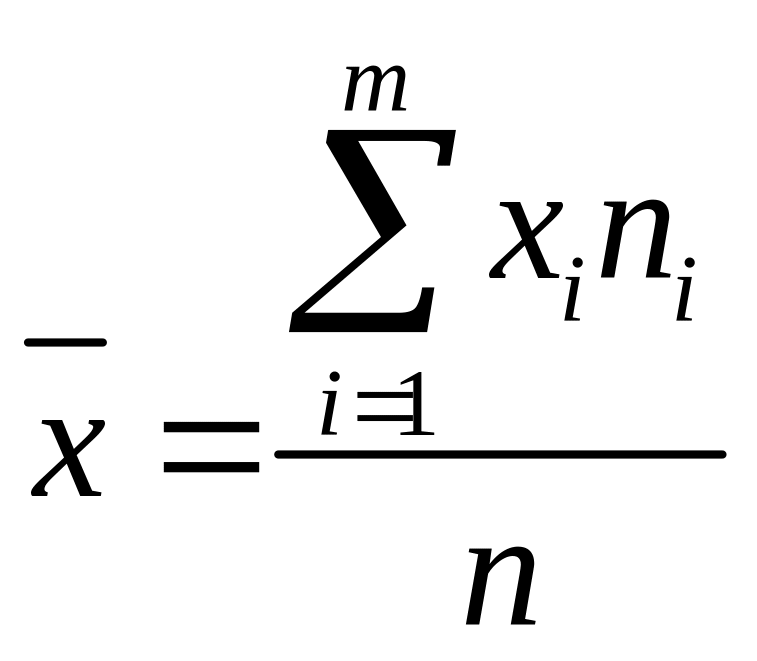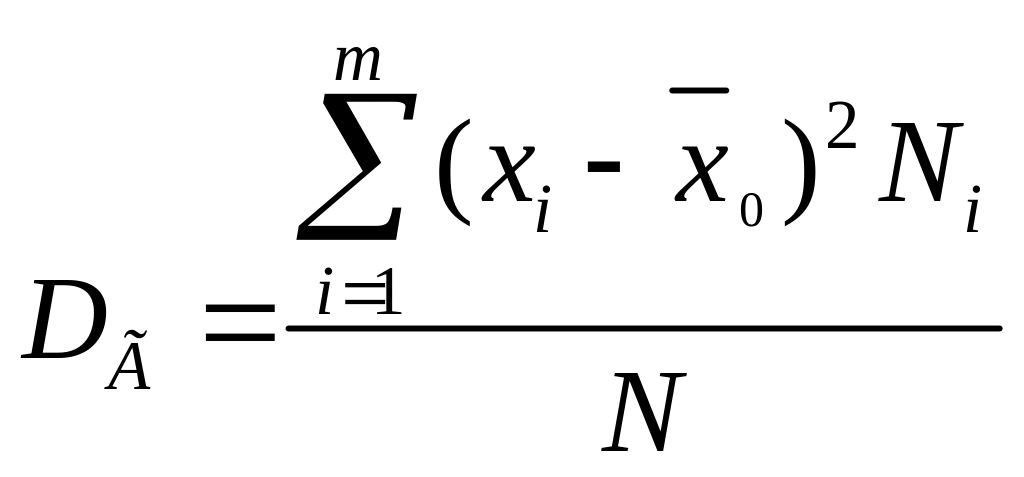3.5.4. Понятие оценки параметров

Математическая теория выборочного метода основана на анализе собственно-случайной выборки. Введем некоторые обозначения:

– значения признака (случайной величины );

и – объемы генеральной и выборочной совокупностей;

и – число элементов генеральной и выборочной совокупностей со значением признака ;

и – число элементов генеральной и выборочной совокупностей, обладающих данным признаком.

Средние арифметические распределения признака в генеральной и выборочной совокупностях называются соответственно генеральной и выборочной средними, а дисперсии этих распределений – генеральной и выборочной дисперсиями.

Отношения и называются соответственно генеральной и выборочной долями.

Все формулы сведем в таблицу

Наименование характеристики	Генеральная совокупность	Выборка
Средняя
Дисперсия
Доля

Задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.

Пусть распределение признака – генеральной совокупности – задается функцией вероятностей для дискретной случайной величины или плотностью вероятности для непрерывной случайной величины, которые содержат неизвестный параметр . Например, это параметр в распределении Пуассона или параметры или для нормального распределения и т. д.

Для вычисления параметра использовать генеральную совокупность не предоставляется возможности. Поэтому о параметре судят по выборке, состоящей из значений (вариантов) . Эти значения можно рассматривать как частные значения независимых случайных величин , каждая из котрых имеет тот же закон распределения, что сама случайная величина .

Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Точечной называют статистическую оценку, которая определяется числом , где – результаты наблюдений над количественным признаком ( выборка).

Точечная оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки: .

Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя:

,

где – варианта выборки, – частота варианты , – объем выборки.

Если первоначальные варианты – большие числа, то для упрощения вычислений целесообразно вычесть из каждой варианты одно и то же число , то есть перейти к условным вариантам (в качестве выгодно взять число, близкое к выборочной средней; но так как выборочная средняя неизвестна, то число выбирают наугад). Тогда

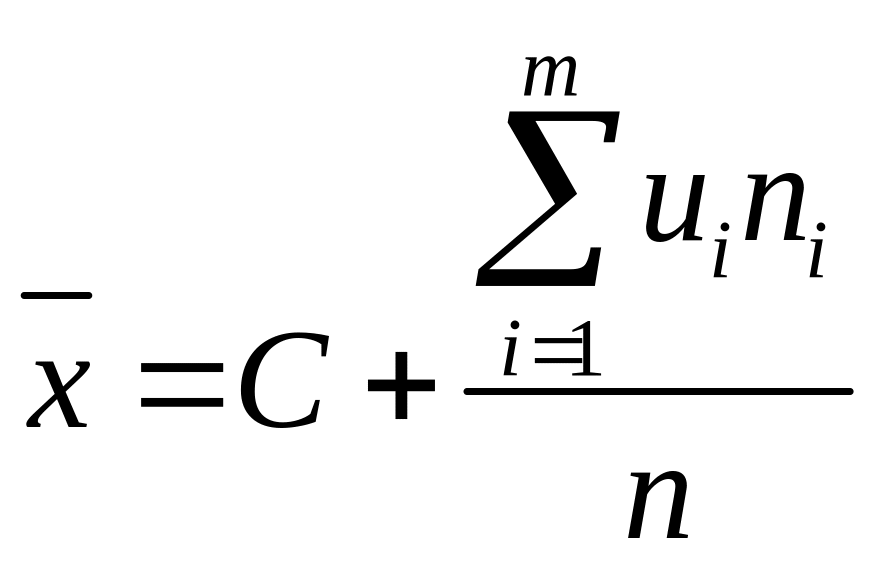
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:

.

Эта оценка является смещенной, так как

.

Более удобна формула

.

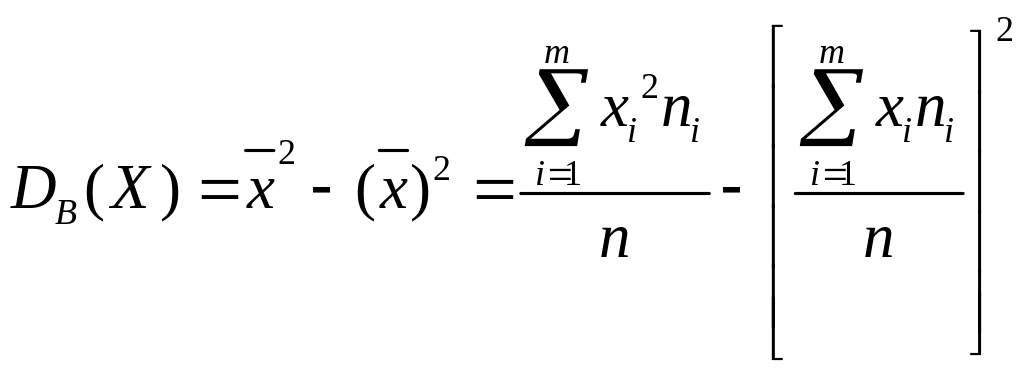Если первоначальные варианты – большие числа, то следует перейти к условным вариантам (дисперсия при этом не изменится). Тогда

.

Если первоначальные варианты являются десятичными дробями с десятичными знаками после запятой, то переходят к условным вариантам , где . При этом дисперсия увеличивается в раз. Поэтому

.

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

.

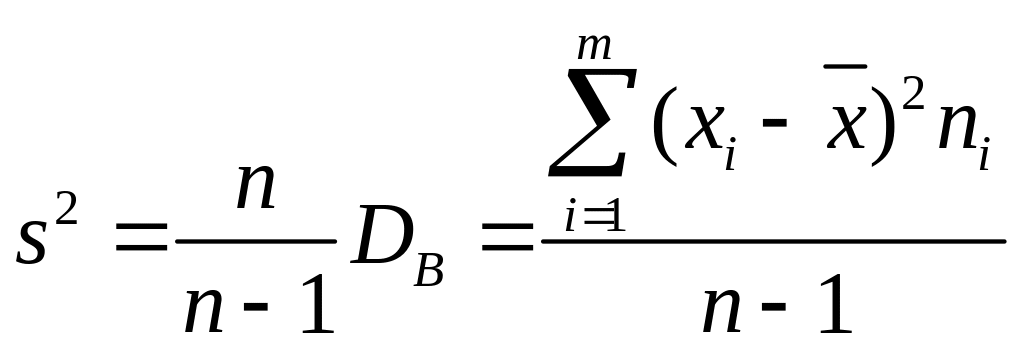Более удобна формула

.

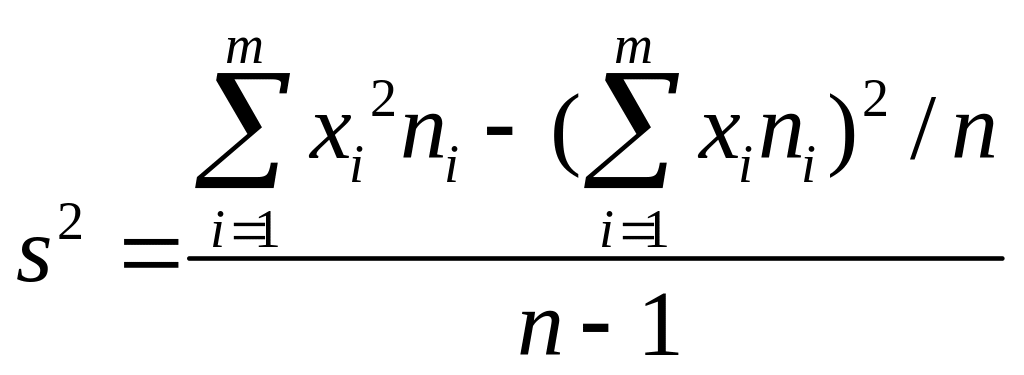В условных вариантах она имеет вид

,

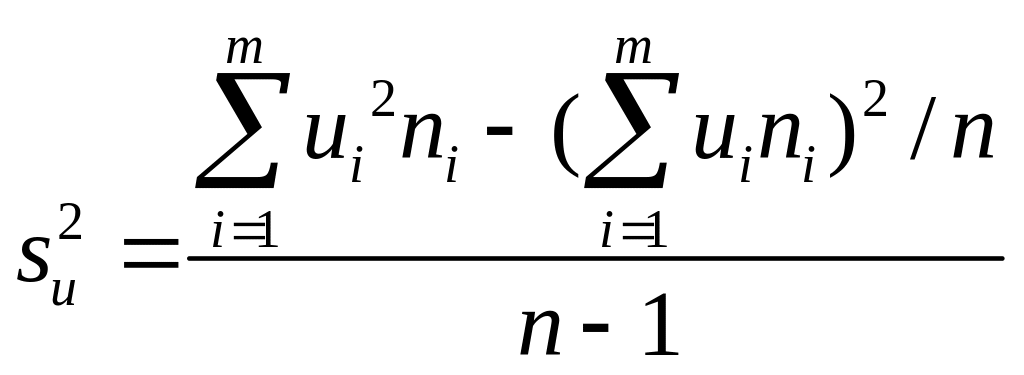причем, если , то , а если , .

23. Из генеральной совокупности извлечена выборка объема :

варианта 2 5 7 10

частота 16 12 8 14

Найдите несмещенную оценку генеральной средней.

Решение. Несмещенной оценкой генеральной средней служит выборочная средняя:

.

Поэтому =16.

24. Из генеральной совокупности извлечена выборка объема :

варианта 1 3 6 26

частота 8 40 10 2

Найдите несмещенную оценку генеральной средней.

25. Найдите выборочную среднюю по данному распределению выборки объема : варианта 1250 1270 1280

частота 2 5 3

Решение. Первоначальные варианты – большие числа, поэтому перейдем к условным вариантам . В результате получим:

варианта 20 0 10

частота 2 5 3

Найдем искомую выборочную среднюю: