148. Найдите мощность множества точек: а) параболы; б) гиперболы;
149. Покажите равномощность множества точек прямой и множества точек интервала (0, 1).
Решение.
Д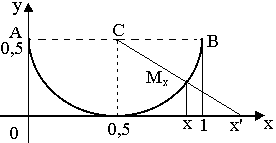
ля
того, чтобы показать равномощность
интервала и прямой, необходимо установить
между ними биекцию. На координатной
плоскости рассмотрим полуокружность
с радиусом 0,5 и центром в точке С (0,5;0,5)
(см. рис.) и прямую, касательную к окружности
в точке (0,5; 0), – ось Ох. Каждую точку х
из интервала (0,1) проектируем на
полуокружность по направлению
перпендикуляра к прямой Ох в точку Мх.
Затем из центра С окружности проводим
луч через точку Mx.
до пересечения с осью Ох в точке x'. Таким
образом, каждой точке интервала ставится
в соответствие точка на оси Ох. Пусть
теперь точка х интервала рассматривается
как точка прямой. Посмотрим, какая точка
ей отвечает на интервале. Для нахождения
этой точки проведем прямую хС и найдем
пересечение ее с полуокружностью. Пусть
это будет точка К. Опустим перпендикуляр
из точки К на ось Ох. Он пересечет Ох в
точке х1.В
построенном выше отображении х1
перейдет
в точку х. Таким образом, соответствие,
при котором точке х интервала (0, 1)
ставится в соответствие точка x' оси Ох,
является биективным. Задача решена.
150. Докажите равномощность множества точек луча [0, +¥) и множества точек промежутка [0, 1).
Указание. Используйте метод, которым решена предыдущая задача.
151. Докажите, что окружность и интервал равномощны.
152.
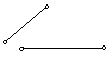У
становите
биекцию между отрезками:
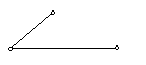1)
2)
3)
153. Найдите взаимно однозначное отображение отрезка [0, 1] на отрезок [а, b].
154. Постройте взаимно однозначное отображение отрезка [0, 1] на интервал (0, 1).
Решение. Выделим
на интервале (0, 1) какую-либо последовательность
попарно различных точек, например: х1
=
,
х2
=
,
…, хn
=
,
… . Установим следующее соответствие:
точке 0 отрезка [0, 1] ставим в соответствие
точку х1
интервала (0, 1), точке 1 Î
[0, 1] – точку х2
Î
(0, 1), точке х1
=
Î
[0, 1] – точку х3
=
,
и вообще, точке хn
Î
[0, 1] – точку хn
+ 2 , то есть
точке
ставим в соответствие точку
.
Любую другую точку х Î
[0, 1], не задаваемую числом вида
,
отображаем на интервал в точку, задаваемую
тем же числом, что и отображаемая точка.
Полученное соответствие, очевидно,
является биективным.
155. Постройте биективное отображение окружности единичного радиуса на:
а) промежуток [0, 2p); б) на отрезок [0, 1].
156. Постройте какую-нибудь биекцию между следующими отрезками:
1) [A, B], [А,C]; 2) [A, B], [C, D].
157. Определите, каким множеством (конечным, счетным или множеством мощности континуум) является каждое из следующих множеств. Ответ обоснуйте.
1)
;
2)
;
3)
;
4)
;
5) A=Q;
6)
;
7)
;
8)
;
9)
.
10) Множество всех непересекающихся окружностей на плоскости;
11) Множество всех иррациональных чисел;
12) Множество всех точек отрезка [0; 1];
13) Множество всех десятичных дробей;
14) Множество всех вещественных чисел, заключённых между 0 и 1, в десятичной записи которых имеется цифра 7;
15) Множество всех рациональных чисел отрезка [a; b];
16) Множество всех пар натуральных чисел;
17) Множество всех пар рациональных чисел;
18) Множество всех точек графика функции: а) y = tgx, б) y = log2x;
19) Множество всех точек квадрата;
20) Множество всех точек плоскости, лежащих на осях координат;
21) Множество всех
чисел вида
где
