7. Тиімді (эффективной) және кесімді (номинальная) мөлшерлеменің айырмашылығы неде? Мысалдар келтіріңіз.

Кесімді мөлшерлеме

Күрделі пайыздық мөлшерлемелерді практикада беру үшін номинальді (кесімді) пайыздық мөлшерлемелер қолданылады. Оның мағнасы келесіде.

Егер сіз банкке ақша салсалсаңыз, онда пайыздар үзіліссіз есептеледі (начисляется), ал қандай да бір периодтылықпен – жылына, тоқсанына (квартал), айына тіпті күніне бір рет. Пайыздық ақшалардың осындай есептелу процессі және олардық салынған сомаға қосылуы «пайыздардың капитализациясы» деп аталады. Пайыздардың капитализациясы жылына m рет болсын делік. Егер j - номинальді пайыздық мөлшереме белгілі болса, онда пайыздардың әрбір есептелу кезінде салушының шотындағы сома 1+j/m рет өседі.

Мысал

Салушы банктегі шотқа 200 мың теңге салды. Егер номинальді пайыздық мөлшерлеме 8%-ға тең болса, ал пайыздар тоқсанына бір рет капитализацияланса (банк күрделі пайыздарды қолданады), онда жарты жылдан кейін оның шотындағы сомасы келесідей болады.

200 000 * (1 + 0,08/4)² = 208 080 теңге

Эффективті мөлшерлеме

Егер номинальді пайыздық мөлшерлеме берілсе және пайыздардың капитализациясы жылына рет болса, онда бір жылда салынған ақша (1+j /m )^m рет өседі.

Әрқашан күрделі пайыздық мөлшерлеме үшін қатынас орындалу керек болған үшін

i = (1 + j/m)^m – 1

Осылайша табылған күрделі пайыздық мөлшерлеме «тиімді» деп аталады, себебі ол номинальді мөлшерлемеге қарағанда, қазіргі қарыздық (ссудный) операцияның пайдалылығын сипаттайды.

Мысал

Егер номинальді мөлшерлеме 18%-ға тең болса және пайыздар ай сайын есептелсе, онда тиімді пайыздық мөлшерлеме келесідей болады

i = (1 + 0.18/12)¹² – 1 =0.1956 = 19.56%

Тиімді пайыздақ мөлшерлеме номинальдіге қарағанда әрқашан көп болады.

8. Жай және күрделі пайыздардың айырмашылығы? Мысалдар келтіру.

Жай пайыз бастапқы соманың негізінде есептеледі. Жай пайыз келесі формула бойынша есептеледі.

FV = PV(1+r*t)

FV (future value) – болашық құн

PV (present value) – ағымдағы құн

r – пайыздық мөлшерлеме

t - қаражаттың инвестицияланатын уақыт периоды

Күрделі пайыз алынған соманың қайта қаржыландыруын (рефинансирование) ескеру керек болған кезде қолданылады. Күрделі пайыз келесі формула бойынша есептеледі.

FV = PV(1+r)^t

Мысалы, қаражат 18 айға инвестицияланады. Бірдей пайыздық мөлшерлемемен күрделе пайызбен қаржы салу көбірек пайда алып келеді. Күрделі пайызбен қаржыны бірнеше жылға салғанда пайда белгілі бір програссиямен өседі.

Енді осыны көрейік:

Жай пайыз: FV = 1000*(1+0,1*1,5) = 1150

Күрделі пайыз: FV = 1000*(1+0,1/12)¹⁸ = 1161,112

Сонымен, қорта келгенде, жай пайыз пайыздық мөлшерлеме өлшемінде бастапқы сомаға есептеледі (начисляется), ал пайда алынған бойда алынады. Күрделі пайыз белгілі бір интервалдардан кейін алынатын пайда алынбай, бастапқы сомаға қосылғанда, қайта қаржыландыруды ұйғарады. Күрделі пайызбен алынатын пайда, жай пайызбен алынатын пайдадан көп болады.

9.Капитализациямен есептеу дегеніміз не? Мысалдар келтіру.

Пайыздар капитализациясы – бастапқы үлес сомасына пайыздарды қосып санау, яғни процент үстіне проценттің жүруі. Егер сіз банкке ақша салсалсаңыз, онда пайыздар үзіліссіз есептеледі (начисляется), ол қандай да бір периодтылықпен – жылына, тоқсанына (квартал), айына тіпті күніне бір рет. Пайыздық ақшалардың осындай есептелу процессі және олардың салынған сомаға қосылуы «пайыздардың капитализациясы» деп аталады. Пайыздардың капитализациясы жылына m рет болсын делік. Егер j - номинальді пайыздық мөлшереме белгілі болса, онда пайыздардың әрбір есептелу кезінде салушының шотындағы сома 1+j/m рет өседі.

Бұл күрделі процент формуласымен есептеледі FV=PV(1+r)^t . Бұл жерде PV (present value) – бастапқы салынған ақша, FV(future value) – болашақта алатын, процент қосылған ақшамыз. t – берілетін уақыт , r – проценттік мөлшерлеме.

Мысалы. Салушы банктегі шотқа 100 мың теңге салды. Егер номинальді пайыздық мөлшерлеме 11%-ға тең болса, ал пайыздар жылына бір рет капитализацияланса (банк күрделі пайыздарды қолданады), онда 10 айдан кейін оның шотындағы сома мынадай болады.

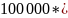=109 554 теңге