Пример.

а) Найти ФСР соответствующего однородного уравнения, то есть .

Характеристическое уравнение: ,

ФСР: ,

б) Записываем общее решение соответствующего однородного уравнения:

в) Найти какое-нибудь частное решение неоднородного уравнения методом вариации постоянное, то есть:

Пишем систему уравнений для производных C'_i:

Замечание. Поскольку при выводе метода вариации постоянных нигде не использовалось постоянство коэффициентов, то этот метод нахождения частного решения неоднородного уравнения полностью применим, когда коэффициенты уравнения a₀, a₁, …, a_n являются функции x.

Пример.

Соответствующее однородное уравнение:

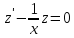
Мы получили общее решение однородного уравнения, где , 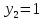. Находим частное решение неоднородного уравнения методом вариации постоянной, то есть:

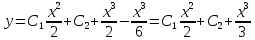
Это и будет общее неоднородное решение.

Системы линейных дифференциальных уравнений с постоянными коэффициентами.

Пусть имеется n неизвестных функций и n уравнений:

Данная система может быть сведена к системе первого порядка с помощью дополнительных функций:

После таких замен в системе (*) сократились только функции и их первые производные. После этого система (*) записывается в так называемом нормальном виде, когда все первые производные находятся слева:

Либо неизвестную обозначают t, а функцию – x(t):

Введём матричные обозначения:

Решение ищется в виде:

Лекция 16 (46) (20.12.10)

Из предыдущей лекции мы узнали, что однородные системы в нормальном виде записываются так:

Система (*) в векторно-матричном виде будет выглядеть так: .

Перейдём непосредственно к решению. Будем искать решение . Ищем решение системы в таком виде:

В матричном виде: или . Это собственный вектор матрицы.

1. Все n корней простые действительные числа: λ₁, λ₂, …, λ_n. Для λ₁ находим , для λ₂ находим и так далее. Если все λ_n – различные корни, то мы получим n линейно независимых векторов. Образуется ФСР – фундаментальная система решений.

Фундаментальной системой решений системы уравнений (*) называется системы из n линейно независимых вектор-функций.

– определитель Вронского.

2. Если какой-то корень λ оказался кратным (кратности k). Пусть λ₀ – корень характеристического уравнения кратности k, тогда решение надо искать в виде: (если при λ₀ система имеет m линейно независимых векторов).

3. Если λ₀ – комплексный корень характеристического уравнения.

– корень, – тоже корень.

и другое:

Общим решением системы (*) называется такая форма решений, в которой содержатся произвольные коэффициенты, что любое решение этой системы получается из общего решения при каком-то определённом наборе постоянных (теорема о структуре общего решения однородной системы).

Если есть ФСР, то , - некоторое произвольное решение системы (*).

Пример на однородную систему. , , :

Напишем характеристическое уравнение:

При :

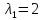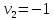Пусть , тогда и 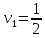, или, если умножить всё на 2, то , , . Получили решение для :

При (кратности 2):

В системе один линейно независимый вектор решения, следовательно, решение:

При t:

При свободных членах:

Пусть , , тогда:

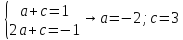
Пусть , , тогда:

ФСР:

Общее решение: .