Пример.
Если
,
то решение содержится в общем семействе
(при
).
Если
,
то решение добавляется к общему семейству.
Второй класс уравнений – однородные уравнения.
Определение
однородной функции.
Функция f(x,y)
называется однородной
функцией
своих переменных x
и y,
если, каково бы ни было число
,
выполняется следующее:
,
где p
– степень
(показатель) однородности.
Например,
– однородная функция, степень однородности
,
так как
.
Степень p
может быть равной нулю, если
.
Уравнение
называется однородным,
если функция, стоящая в правой части,
является однородной функцией своих
переменных.
Пусть
f(x,y)
будет однородной функцией степени 0, то
есть
.
Пусть
,
тогда
.
Уравнения такого типа решаются заменой
(переходом к новой функции):
.
– общее
решение.
Если
,
а
,
то:
Если
,
то уравнение
имеет корень u0,
тогда:
– решение:
– прямая
наряду с семейством.
Общий
вид однородного уравнения,
если его записать в
виде дифференциалов:
То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.
Пример.
Это
однородное уравнение. Решаем его заменой:
.
Третий класс уравнений – линейные уравнения.
Общий
вид
данных
уравнений:
Принцип
решения линейных уравнений.
Разделим на A:
Если
,
то это будет однородное уравнение:
Если
же
,
то применяется приём, называемый
вариацией постоянной:
Оно подставляется в неоднородное уравнение:
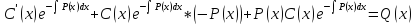
Окончательно неоднородное уравнение будет иметь вид:
Лекция 10 (40) (08.11.10)
Дифференциальные уравнения Бернулли.
Это
уравнения следующего вида:
Принцип решения:
Если
обозначить
за Z(x),
то
.
Отсюда
.
Подставим это выражение выше и получим:
Получили дифференциальное линейное уравнение, принцип решения которого рассмотрен выше.
Пример.
Это
уравнение Бернулли. Степень
.
Делим
на
:
Пусть
,
тогда
,
откуда
.
Подставим:
Находим общее решение соответствующего однородного уравнения:
Мы получили общее решение соответствующего однородного уравнения. Найдём частное решение неоднородного уравнения методом вариации постоянной:
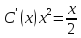
Дифференциальные уравнения Риккати.
Это уравнения следующего вида:
Если
известно хотя бы одно частное решение
этого уравнения, например y0(x),
то уравнение решается заменой:
.
Оно сводится к следующему:
Где y0 удовлетворяет исходному уравнению, а именно:
Поэтому все такие слагаемые уничтожаются, и получаем:
Получили дифференциальное уравнение Бернулли, принцип решения которого рассмотрен выше.
Уравнения в полных дифференциалах.
Это уравнения следующего вида:
Если
левая часть есть дифференциал некоторой
функции u(x,y):
– общий интеграл уравнения; если
,
а
,
то критерий
полного дифференциала
.
Предположим,
что критерий выполняется. Найдём эту
функцию u.
Пусть
,
тогда
.
Так как
,
то:
Отсюда находится φ'(y).
Пример.
Дифференциалы равны, значит это уравнение в полных дифференциалах.
Теперь интегрируем полученное выражение по переменной y и приравниваем к N:
Подставляем в (*), это и будет ответ:
Интегрирующий множитель.
Пусть уравнение
оказалось
НЕ уравнением в полных дифференциалах.
Возникает вопрос, существует ли функция
μ(x,y),
которая:
становится полным дифференциалом, где
μ
– интегрирующий
множитель.
Если
(*) имеет решение, то есть
(определяет y
как неявную функцию от x,
то есть y(x)),
то продифференцируем это по x.
Из равенства выше получаем:
Из
выражения
можно также записать, что
.
Отсюда
следует, что
и
.
Значит, всегда существует такой множитель
μ(x,y),
что
и
.
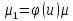
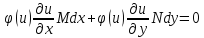
Пусть
.
Если
найдены два интегрирующих множителя
μ1
и μ,
то их отношение
.
Это и будет решение
уравнения без всяких квадратур.
Если μ(x,y) зависит только от x:
Пример.
Проверяем, умножив обе части на ex:
Это и есть решение.
Часто встречающиеся интегрируемые комбинации:
Лекция 11 (41) (15.11.10)
Пример
на подбор интегрирующего множителя.
Если
μ2
– интегрирующий множитель, то любая
функция
.
Возьмём
,
тогда
.
В итоге
.
Проверим:
Действительно:
Дифференциальные уравнения, не разрешённые относительно производной.
Это
уравнения такого вида:
.
Уравнения первого порядка n-ой степени решаются так:
Пример.
Первое
уравнение решается просто:
.
Второе уравнение – линейное. Сперва решается соответствующее однородное уравнение, то есть:
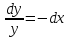
– это
общее решение однородного уравнения.
Найдём теперь частное решение неоднородного
уравнения
методом вариации постоянной:
Подставляем в неоднородное уравнение, получаем:
Окончательно получаем:
Если
из уравнения
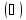y
можно выразить, то есть
,
то это решается методом введения
параметра, а именно:
Обозначим
,
получим:
Продифференцируем по x:
Получили
уравнение, разрешённое относительно
производной. p(x,C)
подставляем в (*), получим:
.
Это и будет решение.
Рассмотрим
теперь случай, когда из уравнения
можно явно выразить x,
то есть
.
Вводим параметр
,
получаем
.
Дифференцируем по y
обе части:
Мы
получили уравнение, разрешённое
относительно производной
.
В итоге получаем:
.
Пример.
Вводим
параметр
,
получаем:
Дифференцируем по y:
Запишем решение в параметрической форме:
Уравнение Лагранжа.
Это
уравнение, линейное относительно x
и y,
то есть оно имеет такой вид:
.
Принцип решения:
Вводим
параметр
,
получаем:
Пусть
,
поделим всё выражение на A(p):
Продифференцируем по x:
Получили
линейное уравнение первого порядка.
Отсюда находим
.
В итоге решение в параметрическом виде:
Отдельно
рассмотрим случай, когда
:
-
Если это тождество, то есть
,
то:
-
Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть
,
тогда
– решение.
Уравнение Клеро.
Частный
случай уравнения Лагранжа – это уравнение
Клеро.
Это когда уравнение Лагранжа имеет
следующий вид:
.
Принцип решения:
Вводим
параметр
,
получаем
.
Дифференцируем по x,
получаем:
Общее решение уравнения Клеро:
Здесь
– семейство
всевозможных кривых;
– огибающая
этого семейства,
тоже является решением и называется
особое
решение.
Пример
на уравнение Клеро.
Вводим
параметр
,
получаем:
.
Общее
решение:
.
Особое
решение (огибающая):
.
Лекция 12 (42) (22.11.10)
Теорема
существования решения дифференциального
уравнения первого порядка
вида:
(теорема
Пикара).
Если в уравнении (*) функция f(x,y) удовлетворяет следующим условиям:
f(x,y) непрерывна как функция двух переменных