Тройной интеграл.

Пусть в некоторой области (V) с границей (S) задана в каждой точке функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (V_i).

В каждой (V_i) возьмём произвольную точку (ξ_i, η_i, ζ_i) и составим интегральную сумму: . Устремим . Тогда, если существует предел интегральных сумм, то:

Мы получили формулу для вычисления объёма параллелепипеда.

Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед.

Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда:

Рассмотрим второй случай.

Рассмотрим третий случай – область (V) цилиндрического типа.

Пример. Вычислить тройной интеграл , где область V ограничена поверхностями , , , .

Нарисуем это тело. Область V представляет собой тетраэдр.

Лекция 07 (37) (18.10.10)

Формула Гаусса-Остроградского.

Рассмотрим тело (V) в пространстве с ограничивающей поверхностью (S).

Рассмотрим некую функцию R(x,y,z), заданную в области (V) и на границе, непрерывную в этой области и на границе вместе со своими частными производными первого порядка.

Рассмотрим интеграл . Воспользуемся первым способом и спроецируем тело на область D. Возьмём точку (x,y).

Складывая эти формулы, получаем формулу Остроградского-Гаусса:

Формула сводит интеграл от объёма к интегралу по границе.

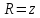Если и или и или и , тогда

А если , и , то:

Замена переменных в тройном интеграле.

Пусть имеется тело (V) с границей (S).

Пусть , тогда .

Замена:

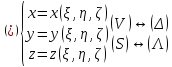
Преобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно:

Пусть поверхность (Λ) задаётся параметрически, то есть:

Получаем параметрическое задание поверхности (S):

Два последних двойных интеграла равны, так как:

Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу: .

Пусть , , , тогда:

Выражение в скобках равно нулю. Оставшееся выражение запишем так:

Это якобиан преобразования.

Окончательно получаем:

А для общего случая:

Цилиндрические координаты:

Переходим от координаты M(x,y,z) к M(ρ,φ,z). Это цилиндрические координаты, где:

Получаем, что .

Сферические координаты:

Получаем элемент объёма сферических координат: .

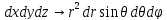Лекция 08 (38) (25.10.10)

Пример на замену переменных в тройном интеграле. Вычислить объём тела, ограниченного поверхностью .

Здесь симметрия: , , , .

Ответ: .

Элементы теории поля.

Пусть в каждой точке трёхмерного пространства задана скалярная функция .

Скалярное произведение двух векторов: .

Векторное произведение двух векторов:

Пусть задано скалярное поле. Предположим, что у него существуют частные производные в каждой точке: , ,. Производная функции U(x,y,z) по направлению . Пусть вектор – единичный вектор, тогда его координаты: .

Если , то , , где , , .

Выражение, полученное выше, есть скалярное произведение вектора и вектора .

– градиент.

Знак - это вектор Набла.

Из последнего выражения видно, что максимально, когда совпадает с направлением градиента. Следовательно, градиент показывает направление наибольшего изменения скорости функции.

– поверхность уровня функции .

Пример. . Найти градиент.

, где .

Введём понятие потока вектора через поверхность.

Распространение тепла. Пусть задано векторное поле в каждой точке пространства: .

Пусть в пространстве имеется температура U(M) как функция точки M.

Поток тепла через поверхность S за время t: , где k – коэффициент теплопроводности, dt – время.

Поток тепла в единицу времени:

Плотность потока тепла – количество тепла через единичную поверхность: .

Поток произвольного вектора 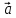через поверхность S: , так как .

Формула Гаусса-Остроградского в векторном виде. Пусть . В обычном виде формула выглядит так:

Левую часть можно записать и так: , , . Следовательно:

Мы получили поток вектора через замкнутую поверхность.

– это называется дивергенция или расходимость.

Формула Гаусса-Остроградского в векторном виде записывается так:

Поток вектора через замкнутую поверхность равен интегралу по объёму от его дивергенции.

Второе определение дивергенции. Возьмём некий малый объём V:

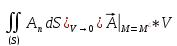
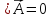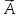Если дивергенция равна нулю, то есть , то поле вектора называется соленоидальным.

, поэтому поток везде, на каждом сечении трубки, одинаков.

Дивергенцию можно записать и с помощью оператора Набла: .

Перейдём к векторной записи формулы Стокса.

Это обычная формула Стокса.

– циркуляция вектора вдоль контура (L).

Векторная форма записи формулы Стокса:

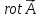- это ротор, или вихрь.

Ротор через оператор Набла можно записать так:

Если , то поле называется безвихревым или потенциальным.

Условие потенциальности поля – если , ; .

Второе условие потенциальности поля. Интеграл по любому замкнутому контуру равен нулю, значит, он не зависит от пути интегрирования.

Пример. Вычислить Набла от .

Лекция 09 (39) (01.11.10)

Дифференциальные уравнения.

Функция одной переменной y(x).

Дифференциальным уравнением называется соотношение , в котором x – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка.

Общий вид обыкновенного дифференциального уравнения n-ого порядка: .

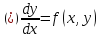– уравнение, разрешённое относительно производной.

f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.

Пусть . График функции называется интегральной кривой, – изоклины кривые.

Пусть правая часть уравнения (*) не зависит от y, то есть , тогда .

На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.

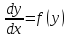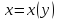Пусть . Будем считать независимой переменной y, а x – функция от y, то есть . Тогда . Но если и это уравнение имеет корень , то добавляется решение, которое надо добавить к общему семейству, зависящему от параметра C.

Всякая функция вида при подстановке в (*), после чего (*) становится тождеством, является решением (общим решением дифференциального уравнения (*)).

Если C взято равным конкретному числу, то решение φ(x,C₀) называется частным решением уравнения (*). - отсюда находится значение C.

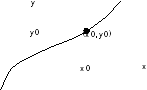
Условие Коши – когда указано, какому x₀ соответствует y₀. Задача Коши: – условие уравнения + условие Коши, то есть .

Пример. Дано: и . Решить задачу Коши.

Когда , то :

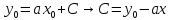
– частное решение задачи Коши.

Первый класс уравнений – уравнения с разделяющимися переменными.

Принцип решения таких уравнений:

Если дано условие Коши, то есть и , то:

Если и уравнение имеет корень , то это решение добавляется к основному семейству.