Поверхностные интегралы.

Рассмотрим пространство в некоторой области D плоскости xy с границей S. На области D переменных (x,y) задана поверхность (S): .

В каждой точке M этой поверхности задана функция . Некоторой сеткой кривых область D разбивается на частичные области D_i, в каждой частичной области берётся точка с координатами (x_i,y_i). Ей соответствует на поверхности точка M_i с координатами (x_i,y_i,z_i). Составляем интегральную сумму: , в каждой точке M_i проводим плоскость, проходящую через M_i и касательную к поверхности. Цилиндр, проходящий через D_i, вырезает плоский криволинейный четырёхугольник (T_i), где T_i – его площадь. Устремляем , тогда . Это и есть поверхностный интеграл первого рода. По теореме элементарной геометрии , где γ – угол между z и нормалью касательной плоскости. В следующей лекции найдём cos γ.

Лекция 05 (35) (04.10.10)

Проведём через точку M плоскость, перпендикулярную оси Y. Вид слева:

Проведём плоскость, перпендикулярную оси x. Она рассечёт по некоторой кривой плоскость.

Если взять их векторное произведение, то это будет нормаль к поверхности в точке M (x₀,y₀,z₀):

Отсюда следует, что и окончательно получим:

Мы получили формулу площади поверхности.

Пример. Найти площадь полусферы с центром в начале координат. Область D: круг

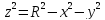
Вычислим площадь поверхности в более сложном случае: когда поверхность задана параметрически.

Вспомним, что такое полярные координаты:

Параметрическое задание кривой в пространстве:

Поверхность , где x и y – независимые переменные:

– это и называется параметрическое задание поверхности.

Вычислим площадь поверхности параметрически:

Поверхностный интеграл I-ого рода.

– задание поверхности.

Спроектируем S на плоскость xy, получим область D. Разобьём область D сеткой линий на части, называемые D_i. Из каждой точки каждой линии проведём параллельные z линии, тогда и S разделится на S_i. Составим интегральную сумму: . Устремим максимум диаметра D_i к нулю: , получим:

Это поверхностный интеграл первого рода

Так считается поверхностный интеграл первого рода.

При переходе от переменных x и y к u и v:

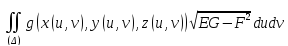
Поверхностный интеграл II-ого рода.

Введём понятие ориентированной поверхности и стороны поверхности.

Двусторонняя поверхность.

Проведём нормаль к точке M вверх.

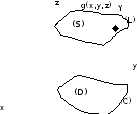
Лекция 06 (36) (11.10.10)

Формула Стокса.

Выведем формулу Стокса.

Пусть (S) – кусочно-гладкая поверхность, ограниченная (L). Рассмотрим интеграл вдоль границы (L): . Пусть поверхность (S) задана параметрически:

Так как , то:

В итоге получаем:

Рассмотрим теперь интеграл :

По аналогии запишем и третий интеграл и в итоге получим:

Это и есть формула Стокса. Она позволяет свести криволинейный интеграл к поверхностному интегралу. Проверим полученную формулу:

Формулу Стокса можно записать и так:

Мы записали поверхностный интеграл I-ого рода.

Следствия из формулы Стокса:

1. Криволинейный интеграл по замкнутому контуру, целиком принадлежащий односвязной области S, равен нулю, то есть , тогда и только тогда, когда , , . Назовём это условие (*).

2. Необходимым и достаточным условием того, что интеграл не зависит от пути интегрирования, является условие (*).

Необходимым и достаточным условием того, чтобы , является условие (*).