
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЕЧЕРНИЙ ФАКУЛЬТЕТ
2 Курс, 3 семестр
ПРЕПОДАВАТЕЛЬ
МИХАЙЛОВ ВЛАДИСЛАВ ДМИТРИЕВИЧ
СТУДЕНТ ГРУППЫ В03-121
НИКОЛАЕВ ВЛАДИМИР АЛЕКСАНДРОВИЧ
НИЯУ МИФИ, 2010 год.
Лекция 01 (31) (06.09.10)
Двойной интеграл.
Пример. Вычисление двойного интеграла как объёма тела цилиндрической формы.


Разбиваем
область D
сеткой, Di
– частичные области, M:
(ξi,
ηi).
 ,
где Di
– площадь частичной области. Увеличим
число частичных областей, измельчая их
добавлением новых линий разбиения, тем
самым увеличивая точность вычисления
объёма. Пусть λ
– характеристика
разбиения,
которая равна
,
где Di
– площадь частичной области. Увеличим
число частичных областей, измельчая их
добавлением новых линий разбиения, тем
самым увеличивая точность вычисления
объёма. Пусть λ
– характеристика
разбиения,
которая равна
 ,
где di
– диаметр частичной области. Диаметр
– максимальное расстояние между любой
парой точек в области. Устремим λ
к нулю. В пределе получаем точное
выражение для объёма:
,
где di
– диаметр частичной области. Диаметр
– максимальное расстояние между любой
парой точек в области. Устремим λ
к нулю. В пределе получаем точное
выражение для объёма:
 .
Это и есть двойной
интеграл.
.
Это и есть двойной
интеграл.
Предположим, что область D – прямоугольник.


Мы
знаем, что
 .
Это когда фигура выглядит примерно так:
.
Это когда фигура выглядит примерно так:

Возьмём произвольную точку x0 и построим сечение. Пусть площадь сечения в точке x0 равна Q(x0). Спроектируем на ось OY. Элементарный объём:



Так
как объём и есть двойной интеграл, то:

Замечание.
Ввиду симметрии:

Если в основании не прямоугольник:


Перейдём
к определению
двойного интеграла в общем случае.
Пусть на плоскости XY
задана функция
 и область (P)
(область задания функции f(x,y)),
её площадь P.
и область (P)
(область задания функции f(x,y)),
её площадь P.

Произведём
разбиение площади сеткой кривых Pi,
где Pi
–
частичная область. Внутри частичной
области возьмём произвольную точку с
координатами (ξi,ηi).
Составим интегральную сумму:
 .
Характеристику разбиения
.
Характеристику разбиения
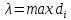 устремим к нулю. Если существует предел
интегральных сумм
устремим к нулю. Если существует предел
интегральных сумм
 ,
то этот предел и называется двойным
интегралом:
,
то этот предел и называется двойным
интегралом:
 .
.
Свойства интегральных сумм:
-
 на
частичной области (Pi),
на
частичной области (Pi),
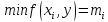 на частичной области (Pi),
можно ввести понятия нижней
и верхней
интегральных сумм (сумм
Дарбу):
на частичной области (Pi),
можно ввести понятия нижней
и верхней
интегральных сумм (сумм
Дарбу):
 – нижняя
интегральная сумма (сумма Дарбу).
– нижняя
интегральная сумма (сумма Дарбу).
 – верхняя
интегральная сумма (сумма Дарбу).
– верхняя
интегральная сумма (сумма Дарбу).
-
Если к линиям разбиений добавить конечное число линий разбиения, то s может только увеличиться, а S – уменьшиться.
-
Для любых разбиений
 ,
все нижние интегральные суммы ограничены
сверху, значит
,
все нижние интегральные суммы ограничены
сверху, значит
 – нижний
интеграл Дарбу.
Все верхние интегральные суммы ограничены
снизу, значит
– нижний
интеграл Дарбу.
Все верхние интегральные суммы ограничены
снизу, значит
 – верхний
интеграл Дарбу.
Можно записать так:
– верхний
интеграл Дарбу.
Можно записать так:
 .
.
Теорема.
Необходимое
и достаточное условие существования
двойного интеграла. Если
функция
 ,
заданная на области (P)
и ограниченная на ней, имеет интегральную
сумму
,
заданная на области (P)
и ограниченная на ней, имеет интегральную
сумму
 ,
а верхние и нижние интегральные суммы
s
и S,
то двойной интеграл
,
а верхние и нижние интегральные суммы
s
и S,
то двойной интеграл
 существует тогда и только тогда, когда
предел
существует тогда и только тогда, когда
предел
 (или в такой форме:
(или в такой форме:
 ,
где ωi
– колебание функции на частичной области
Pi,
где
,
где ωi
– колебание функции на частичной области
Pi,
где
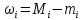 ).
Доказательство аналогично для однократного
интеграла.
).
Доказательство аналогично для однократного
интеграла.
Теорема. Непрерывная на области (P) функция f(x,y) интегрируема на ней.
Доказательство.
Берём ε>0.
Поскольку функция непрерывна, значит,
она равномерно непрерывна, то есть
существует такое δ>0,
что если взять любые две точки из любой
частичной области, диаметр которых d<δ,
то
 ,
следовательно,
,
следовательно,
 ,
ч.т.д. (
,
ч.т.д. ( ).
).
Теорема. Какие бы конечные значения не принимала функция f(x,y) на кривой L, двойной интеграл от этой функции на всей области P не меняется.

Доказательство. Пусть максимальное расстояние от кривой L до границы S равно некоторой величине δ1. Если при каких-то значениях функции на кривой L двойной интеграл существует, то кривую можно заключить в такие частичные области с достаточно малой характеристикой λ, чтобы площадь многоугольной области, охватывающей эту кривую, была бы меньше λ. Тогда Q<ε и:

Свойства определённого интеграла:
-
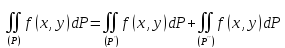 – свойство
аддитивности.
– свойство
аддитивности.

-
Свойства линейности:
а)

б)

-
Модуль интеграла меньше или равен интегралу от модуля:



Теорема
о среднем.
Так как
 ,
то, проинтегрировав это неравенство,
получим:
,
то, проинтегрировав это неравенство,
получим:



 ,
где
,
где
 .
.
