Предел функции

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как

или через символ предела функции:

Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике, геометрии, химии, теории вероятности и многим другим предметам.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

23.Правило Лопиталя

Предел функции, правило Лопиталя.

Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль  , бесконечность делить на бесконечность  .

К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность   и бесконечность минус бесконечновть  .

Дифференцирование функции и нахождение производной является неотъемлемой частьюправила Лопиталя, так что рекомендуем обращаться к этому разделу.

Формулировка правила Лопиталя cледующая:

Если  , и если функции f(x) и g(x) – дифференцируемы в окрестности точки  , то 

В случае, когда неопределенность не исчезает после применения правила Лопиталя, то его можно применять вновь.

Рассмотрим несколько примеров и подробно разберем решения.

Пример.

Вычислить предел, используя правило Лопиталя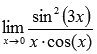 

Решение.

Подставляем значение

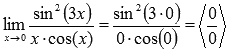
Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:

Ответ:

24.Первый и второй замечательные пределы

Первый замечательный предел

  Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере, при условии стремления этой дуги к нулю

.

  Непосредственное вычисление предела

приводит к неопределённости вида  .     Из геометрических соображений имеем S_DOAС< S_OAC < S_DOBC. Используя формулы площадей рассматриваемых фигур, получим

или

sin x < x < tg x

Разделив все части неравенства на sin x > 0, получим при условии х > 0

,

или

.

Так как функция у = cos x непрерывна, то

.

Пользуясь теоремой о пределе промежуточной функции, получим окончательно

.

  Замечание. Если х < 0, то знаки неравенств изменяются на противоположные, выводы же остаются прежними.

25.Частные производные функций нескольких переменных.

Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

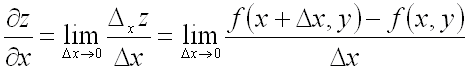Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Пусть задана функция   . Если аргументу   сообщить приращение  , а аргументу   – приращение  , то функция   получит приращение  , которое называется полным приращением функции и определяется формулой:  .

Функция  , полное приращение   которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно   и  , и величины бесконечно малой высшего порядка относительно  ):  , где   и   стремятся к нулю, когда   и   стремятся к нулю (т.е. когда  ), называется дифференцируемой в данной точке.

Линейная (относительно   и  ) часть полного приращения функции называется полным дифференциалом и обозначается  :  , где   и   – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям   и  .

26.Дифференцирование сложных функций.

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке  .

Пусть даны функции, определённые в окрестностях на числовой прямой,   где   и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

27. Дифференцирование неявных функций

Функция п переменных Называется неявной, если она задана

Уравнением

(18.17)

Не разрешенным относительно и.

Частные производные неявной функции, заданной уравнением (18.17), находятся по формулам

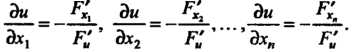
В частности, если - функция одной переменной Заданная

Уравнением , то

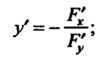(18.18)

Если г - функция двух переменных х, у, заданная уравнением , то

Если Где ,

То функция и называется сложной функцией независимых переменных . Переменные Назы

Ваются промежуточными аргументами.

Частная производная-сложной функции по одной из независимых переменных равна сумме произведений ее частных производных поцфомежуточным аргументам на частные производные этих аргументов по данной независимой переменной:

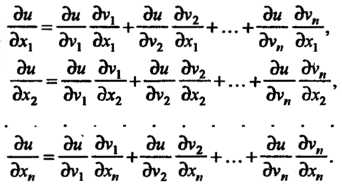
28.Общее решение дифференциального уравнения первого порядка с разделяющимися переменными.

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции.  Рассматривая производную y' как отношение дифференциалов  , перенесем dx в правую часть и разделим уравнение на h(y):

Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.  Обозначив  , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.  Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными.

29.Дифференциальные уравнения в частных производных.