3.2 . Элементы симметрии кристалла

Наличие пространственной трехмерной периодичности приводит к определенному ограничению вида общей операции симметрии кристалла(R,t), т.е. накладывает ограничения как на вид точечных операций R, так и на значения векторов трансляций t.

1. Набор операций чистых трансляций {(E,t_n)} является подгруппой пространственной группы {(R,t)}, поскольку среди операций пространственной группы по определению пространственной периодичности кристалла должны существовать элементы целочисленных трансляций. Если каждому узлу решетки кристалла с координатой x сопоставить тройку чисел n, т.е. писать x(n), то применение операции (R,t) переведет данный узел решетки в узел x(n), связанной с другой тройкой чисел n:

x(n)  (R,t)x(n)=Rx(n) + t

x(m)  (R,t)x(m)=Rx(m)+t

Поскольку x(n)–x(m)=t_p – целочисленный вектор трансляций, то и

t_q=x(n)–x(m)=[Rx(n)+t]–[Rx(m)+t]=R[x(n)–x(m)]=Rt_p ,

т.е t_q также целочисленный вектор трансляции. Таким образом,

Rt_p=t_q.

Это свойство приводит к тому, что группа трансляций (E,t_n) является подгруппой (R,t) с определенными свойствами. Ее сопряженные элементы со всеми элементами группы, не принадлежащими подгруппе трансляций (E,t), дают элементы из (E,t_p), т.е. сопряженная подгруппа совпадает с самой подгруппой. Такая подгруппа называется инвариантной подгруппой или нормальным делителем группы. Именно такова подгруппа трансляций {(E,t_n)} пространственной группы кристалла. Действительно,

(R,t)(E,t_n)(R,t)^–1=(R,t)(E,t_n)(R^–1,–R^–1t)=

(R,t)(R^–1,–R^–1t+t_n)=(E,–t+Rt_n+t)=(E,Rt_n)=(E,t_q).

2. Условие трехмерной периодичности также накладывает ограничения на операции R. Любой вектор x(n) может быть записан с помощью трех векторов элементарных трансляций a_i:

x(n)= a₁n₁+a₂n₂+a₃n₃

Однако его удобнее записать через декартовы (ортогональные) координаты основных векторов a_i:

Если применить операцию (R,t) к выражению x(n)–x(m)=t_p с учетом выражения x(n) через декартовые составляющие векторов трансляции, то получим

x(n)–x(m)=x(n)–x(m)=R[x(n)–x(m)]

Аn–Am=R[An–Am]

A[n–m]=RA[n–m]

Ap=Rap p=A^–1Rap

Вектор p и p – столбцы целых чисел. Поэтому элементы матрицы A^–1RA должны быть целыми числами, и характер преобразования A^–1RA, равный характеру матрицы R, должен быть целым числом. Но характер преобразования операции симметрии R равен 1+2cos. Следовательно 1+2cos равно целому числу. Единственными возможными значениями углов поворота  являются значения =2/n, где n=1,2,3,4,6. Поэтому в кристаллах единственно возможными поворотными осями могут быть оси порядка 1,2,3,4 и 6.

Ограничения, накладываемые на трансляции, можно получить, рассматривая повторение операции (R,t) m раз, где m – порядок операции R, т.е. R^m=E:

(R,t)^m=(R^m,(R^m–1+R^m–2+...+E)t)=(R^m,[R]t)

здесь обозначено, что [R]=R^m–1+R^m–2+...+E

Матрица преобразования R^m имеет вид:

Ясно, что если R^m=E, то полная операция группы (R,t)^m=(E,[R]t) должна быть чистой трансляцией, т.е. [R]t=t_n. Предположим, что t=t_p+_R, где

_R=а₁₁+a₂₂+a₃₃ (0<_i<1)

Поскольку [R]t_p=t_q, необходимо, чтобы [R]_R=t_n. Таким образом ясно, что помимо поворотов (первого и второго рода) и целочисленных трансляций t_n существуют операции нового вида – повороты и отражения с частичной трансляцией, обозначаемые символом (R,_R).

А. Плоскость зеркального скольжения. Пусть R=_z; тогда [R]=_z+E. Декартовы составляющие вектора частичной трансляции _R могут существовать лишь вдоль осей x,y, а составляющая вдоль z должна быть равна нулю, так как плоскость отражения перпендикулярна этому направлению z:

проекция по оси x : ₁а₁₁+₂а₁₂

проекция по оси y : ₁а₂₁+₂а₂₂

проекция по оси z : 0

Тогда

и должно выполняться [_z]_R=t_n:

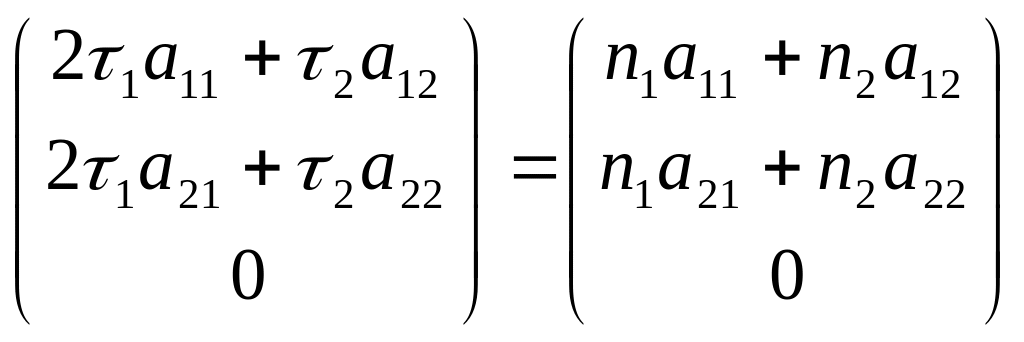
т.е.

2₁а₁₁+2₂а₁₂=n₁a₁₁+n₂a₁₂

2₁а₁₁+2₂а₁₂=n₁a₁₁+n₂a₁₂.

При (n₁,n₂)=(1,0) ₁=1/2;₂=0, т.е. вектор трансляции _R=a₁/2

при (n₁,n₂)=(0,1) ₁=0;₂=1/2, т.е. вектор трансляции _R=a₂/2

при (n₁,n₁)=(1,1) ₁=1/2;₂=1/2, т.е. вектор трансляции _R=(a₁+a₂)/2

Эти плоскости зеркального скольжения обозначаются соответственно a, b, и n. Кроме таких плоскостей зеркального скольжения в центрированных решетках могут быть плоскости с частичным скольжением и на 1/4 от целочисленных трансляций.

Таблица 9.