III. Небольшие программы

Для каждого из заданий этого раздела требуется написать программу вычисления некоторой величины по заданной формуле. Программу необходимо соответствующим образом оформить: пре­дусмотреть определение констант и описание переменных; исходные данные определить вводом; результаты напечатать.

III.1. Последовательная структура управления

1. (Вычисления по заданным формулам.)

а) Вычислить объем шара радиуса R по формуле .

б) Вычислить силу притяжения между телами массы m₁ и m₂, находящимися на расстоянии R друг от друга, по форму­ле , где  = 6.67340·10^-8 см²/г·сек² – гравитационная постоянная.

2. (Экономия переменных.) Вычислить:

a) ;

б) .

Указание. Новых переменных, отличных от x, y, z, u, не вводить. Использовать ограниченные арифметические вы­ражения, содержащие не более одной операции.

3. (Сохранение значений переменных.) Вычислить:

а) y = (x³–15.3x²)/(2.3–x)+3.4x³–x²;

б) y = (x⁵+5.7x³)/(x²–7.5)+4.2x⁵–8.9x².

4. (Оптимизация вычислений.) Вычислить:

а) y = x⁵⁹; б) u = v⁷¹w¹⁰³.

Указания. а) x⁵⁹ = x³²x¹⁶x⁸x²x (здесь 9 умножений, если запоминать промежуточные результаты). С другой сто­роны, x⁵⁹ = x³((((x³)²x)²)²)² (здесь 8 умножений – это лучшее, что можно придумать). б) Придумайте какой-нибудь быстрый способ вычисления u.

5. (Неявная постановка.) Вычислить:

а) точку пересечения прямых ax + by + c = 0 и dx + ey + f = 0 на плоскости;

б) коэффициенты произведения многочленов ax² + bx + c и gx + h.

6. (Схема Горнера.) Вычислить y = x⁵+3.4x⁴+2.8x³–5.7x²+x–1.1 по схеме y =  ((((x+3.4)x+2.8)x–5.7)x+1)x–1.1.

7. (Поиск закономерностей, или "развернутый цикл".) Вычислить:

а) у =  (x+4)+(x+4)(x+3)+ ... +(x+4)(x+3)(x+2)(x+1)x;

б) y =  (x+4)(1+(x+3)(1+(x+2)(1+(x+1))));

в) y = 1(1+x)(1+x+x²)(1+x+x²+x³)(1+x+x²+x³+x⁴);

г) y = 1²(1²+2²)(1²+2²+3²)(1²+2²+3²+4²)(1²+2²+3²+4²+5²).

8. (Приближенные формулы.) Вычислить:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Пояснение. "Двухэтажная" запись обозначает "многоэтажную" цепную дробь

.

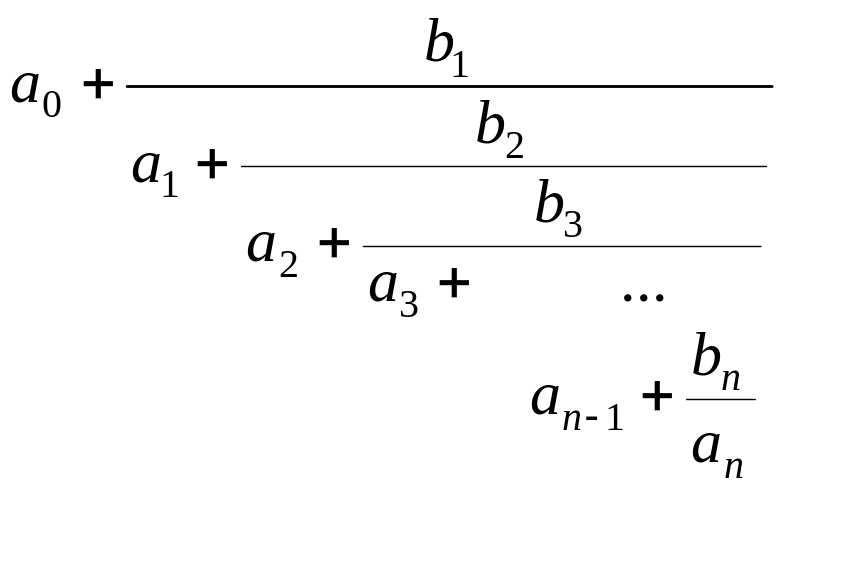9. (Использование стандартных функций.) Вычислить:

а) ;

в) ;

б) ;

г) .

Указание. Используйте следующие (предопределенные) стандартные арифметические функции: abs(x), sin(x), cos(x), exp(x), ln(x), sqrt(x) и arctan(x). Функций a^x и log_a x (ae) нет, но их можно выразить через exp(x) и ln(x).

III.2. Условная структура управления

N.B. Стандартную арифметическую функцию abs(x) для вы­числения |x| в этом подразделе не использовать!

10. (Отработка техники.) Вычислить:

a) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) , .

11. (Куча, или разное.)

а) Вычислить количество неотрицательных чисел среди x, y и z.

б) Вычислить число натуральных корней уравнения mx⁵ + nx = 15, где m, n – целые числа. (Указание: кор­нями могут быть только делители числа 15, т.е. 1, 3, ±5, ±15).

в) Переменной z присвоить значение true, если интер­вал [x, y] = U V (где U = [a, b], V = [c, d] – заданные интер­валы) не пуст, и значение false – в противном случае. (Указание: x=max{a, c}, y=min{b, d}; [x, y]   .)

г) Среди чисел k, l, т два одинаковых, а третье от­лично от них. Переменной n присвоить значение числа, отлич­ного от двух одинаковых.

д) Вычислить z – число действительных корней уравне­ния ax² + bx + c = 0 (a  0). Если z = 0, то вычислить сами корни x₁ и x₂ ; в противном случае положить x₁ = x₂ =0.

12. (Кусочно-заданные функции.) Вычислить:

a)

б)

в)

г)

д) , где

13. (Принадлежность области.) Переменной b присвоить значение true, если точка плоскости (х, y) принадлежит за­данной (замкнутой) области D, и значение false – в про­тивном случае. Варианты задания:

а) разрешается использовать булевские выражения общего вида;

б) разрешается использовать условные операторы, в состав которых входят только ограниченные булевские выраже­ния (отношения арифметических, имеющие вид А_°B , где _° обозначает символ отношения , , , > или , а A, В – арифметические выражения).

Варианты областей даны на рис. 3. Область D везде заштрихована. В вариантах к) – м) в D входят и линии, показанные жирно.

15. (Попадание в треугольник.) Установить, принадлежит ли заданная точка плоскости Е(x, у) замкнутой треугольной об­ласти с вершинами А(х₁, y₁), B(х₂, y₂), C(х₃, y₃).

Указание: E  ABC  |ABC| = |ABE| + |BCE| + |ACE|. Здесь |ABC| – площадь треугольника ABC. Отметим, что |ABC| = |x₁(y₂–y₃) + x₂(y₃–y₁) + x₃(y₁–y₂)| / 2.

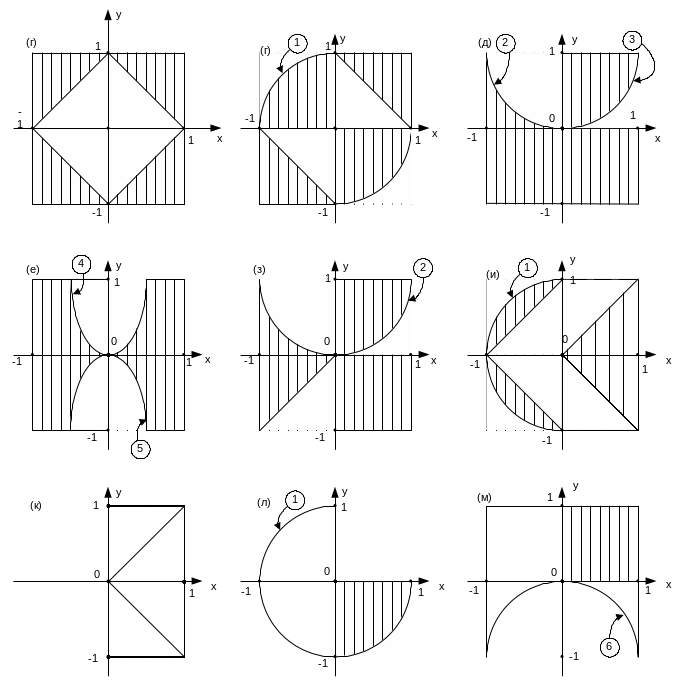
Рис. 3.

Уравнения границ: 1. x²+y² = 1; 2. y = x²; 3. x²+(y–1)² = 1; 4. y = 4x²; 5. y = –4x²; 6. y = –x². Остальные границы – прямые линии.